Presentazione di PowerPoint

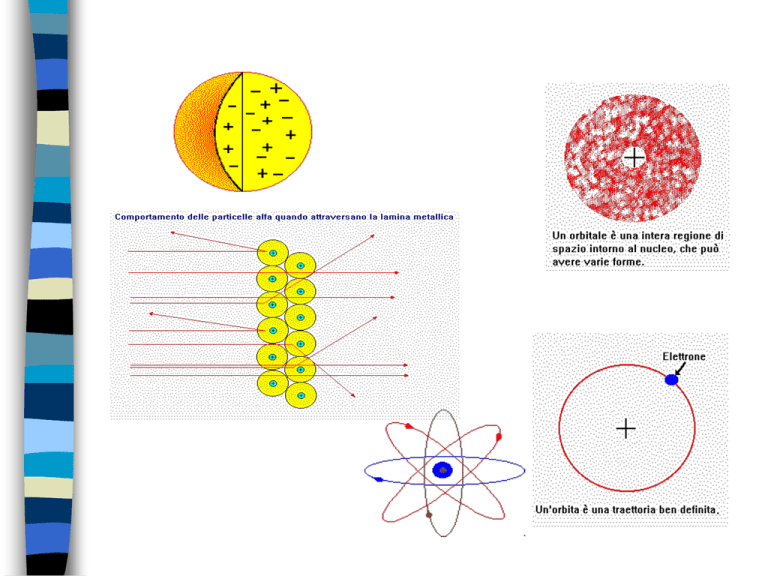
Atomo BOHR e quantizzazione
1)gli elettroni girano in orbite
circolari a raggio ben
definito
2) Il momento angolare
dell’elettrone è
quantizzato mvr= nh/2
3)l’elettrone non perde né
acquista energia quando si
trova nella stessa orbita.
L’energia di un quanto è
espressa dall’equazione di
planck
E=h h=cost di planck
= frequenza
C= =velocità luce
=C/
E=h E=mc2
h=mc2
Sostituzione di c con v(velocità generica)
h=mv2
=v/
hv/=mv2
mv2= hv
=hv/ mv2
=h/ mv Equazione di De Broglie
Una particella in movimento è associata ad un’onda
con prestabilita lunghezza e calcolabile conoscendo m e v
Heisenberg – Il principio di
indeterminazione di
Heisenberg afferma che non
si può conoscere nello stesso
istante la posizione e la
velocità dell’elettrone in
quanto esso ha una doppia
natura: particella e onda per
cui più è indeterminata la
posizione e più sarà
determinata la quantità di
moto
p xh
p= indeterminazione della
quantità di moto
x= indeterminazione della
posizione
DA ORBITA A ORBITALE=
SOLUZIONE DELLA FUNZIONE DI
STATO DI SCHRODINGER
NUMERI QUANTICI:
n
l
m
ms

Valori dei numeri quantici

n= da 0 a + indica il livello di E dell’elettr.

l= da 0 a n-1 la forma dell’orbitale.(dipende da n)

m = da –l; 0; +l l’orientamento nello spazio
dell’orbitale(dipende da l e quindi da n)

ms = numero quantico di spin (dall’ingl. To spin= ruotare).
Indica il verso di rotazione dell’elettrone

GLI ELETTRONI E DI CONSEGUENZA GLI ORBITALI
SONO GOVERNATI DA QUESTI NUMERI QUANTICI.

VALORI DEI NUMERI QUANTICI
n
l
m
Tipi di orbitali
1
0
0
1s •
2
0
1
0
-1,0+1
2s •
2p •••
3
0
1
2
0
-1,0+1
-2,-1,0,+1,+2
3s •
3p •••
3d •••••
4
0
1
2
3
0
-1,0,+1
-2,-1,0,+1,+2
-3,-2,1,0,+1,+2,+3
4s •
4p •••
4d •••••
4f •••••••
In ogni casella si inseriscono 2
elettroni rappresentati con 2
frecce una rivolta verso l’alto ed
una verso il basso
Configurazione elettronica:
 Regola di haufbau (gli elettroni
spontaneamente occupano gli stati quantici
disponibili a minor energia)
 Regola di hund (se più elettroni hanno lo
stesso contenuto energetico, essi tendono
a disporsi isolatamente nel maggior numero
di orbitali possibili, compatibili con
quell’energia.
 Principio di esclusione del Pauli (in un
orbitale possono esserci solo 2 elettroni a
spin opposto : campo elettrico/ campo
magnetico.

Applicazione regole
1s-2s-2p-3s-3p-3d-4s-4p-4d-4f
 s<p <d <f

P(x)
P(y) P(z)
Orbitali a stesso contenuto energetico