caratteristiche degli amplificatori

Spettro di frequenza dei segnali
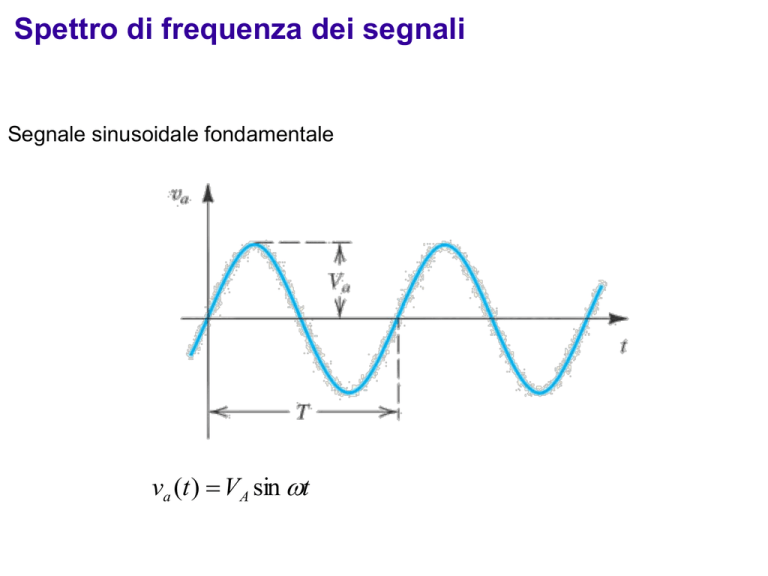
Segnale sinusoidale fondamentale
va (t )  VA sin t
Segnali periodici di forma arbitraria possono essere ottenuti come serie di
Fourier di segnali sinusoidali
0
4V 
1
1

sin

t

sin
3

t

sin
5

t




0
0
0
 
3
5

2
0 
frequenza fondamentale
T
v (t ) 
Spettro di frequenza: ampiezze delle sinusoidi della serie
0
Lo spettro consiste di frequenze discrete:
0 (frequenza fondamentale) e le sue armoniche
Segnali non periodici
Lo spettro consiste di frequenze è
continuo
0
Amplificazione del segnale
vO (t )
vI (t )
Linearità: vO (t )  AvI (t )
Guadagno:
Av 
vO
vI
caratteristica di
trasferimento
La necessità dell’amplificazione
Esempio: segnali prodotti da rivelatori di particelle
Spesso l’ampiezza (e la potenza) del
segnale è piccola
Stadio di amplificazione prima dell’ADC
Guadagno
• Guadagno di tensione:
Av 
vO
vI
• Guadagno di corrente:
iO
AI 
iI
• Guadagno di potenza:
AP 
iO vO
iI v I
Espressione del guadagno in decibel (dB)
• Guadagno di tensione (dB):
20 log | Av |
• Guadagno di corrente(dB):
20 log | AI |
• Guadagno di potenza(dB):
10 log AP
Un guadagno negativo non significa attenuazione
Il guadagno di potenza
Potenza fornita
dalle alimentazioni
Potenza del
segnale di output
Potenza dissipata in
calore dall’amplificatore
L’energia richiesta per per aumentare la potenza del segnale di ingresso viene
fornita dalle alimentazioni
Efficienza dell’amplificatore  
Pload
100
Pdc
Esempio
Saturazione
L = livelli di saturazione
= tensione di alimentazione
entro qualche V
picchi dell’output tagliati
a causa della saturazione
forma d’onda
di output
Dobbiamo avere
L
L
 vI 
Av
Av
forma d’onda
di input
Caratteristica di trasferimento non lineare e biasing
In generale la caratteristica di
trasferimento non è lineare su tutte le
tensioni di input
biasing attorno
a VI
vI (t )  VI  vi (t )
vO (t )  VO  vo (t )
vo (t )  Av vi (t )
dvO
Av 
dvI
Q
Esempio
Caratteristica di trasferimento di un transistor
vO (t )  10  1011 e 40vI
vI  0
vO  0.3
abbiamo L-=0.3, che corrisponde a vI=0.69 V. Il limite L+ è dato da
vI=0, L+=10-10-11 10 V
Modello di circuito per l’amplificatore di tensione
Input collegato
fra questi due
punti
Output
prelevato fra
questi due
punti
Analisi del primo stadio: è collegato un generatore di tensione reale modellato
cone un generatore ideale vs con in serie una resistenza Rs
partitore di tensione: ai capi di Ri appare solo una frazione di vs
Analisi del secondo stadio stadio: è presente un generatore di tensione
Avvi che amplifica vi
partitore di tensione: ai capi di RL appare solo una frazione di Avvi
Mettendo tutto assieme:
Av: guadagno di tensione dell’amplificatore ideale
Esempio: amplificatore a 3 stadi
Av1 
Av 2 
vi 2
100k
 10
 9.9 V/V
vi1
100k  1k
vi 3
10k
 100
 90.9 V/V
vi 2
10k  1k
vL
100
Av 3 
1
 0.909 V/V
vi 3
100  10
Av 
vL
 Av1 Av 2 Av 3  818 V/V
vi1
 58.3 dB
guadagno di corrente
vi1
1M

 0.909
vis 1M  100k
Ai 
io vL / 100


ii vi1 / 1M
 104 Av  8.18 106 A/A
vi1
vL vL vi1

 Av
vis vi1 vis
vis
 818  0.909  743.6 V/V
 57.4 dB
guadagno di potenza
PL vLio
AP 

 Av Ai
PI vi1ii
 818  8.18 106  66.9 108 W/W
 98.3 dB
L’amplificatore di corrente
un amplificatore di corrente dovrebbe avere:
• Ri = 0 (resistenza di input)
• Ro=  (resistenza di output)
Risposta in frequenza
Misura della risposta in frequenza
con un input sinusoidale
vi=Visin t
vo=Vosin (t+)
Vo
T ( ) 
Vi
 T ( )  
3bB
Reti STC (Single Time Constant)
Analisi del filtro passa-basso nel dominio delle
frequenze
segnali in notazione complessa
Legge di Ohm generalizzata v(t) = Z i(t)
Grafici di Bode
T ( ) 
1
1  ( / 0 )2
Filtro passa-basso
3dB 0 = 1/RC
20log T () (dB)
 / 0
scala log

   tan
 3dB
1
vo  vi
 vi
ZC
ZC  Z R
1
1  jRC
Grafici di Bode del filtro passa-alto
T ( ) 
1
1  ( 3dB /  ) 2
Filtro passa-alto
3dB = 1/RC
  tan 1
3dB

vo  vi
 vi
ZR
ZC  Z R
1
1  j 3dB / 
Risposta in frequenza di un amplificatore di
tensione
Vi  Vs
lato input

lato output
Ri || Z C
RS  Ri || Z C
1
1
1  RS / Ri 1  jC RS Ri /( RS  Ri )
RL
Vo  Vi
RL  RO
Risposta in frequenza di un amplificatore di
tensione
Il modello di amplificatore di tensione ha una risposta un frequenza ideale:
Vo/Vi non dipende da
Negli amplificatori reali sono presenti componenti capacitive che modificano la
risposta
Possibile
comportamento
tipo filtro passabasso
Un semplice modello consiste nell’introdurre un capacitore C in parallelo con la
resistenza di input Ri
Analisi della parte sinistra
senza capacitore (vecchia analisi)
col capacitore (nuova analisi)
Vo
1
1
1

VS
1  RS / Ri 1  Ro / RL 1  jC RS Ri /( RS  Ri )
Il guadagno dc (=0) è
K
Vo
1
1
(  0)  
VS
1  RS / Ri 1  Ro / RL
Abbiamo dunque una risposta tipo passa-basso
Vo
1
K
VS
1  j /  3dB
 3dB 
1
C ( Rs || Ri )
(riducendo VS a zero, vediamo subito che la resistenza vista da C è Rs||Ri)
Esempio
Poniamo Rs=20 k, Ri=100k , Ci=60 pF, =144 V/V, Ro=200 ,
RL=1 k.
Calcoliamo:
• il guadagno dc
• la frequenza a cui il guadagno diventa 0 dB
• la frequenza 3 dB
Classificazione degli amplificatori
Esempio di risposta in frequenza (amplificatore audio)
Discesa ad alta
frequenza dovuta a
capacità interne
come nel modello
Discesa ad bassa
frequenza?
Potrebbe essere dovuta a un capacitore
posto fra due stadi di amplificazione
(coupling capacitor)
Spesso è importante mantenere il guadagno anche a basse frequenze
 Amplificatori dc-coupled
Risposta in frequenza tipo filtro passa-basso
Amplificatori passa-banda