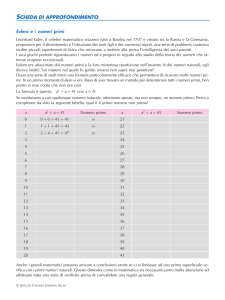
La geometria delle
trasformazioni
Summer school 2007
Politecnico di Milano
Emanuele Munarini
Contenuti della lezione
Il programma di Erlangen
Gruppi di trasformazioni
Geometrie del piano
Geometria proiettiva
Un modello del piano proiettivo reale
Sezioni coniche
Topologia
Deformazioni continue
Superfici topologiche
Classificazione delle superfici chiuse connesse
Il programma di Erlangen
Geometria e trasformazioni
Programma di Erlangen
(Felix Klein, 1872)
La geometria è lo studio delle proprietà invarianti
rispetto ad un gruppo di trasformazioni.
Le proprietà geometriche delle figure non sono
determinate dalla forma della figura ma dalle
trasformazioni che possono agire su di essa.
Geometria del piano
p : piano della geometria elementare
figura piana: un qualsiasi sottoinsieme del piano
(punti, rette, triangoli, rettangoli, circonferenze,
dischi, etc.)
trasformazione piana: una qualunque funzione
biunivoca T : p p.
Composizione di trasformazioni
Date due trasformazioni piane
T1 : p p e T2 : p p
la trasformazione composta è la funzione
T2 T1 : p p
definita applicando prima T1 e poi T2, ossia ponendo
(T2 T1)(P) = T2(T1(P))
per ogni punto P del piano p.
La composizione di due funzioni biunivoche è
ancora una funzione biunivoca
Quindi, la composizione di due trasformazioni
piane è ancora una trasformazione piana.
L’insieme S(p) di tutte le trasformazioni del piano
p è chiuso rispetto alla composizione (e possiede
una struttura di gruppo).
Struttura di gruppo di S(p)
la composizione è un’operazione interna;
la composizione è un’operazione associativa:
T1 (T2 T3) = (T1 T2) T3
esiste un elemento neutro, la funzione identità E :
p p, P P, tale che
TE=ET=T
esistono le trasformazioni inverse: per ogni
trasformazione T esiste una trasformazione inversa
T-1 tale che
T T-1 = T-1 T = E.
Figure piane equivalenti
Due figure piane F1 ed F2 sono equivalenti, o
congruenti, se esiste una trasformazione piana T
che porta la prima figura nella seconda, ossia se
F2 = T(F1).
In questo modo abbiamo definito una relazione tra
le figure del piano che generalizza la relazione di
uguaglianza. Più precisamente questa relazione è
una relazione di equivalenza.
Relazioni di equivalenza
riflessività: ogni figura è equivalente a sé stessa;
simmetria: se una figura F1 è equivalente ad una
figura F2 allora anche la figura F2 è equivalente
alla figura F1;
transitività: se una figura F1 è equivalente ad una
figura F2 e la figura F2 è a sua volta equivalente ad
una figura F3 allora la figura F1 è anch’essa
equivalente alla figura F3.
Geometrie piane
Dare una geometria piana significa assegnare un
sottogruppo G di S(p) delle trasformazioni
ammissibili.
La geometria è lo studio delle proprietà che
restano immutate comunque si applichi una delle
trasformazioni ammissibili. Ossia una proprietà
geometrica di una figura piana F è una proprietà
che vale per F e per ogni altra figura T(F) che si
può ottenere da F mediante una trasformazione
piana T appartenente al gruppo G.
Classificazione
Due figure piane F1 ed F2 sono equivalenti, o
congruenti, se esiste una trasformazione piana T
appartenente al gruppo G che porta la prima figura
nella seconda: F2 = T(F1).
Affinché questa relazione sia una relazione di
equivalenza occorre che G sia un gruppo.
Classificare le figure significa determinare le
classi di equivalenza, ossia i tipi di figure.
Geometria euclidea metrica
Supponiamo che p sia dotato di un’unità di misura
e quindi di una distanza d(P,Q) tra i punti.
Una isometria è una trasformazione T : p p
che conserva le distanze, ossia tale che
d(T(P),T(Q)) = d(P,Q)
per ogni punto P e Q del piano.
Esempi: traslazioni, rotazioni, simmetrie.
Figure invarianti: rette, rette parallele, rette
perpendicolari, triangoli, circonferenze.
Proprietà invarianti: lunghezze, aree, angoli.
Geometria euclidea simile
Una similitudine è una trasformazione T : p p
che conserva i rapporti tra le distanze.
Esempi: traslazioni, rotazioni, omotetie.
Proprietà invarianti: rapporti tra le distanze,
parallelismo tra rette, ampiezza degli angoli,
rettangoli, il teorema di Pitagora.
Proprietà non invarianti: lunghezze, aree.
Le isometrie sono particolari similitudini (quelle
per cui il rapporto delle desianze è 1). Allora ogni
proprietà simile è anche una proprietà metrica.
Geometria affine
Una affinità è una trasformazione T : p p che
conserva le rette, ossia l’allineamento dei punti.
Proprietà invarianti: parallelismo di rette,
congruenza tra segmenti, ellissi, le mediane di un
triangolo si intersecano in un unico punto .
Proprietà non invarianti: lunghezze, angoli,
rapporti tra distanze, circonferenze, rettangoli.
Le isometrie e le similitudini sono affinità.
Geometria proiettiva
La geometria delle proiezioni
o delle ombre
Proiezioni
p1 e p2: piani nello spazio ordinario
P: punto esterno a p1 e p2.
Proiezione: trasformazione T : p1 p2 definita in
modo che T(A) = B = PA p2:
Punti impropri
Per avere una corrispondenza biunivoca tra i due
piani bisogna aggiungere dei nuovi punti, detti
punti impropri o all’infinito. I punti all’infinito di
un piano formano una retta detta retta impropria.
I punti all’infinito del piano p1 sono quelli che
vengono mandati nella retta che si ottiene
intersecando il piano p2 con il piano p' parallelo a
p1 e passante per il punto P.
Geometria proiettiva
Una proiettività è una trasformazione che si
ottiene componendo un numero finito di
proiezioni e di sezioni.
Proprietà invarianti: rette, coniche, birapporto.
Le proiettività non conservano i punti all’infinito,
ossia possono portare un punto proprio in un
punto all’infinito e viceversa.
Le affinità del piano coincidono con le proiettività
che conservano la retta impropria.
Un semplice modello del
piano proiettivo reale
La geometria elementare nell’usuale piano
euclideo reale E2 è determinata dai seguenti
assiomi fondamentali riguardanti l’incidenza
tra punti e rette.
E1) per due punti distinti passa una ed una
sola retta;
E2) due rette distinte si intersecano
esattamente in un punto oppure non hanno
punti in comune.
Problema: gli assiomi E1 ed
E2 non sono simmetrici.
Più precisamente si ha, per così dire, un
difetto nell’assioma E2: le rette parallele non
hanno punti in comune.
Tuttavia anche due rette parallele hanno
qualcosa in comune: la direzione.
Questo diventa il punto di partenza per
rimediare al difetto degli assiomi euclidei.
Si amplia il piano euclideo ordinario
introducendo un nuovo tipo di punti, i punti
all’infinito.
Il piano esteso
i punti sono dati
da tutti i punti del piano euclideo E2, che verranno
chiamati punti propri, e
da tutte le direzioni in esso contenute, che verranno
chiamate punti impropri, o punti all’infinito;
le rette sono date
da tutte le rette del piano euclideo E2, che verranno
chiamate rette proprie, e
da una nuova retta r formata da tutti i punti impropri,
che verrà chiamata retta impropria o retta all’infinito.
Una nuova geometria
Chiameremo piano proiettivo P2 l’insieme
formato dai punti e dalle rette che abbiamo
appena introdotto.
Vediamo ora in che modo si modificano i
due assiomi E1 ed E2 che definivano la
geometria euclidea nel piano. L’assioma E1
continuerà a valere ma l’assioma E2
cambia, semplificandosi.
Per due punti distinti passa
una ed una sola retta.
Dimostrazione. Siano P e Q due punti distinti.
Se P e Q sono propri, per l’assioma E1 esiste
esattamente una retta propria che passa per essi.
Se P è proprio e Q è improprio allora esiste esattamente
una retta propria che passa per P e che ha la direzione
data da Q (quinto postulato di Euclide). Lo stesso vale
se P è improprio e Q è proprio
Se P e Q sono entrambi punti impropri, allora
appartengono alla retta impropria. Inoltre non possono
appartenere ad una stessa retta propria perché sono
distinti ed ogni retta propria ha esattamente un punto
improprio (che coincide con la sua direzione).
Due rette distinte si intersecano
esattamente in un punto.
Dimostrazione. Siano r ed s due rette distinte.
Se r ed s sono entrambe proprie, per l’assioma E2
hanno esattamente un punto proprio in comune (e
chiaramente non possono avere alcun punto improprio
in comune) oppure non hanno punti propri in comune
ma allora hanno esattamente un punto improprio in
comune (la loro direzione).
Se una delle due rette è propria e l’altra è impropria,
allora hanno in comune esattamente il punto improprio
che da la direzione della retta propria.
Rappresentazione
del piano proiettivo
A livello intuitivo possiamo rappresentare il piano
proiettivo come un disco il cui bordo rappresenta
la retta impropria, dove i punti del bordo
antipodali sono da considerarsi uguali tra di loro:
Sezioni coniche
Classificazione euclidea e affine
delle coniche
Dal punto di vista euclideo le coniche
irriducibili sono le ellissi, le parabole e le
iperboli.
Dal punto di vista affine c’è una sola ellisse,
una sola parabola ed una sola iperbole.
Cosa accade dal punto di vista proiettivo?
Coniche nel piano proiettivo
C’è una sola conica irriducibile, ossia tutte le
coniche irruducibili sono proiettivamente
equivalenti.
Topologia
La geometria
delle deformazioni continue
Nascita della topologia:
i ponti di Königsberg
E’ possibile attraversare tutti e sette i ponti
esattamente una volta e tornare al punto di
partenza?
Risposta: No (Eulero, 1736)
Deformazione continua
Equivalenza topologica
Trasformazioni continue
Una deformazione continua è una trasformazione
che porta punti vicini in punti vicini.
E’ lecito: tirare, torcere, piegare.
E’ proibito: tagliare, lacerare, strappare, bucare.
Un omeomorfismo del piano è una trasformazione
T : p p continua tale che anche la sua inversa
sia continua.
Topologia
La topologia è la geometria delle deformazioni
continue.
Le proprietà topologiche sono le proprietà che
restano invariate per deformazioni continue.
Proprietà topologiche: essere connessi ( cioè
essere fatti di un solo pezzo), possedere dei buchi,
avere un bordo, essere orientabili, ...
Proprietà non topologiche: distanze, lunghezze,
aree, parallelismo, ortogonalità, allineamenti, …
Superfici topologiche
Una superficie è una figura dello spazio in cui
ogni punto è circondato da una regione
topologicamente equivalente ad un disco.
Può essere utile pensare le superfici topologiche
come se fossero oggetti perfettamente elastici che
possono essere piegati, tirati, compressi o ritorti a
piacere purché non si verifichino strappi,
lacerazioni o tagli.
Si può anche tagliare e ricucire, purché nel
ricucire il taglio i punti originariamente vicini
tornino ad essere vicini.
Esempi di deformazioni
Disco e cilindro
Sfera
Toro
Toro a due buchi e a tre buchi
Bottiglia di Klein
Piano proiettivo reale
Figure che non sono
superfici topologiche
Superfici chiuse connesse
Le superfici possono avere un bordo (disco,
cilindro) oppure possono essere senza bordo
(sfera, toro).
Una superficie è chiusa quando è senza bordo,
come la sfera ed il toro. Il disco ed il cilindro non
sono superfici chiuse.
Una superficie connessa è una superficie formata
da un solo pezzo. Dischi, sfere, tori, bottiglie di
Klein, piani proiettivi reali e cilindri sono tutte
superfici connesse.
Superfici orientabili
Intuitivamente le superfici orientabili sono quelle
che hanno due facce (una “interna” ed una
“esterna” se chiuse), come la sfera, il toro, il disco
ed il cilindro.
In questo caso una ipotetica formichina posta su
una delle due facce non può passare sull’altra
faccia senza fare buchi (e senza attraversare il
bordo).
Superfici non orientabli
Benché le superfici orientabili siano quelle più
note ed intuitive, esistono anche superfici non
orientabili, ossia con una sola faccia.
Questo significa che la nostra ipotetica formichina
può percorrere tutta quanta la superficie senza mai
dover fare dei buchi (e senza mai dover
oltrepassare il bordo).
Nastro di Möbius (1858)
Non orientabilità
del nastro di Möbius
M. C. Escher, Möbius Strip II (Red Ants), 1963.
Bordo del nastro di Möbius
Il bordo del nastro di Möbius è una circonferenza.
Superfici non orientabili
Una superficie non è orientabile quando
contiene un nastro di Möbius.
Le bottiglie di Klein e i piani proiettivi reali
sono esempi di superfici chiuse non
orientabili.
Quindi, come vedremo, esse contengono un
nastro di Möbius.
Sviluppo piano del tetraedro
Costruzione delle superfici
chiuse: poligoni fondamentali
I poliedri possono essere sviluppati nel piano dopo
aver effettuato opportuni tagli lungo alcuni lati.
Anche le superfici chiuse connesse possono essere
rappresentate mediante opportuni sviluppi piani.
Ogni superficie chiusa connessa può essere
costruita a partire da un poligono orientato con un
numero pari di lati identificando a due a due i suoi
lati.
Tale poligono è detto il poligono fondamentale
della superficie.
Alcuni poligoni fondamentali
Identificando i lati etichettati con le medesime
lettere, rispettando la direzione delle frecce, si
ottengono rispettivamente:
la sfera
il toro
il piano proiettivo reale
la bottiglia di Klein
Costruzione della
bottiglia di klein
Non orientabilità della
bottiglia di Klein
Teorema Il piano proiettivo reale si può ottenere
incollando, lungo il bordo, un disco ed un nastro
di Möbius.
Dimostrazione: Rimovendo un disco da un piano
proiettivo reale si ottiene un nastro di Möbius:
Teorema La bottiglia di Klein si può ottenere
incollando due nastri di Möbius lungo il bordo.
Dimostrazione. Si considerino due nastri di
Möbius. Dopo aver identificato il bordo dei due
nastri (indicando con a e con b i due lati opposti),
tagliamo il primo nastro lungo il suo asse.
Incollando tra di loro i lati contrassegnati con a e
con b si ottiene il poligono che rappresenta una
bottiglia di Klein. Ossia
Somma connessa di superfici
La somma connessa di due superfici S1 e S2
è la superficie S1 # S2 che si ottiene
rimovendo un disco da entrambe le
superfici ed incollandole lungo il bordo dei
due dischi rimossi.
Ad esempio la somma connessa di due tori
è un toro a due buchi:
Proprietà della somma connessa
Commutatività:
S1 # S2 = S2 # S1.
Associatività:
(S1 # S2 ) # S3 = S1 # (S2 # S3 ).
Esistenza dell’elemento neutro:
S#S=S#S=S
dove S è la sfera.
Somma connessa con un toro
o con un piano proiettivo reale
La somma connessa di due tori è un toro a due
manici (con due buchi):
La somma connessa di una superficie S con un
toro T può essere pensata come la superficie S alla
quale si attacca un manico.
Se S è orientabile allora anche S # T è orientabile.
Somma connessa
con un piano proiettivo reale
La somma connessa di una superficie S con un un
piano proiettivo reale può essere pensata come la
superficie S alla quale si attacca una cross-cup.
S # P non è mai orientabile.
Somma connessa di due
piani proiettivi reali
Teorema La somma connessa di due piani
proiettivi è una bottiglia di Klein.
Dimostrazione. Rimovendo un disco da due piani
proiettivi ed incollando i due poligoni lungo il
bordo del disco rimosso si ottiene una bottiglia di
Klein.
Classificazione delle superfici
chiuse connesse I
Teorema (Deh - Heergaard, 1907) Ogni
superficie chiusa e connessa S dello spazio
ordinario è topologicamente equivalente
alla somma connessa di g tori:
S = T # # T = T#g (g 0)
se è orientabile; (se g = 0, S è una sfera S);
alla somma connessa di k piani proiettivi reali:
S = P # # P = P#g (k 1)
se non è orientabile.
Poliedri
Un poliedro è una figura geometrica
delimitato da poligoni, dette facce, che si
incollano lungo i lati, detti spigoli. Gli
spigoli si intersecano nei vertici.
Esempi: prisma, piramide.
Poliedri regolari
Un poliedro è regolare quando tutte le facce sono
poligoni regolari e uguali.
Esempi: tetraedro, cubo, ottaedro, dodecaedro,
icosaedro.
Caratteristica di Eulero
La caratteristica di Eulero di un poliedro P è il
numero
c(P) = V – S + F
dove V è il numero dei vertici, S è il numero degli
spigoli ed F è il numero delle facce di P.
Teorema (Formula di Eulero) Per ogni poliedro P
semplicemente connesso (cioè senza buchi) la
caratteristica di Eulero è data da c(P) = 2.
Caratteristica di Eulero del cubo
V=8
S = 12
F=6
c(Q) = V – S + F
= 8 – 12 + 6
=2
Poliedri regolari
Teorema Esistono solo cinque poliedri regolari:
il tetraedro (V = 4, S = 6, F = 4, c = 2)
il cubo o esaedro (V = 8, S = 12, F = 6, c = 2)
l’ottaedro (V = 6, S = 12, F = 8, c = 2)
il dodecaedro (V = 20, S = 30, F = 12, c = 2)
l’icosaedro (V = 12, S = 30, F = 20, c = 2)
Caratteristica di Eulero di una
superficie chiusa
La caratteristica di Eulero di una superficie chiusa
S è definita come la caratteristica di Eulero di una
qualunque superficie poliedrale topologicamente
equivalente a S.
Si dimostra che la definizione è ben posta, ossia
che c(S) non dipende dalla superficie poliedrale
utilizzata per calcolarla.
Caratteristica di Eulero del toro
V = 16
S = 32
F = 16
c(T) = V – S + F
= 16 – 32 + 16
=0
Caratteristica di Eulero
di alcune superfici
Disco: c(D) = 1
Cilindro: c(C) = 0
Nastro di Möbius: c(N) = 0
Sfera: c(S) = 2
Toro: c(T) = 0
Piano proiettivo reale: c(P) = 1
Bottiglia di Klein: c(K) = 2
Caratteristica di Eulero
di una somma connessa
Teorema La caratteristica di Eulero di una somma
connessa S1 # S2 è data da
c(S1 # S2) = c(S1) + c(S2) – 2.
Per la somma connessa di k superfici si ha
c(S1 # # Sk) = c(S1) + + c(Sk) – 2(k-1).
Se S1 = = Sk = S si ha
c(S # # S) = k c(S) – 2(k-1).
Caratteristica di Eulero delle
superfici chiuse e connesse
Per la sfera e per il toro si ha
c(S) = 2 e c(T) = 0.
Quindi per le superfici chiuse orientabili:
c(T#g) = g c(T) – 2(g-1) = 2 – 2 g
Per il piano proiettivo reale si ha
c(P) = 1.
Quindi per le superfici chiuse non orientabili:
c(P#k) = k c(P) – 2(k-1) = k – 2 k + 2 = 2 – k
Caratteristica di Eulero di una
superficie chiusa connessa
Teorema Per ogni g 0 e per ogni k 1 si
ha
c(T#g # P#k) = 2 – 2 g – k.
Dimostrazione
c(T#g # P#k) = c(T#g) + c(P#k) – 2
=2–2g+2–k–2
= 2 – 2 g – k.
Classificazione delle superfici
chiuse e connesse II
Teorema Le superfici chiuse e connesse sono
completamente caratterizzate, a meno di
omeomorfismi, dalla caratteristica di Eulero e
dall’orientabilità.
Le superfici chiuse orientabili hanno sempre
caratteristica di Eulero pari (c(T#g) = 2 – 2 g).
Le superfici chiuse con caratteristica di Eulero
dispari sono non orientabili: P # T # # T.
Le superfici non orientabili con caratteristica di
Eulero pari, sono: K # T # # T.
Esempio 1
Che superficie si ottiene dalla somma connessa di
un toro e di un piano proiettivo reale?
Si ha una superficie non orientabile T # P con
caratteristica c(T # P) = c(T) + c(P) – 2 = -1.
Ma c(P # P # P) = 3 c(P) – 4 = 3 – 4 = - 1.
Quindi la superficie T # P è topologicamente
equivalente alla somma connessa di tre piani
proiettivi reali, ossia
T # P = P # P # P.
Esempio 2
Che superficie si ottiene dalla somma connessa di
una bottiglia di Klein con un piano proiettivo
reale?
Si ha una superficie non orientabile con
caratteristica c(K # P) = c(K) + c(P) – 2 = -1.
Quindi si ha K # P = P # P # P.
Di conseguenza T # P = K # P, anche se il toro e la
bottiglia di Klein non sono topologicamente
equivalenti.
Fine