Funzioni goniometriche

Funzioni goniometriche
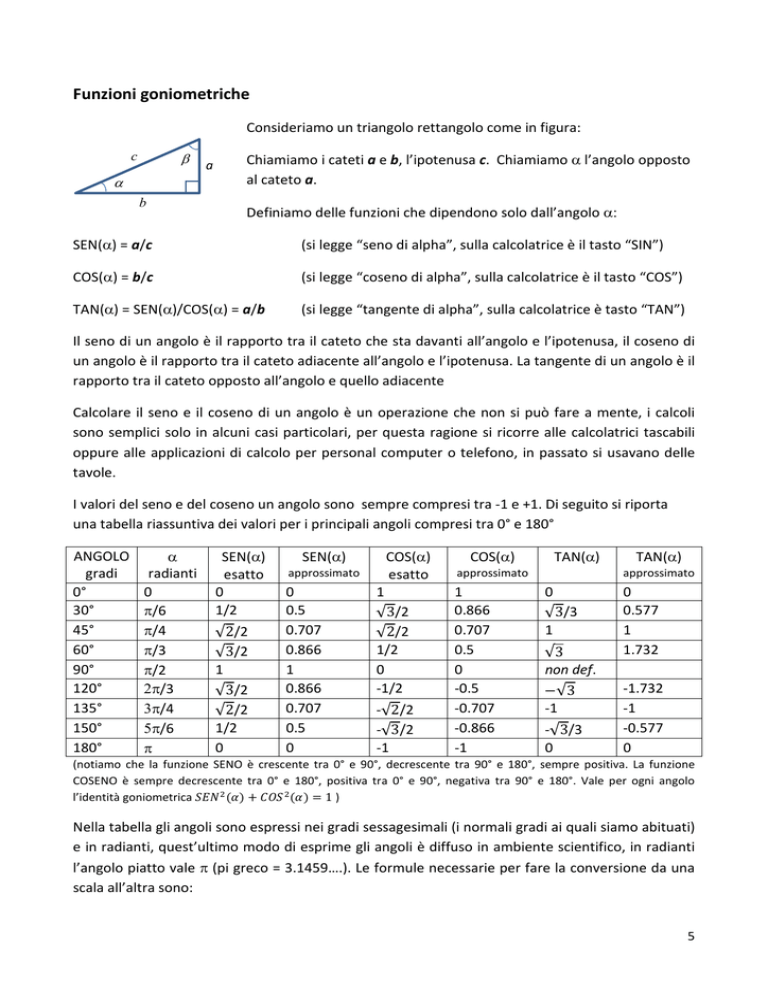
Consideriamo un triangolo rettangolo come in figura:
c
β
α
b
a
Chiamiamo i cateti a e b, l’ipotenusa c. Chiamiamo α l’angolo opposto
al cateto a.
Definiamo delle funzioni che dipendono solo dall’angolo α:
SEN(α) = a/c
(si legge “seno di alpha”, sulla calcolatrice è il tasto “SIN”)
COS(α) = b/c
(si legge “coseno di alpha”, sulla calcolatrice è il tasto “COS”)
TAN(α) = SEN(α)/COS(α) = a/b
(si legge “tangente di alpha”, sulla calcolatrice è tasto “TAN”)
Il seno di un angolo è il rapporto tra il cateto che sta davanti all’angolo e l’ipotenusa, il coseno di
un angolo è il rapporto tra il cateto adiacente all’angolo e l’ipotenusa. La tangente di un angolo è il
rapporto tra il cateto opposto all’angolo e quello adiacente
Calcolare il seno e il coseno di un angolo è un operazione che non si può fare a mente, i calcoli
sono semplici solo in alcuni casi particolari, per questa ragione si ricorre alle calcolatrici tascabili
oppure alle applicazioni di calcolo per personal computer o telefono, in passato si usavano delle
tavole.
I valori del seno e del coseno un angolo sono sempre compresi tra -1 e +1. Di seguito si riporta
una tabella riassuntiva dei valori per i principali angoli compresi tra 0° e 180°
ANGOLO
gradi
0°
30°
45°
60°
90°
120°
135°
150°
180°
α
radianti
0
π/6
π/4
π/3
π/2
2π/3
3π/4
5π/6
π
SEN(α)
esatto
0
1/2
√2/2
√3/2
1
√3/2
√2/2
1/2
0
SEN(α)
approssimato
0
0.5
0.707
0.866
1
0.866
0.707
0.5
0
COS(α)
esatto
1
√3/2
√2/2
1/2
0
-1/2
-√2/2
-√3/2
-1
COS(α)
TAN(α)
approssimato
1
0.866
0.707
0.5
0
-0.5
-0.707
-0.866
-1
TAN(α)
approssimato
0
√3/3
1
√3
non def.
−√3
-1
-√3/3
0
0
0.577
1
1.732
-1.732
-1
-0.577
0
(notiamo che la funzione SENO è crescente tra 0° e 90°, decrescente tra 90° e 180°, sempre positiva. La funzione
COSENO è sempre decrescente tra 0° e 180°, positiva tra 0° e 90°, negativa tra 90° e 180°. Vale per ogni angolo
l’identità goniometrica
+
= 1)
Nella tabella gli angoli sono espressi nei gradi sessagesimali (i normali gradi ai quali siamo abituati)
e in radianti, quest’ultimo modo di esprime gli angoli è diffuso in ambiente scientifico, in radianti
l’angolo piatto vale π (pi greco = 3.1459….). Le formule necessarie per fare la conversione da una
scala all’altra sono:
5
(angolo in gradi) = (angolo in radianti) ×
(angolo in radianti) = (angolo in gradi) ×
Per calcolare il valore delle funzioni SEN e COS (sulla calcolatrice sono SIN e COS) dobbiamo
verificare la modalità di espressione dell’angolo. Per usare i normali gradi è necessario che sul
display ci sia una scritta “DEG” o la semplice lettera “D”, per i radianti ci deve essere la scritta
“RAD” o la lettera “R”. C’è poi una terza modalità di esprimere gli angoli (angolo retto = 100) detta
“gradi centesimali”, in questo caso ci sarà la scritta “GRAD” o la lettera “G”. Per passare da una
modalità all’altra è necessario usare il tasto “DRG” (Deg – Rad – Grad).
L’utilizzo delle funzioni goniometriche in geometria permettere di “risolvere” un triangolo
rettangolo conoscendo un lato e un angolo (che non sia quello retto) piuttosto che due dei tre lati.
Sfruttando la definizione data all’inizio e potendo ricavare il valore delle funzioni SEN e COS con un
calcolatore o con le tabelle, è possibile determinare i cateti conoscendo l’ipotenusa:
a = c x SEN(α)
b = c x COS(α)
oppure l’ipotenusa conoscendo uno dei due cateti:
c = a / SEN(α)
c = b / COS(α)
L’utilità pratica delle funzioni goniometriche è legata al fatto che spesso è più semplice misurare
un anglo piuttosto che una distanza. Le misure degli
angoli si fanno con strumenti ottici
Come esempio di applicazione vediamo come sia
possibile misurare l’altezza di un edificio.
h
α
d
h
α1
d
α2
Si misura la distanza dalla base dell’edificio d e a
quella distanza si misura sotto quale angolo α è
visibile la l’altezza dell’edificio. L’ipotenusa c sarà c =
d/COS(α), mentre l’altezza h = c SEN(α)
Nel caso non sia possibile misurare la distanza dalla
base dell’oggetto di cui si intende misurare l’altezza h
si procederà in due fasi. Dopo una prima misura di
angolo α1, si avanzerà di un tratto d e si farà una
seconda misura di angolo α2. Per determinare l’altezza
h sono necessari i seguenti passaggi:
c1 = h/SEN(α1), c2 = h/SEN(α2). Osserviamo che la
distanza d è la differenza tra i cateti adiacenti agli
angoli α che si ottengono moltiplicando l’ipotenusa
6
per il coseno. d = c1COS(α1)-c2COS(α2). Sostituendo i valori di c1 e c2 si ha:
!
− , quindi per h avremo:
= "#$ % "#$ %
= $&' %
(
$&' %
Facciamo un esempio numerico:
Utilizzando i dati nella figura otteniamo:
= "#$ %
$&' %
α2 = 30°
!
"#$ %
(
$&' %
) .
= +.,-+
+./00
(
+..+.1++
=
) .
.23( .24
= 886
α = 20°
1
d = 90.0 m
Se il lettore ha riconosciuto la figura, sa anche che si
tratta di una misura più che realistica.
Le misure ottiche di angoli di elevazione posso essere fatte con semplicissimi strumenti (anche
fatti in casa) come quello descritto nella figura sottostante
Ecco come appare il grafico delle funzioni SENO e COSENO con gli angoli espressi rispettivamente
in gradi sessagesimali e radianti
7