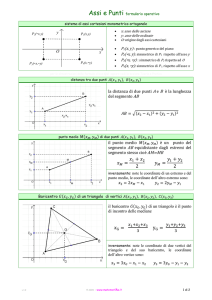
AREA DI UN TRIANGOLO NOTE LE COORDINATE DEI SUOI VERTICI
Dati tre punti di cui sono note le coordinate:
A ( x A ; y A ) , B ( xB ; yB ) e C ( xC ; yC ) , per determinare l’area del triangolo,
possiamo considerare AB come base, calcolare la distanza di C dalla base, ricavando così l’altezza
semiprodotto di base per altezza secondo la ben nota formula dell’area del triangolo:
1
AB ⋅ CH
2
AABC =
Esempio:
Siano A ( 2; 3 ) ,
CH e poi calcolare il
B ( 4;1 ) e C ( − 5; − 2 ) i vertici del triangolo ABC.
Calcolo innanzi tutto la lunghezza della base
AB =
AB :
( 4 − 2 ) 2 + (1 − 3 )2 = 2
2
Determino l’equazione della retta passante per i punti A e B, per poterne calcolare la distanza da C:
AB :
x − xA
y − yA
=
xB − x A
yB − y A
⇒
x−2 y−3
=
4 − 2 1−3
⇒
x−2 y−3
=
2
−2
⇒
x+ y−5=0
Calcolo la distanza di C dalla retta passante per i punti A e B, ottenendo l’altezza CH:
CH =
−5 − 2 − 5
A questo punto posso calcolare l’area del triangolo:
1 +1
2
2
AABC =
=
12
=6
2
2
1
1
AB ⋅ CH = ⋅ 2
2
2
2⋅6
2 = 12
Esiste un modo più semplice per calcolare l’area del triangolo, utilizzando il determinante di una matrice 2 x 2 così costruita:
AABC =
1 xC − x A
⋅
2 xB − x A
yC − y A
yB − y A
Dove il tutto è indicato in valore assoluto, in quanto l’area deve essere per forza positiva.
Per calcolare il determinante di una matrice 2 x 2 bisogna calcolare il prodotto dei termini della diagonale principale e sottrarre da
questa il prodotto dei termini della diagonale secondaria:
xC − x A
xB − x A
yC − y A
= ( xC − x A ) ( yB − y A ) − ( yC − y A ) ( xB − x A )
yB − y A
E ora possiamo rifare (più velocemente) l’esempio svolto prima:
AABC =
1 −5 − 2 − 2 − 3
1 −7 −5
⋅
=
⋅
4−2
1−3
2 −2
2
2
=
1
⋅ ( 14 + 10 ) = 12
2
Questo ci fornisce anche la condizione di allineamento di tre punti: l’area del triangolo è nulla se e solo se i tre vertici sono allineati.
In tal caso avremmo:
xC − xA
xB − x A
⇒
yC − y A
=0
yB − y A
⇒
( xC − x A ) ( yB − y A ) − ( yC − y A ) ( xB − x A ) = 0
( xC − x A ) ( yB − y A ) = ( yC − y A ) ( xB − x A )
Tre punti sono allineati se si verifica la seguente uguaglianza:
⇒
xC − x A
xB − x A
xC − xA
y − yA
= C
xB − x A
yB − y A
y − yA
= C
yB − y A
BIBLIOGRAFIA:
G. Zwirner, L. Scaglianti – L’essenza della matematica – Cedam vol. 1
ISBN 9788813208271