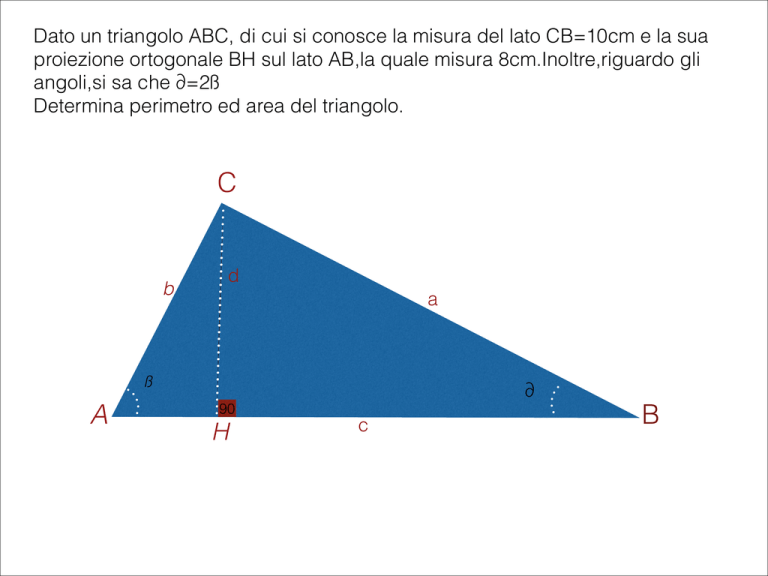
Dato un triangolo ABC, di cui si conosce la misura del lato CB=10cm e la sua
proiezione ortogonale BH sul lato AB,la quale misura 8cm.Inoltre,riguardo gli
angoli,si sa che ∂=2ß
Determina perimetro ed area del triangolo.
C
b
d
a
ß
A
∂
90
H
c
B
C
d
a
b
ß
A
∂
H
c
B
Con il primo teorema sui triangoli rettangoli:
!
BH
___
4
=__
cosß= CB
5
—————————————————————————————————————————
e per il teorema di Pitagora:
2
_
= 6cm
CH= BC — BH = 36cm
__
———————————————————————————————————————————
2
2
Conviene calcolare anche la tangente dell’angolo ß in funzione dei
cateti del triangolo BHC:
tanß= CH/BH=3
_
4
———————————————————————————
In tal modo è possibile determinare la tangente di ∂ :
!
2
tan∂=tan2ß=2tan(ß)/[1-tan(ß)]
———————————————————————————————————————————
Grazie a questo valore si può determinare la lunghezza del segmento AH:
!
. _7 = _7 cm
24 4
dunque:AB=
((8+7_4) cm=39cm
_
.
AH=HC cot∂=6cm
4
————————————————————————————————————————————
A questo punto intanto è possibile calcolare l’area del triangolo sia
con la classica formula che con il teorema dell’area:
!
2
S=117/4cm
—————————————————————————————————
Per calcolare il lato AC si osserva che è l’ipotenusa del triangolo
rettangolo AHC,dunque bisogna prima utilizzare la formula di
duplicazione del coseno per calcolare cosAlfa e poi la risoluzione dei
triangoli rettangoli.
!
Infine sommando i tre lati del triangolo ABC si trova che il perimetro é
2p=26cm
! —————————————————————————————————
Flavia Camilleri 4H












