Assi e Punti formulario operativo
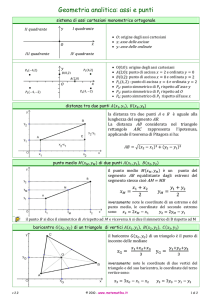
sistema di assi cartesiani monometrico ortogonale
P2(-x,y)
y
•
•
•
P1(x,y)
O
x
•
•
P4(x,-y)
P3(-x,-y)
•
•
x: asse delle ascisse
y: asse delle ordinate
O: origine degli assi cartesiani
P1(x, y) : punto generico del piano
P2(-x, y): simmetrico di P1 rispetto all’asse y
P3(-x, -y) : simmetrico di P1 rispetto ad O
P4(x, -y): simmetrico di P 1 rispetto all’asse x
per le dimostrazioni delle formule clicca qui oppure vedi la sezione Teoria e Pratica
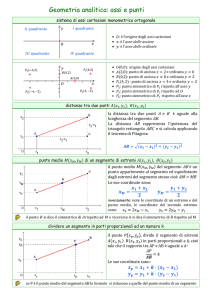
distanza tra due punti
la distanza di due punti A e B è la lunghezza
del segmento AB
punto medio
di due punti
il punto medio
è un punto del
segmento AB equidistante dagli estremi del
segmento stesso cioè AM=MB
inversamente: note le coordinate di un estremo e del
punto medio, le coordinate dell’altro estremo sono:
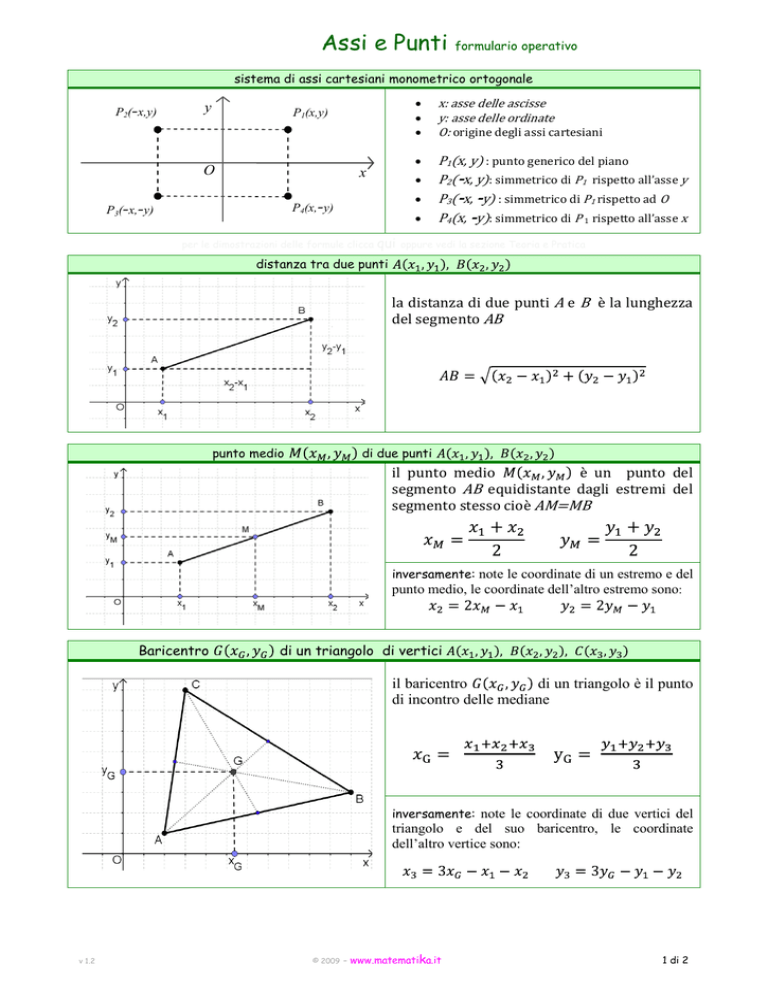
Baricentro
di un triangolo di vertici
il baricentro
di un triangolo è il punto
di incontro delle mediane
inversamente: note le coordinate di due vertici del
triangolo e del suo baricentro, le coordinate
dell’altro vertice sono:
v 1.2
© 2009
- www.matematika.it
1 di 2
Assi e Punti formulario operativo
ricerca dell’area di un triangolo di vertici
regola di Sarrus
l’area del triangolo di vertici
è uguale alla metà del valore assoluto del
determinante della matrice dei punti A, B, C
per calcolare il determinante è necessario:
metodo geometrico
C
F
yC
E
●
per calcolare l’area del triangolo ABC
•
yB
●
A
yA
•
B
D
●
xA
si calcola l’area del rettangolo ADEF circoscritto al
triangolo ABC
si sottraggono all’area del rettangolo, le aree dei tre
triangoli rettangoli ADB, BEC, CFA formati per
costruzione:
xB
xC
formule di geometria piana
C ●
a
b
●B
c
formula classica:
formula di Erone:
semiperimetro:
A ●
allineamento di tre punti
●
B
●
per verificare se tre punti A,B,C sono allineati si può:
•
C
●
•
●A
v 1.2
calcolare l’area del triangolo di vertici A,B,C
• se l’area è uguale a zero i punti sono allineati
oppure:
•
© 2009
calcolare le distanze AB, BC, AC
se AB+BC=AC i punti sono allineati
- www.matematika.it
2 di 2