Trasferimento di calore
Lezione II
Gaetano Festa
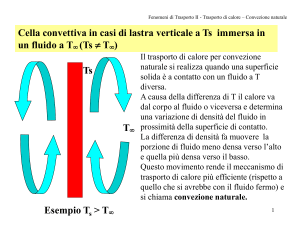
Convezione: ingredienti
Un fluido raffreddato dall’alto e/o riscaldato dal basso o dall’interno è
gravitazionalmente instabile perché le particelle in alto hanno densità
maggiore rispetto al resto.
freddo
celle convettive
caldo
Equazioni fondamentali
(1) Equazione del moto per sistemi continui
dv
ρ = f + ∇⋅σ
dt
moto delle particelle
Forza di gravità
(2) Equazione di continuità della massa
∂ρ
+ ρ∇⋅ v = 0
∂t
Nell’ipotesi di fluido incompressibile
ρ = cost ⇒ ∇⋅ v = 0
Tensore degli sforzi
Equazioni fondamentali
(3) Relazione costitutiva
In un fluido ideale il tensore degli sforzi è isotropo (legge di Stevino)
σ = − p1
p è la pressione.
Il mantello è un fluido viscoso
σ = f (ρ , ∇vS ) f ( ρ , D)
1 ∂vi ∂v j
Dij =
+
2 ∂x j ∂xi
Per variazioni infinitesime la relazione costitutiva si riduce a quella di un
fluido newtoniano
σ = − p1 + 2µD
viscosità
Equazioni fondamentali
(4) Approssimazione di Boussinesq
Le variazioni di gravità possono essere considerate trascurabili per cui il
fluido può considerarsi incompressibile, eccetto che nella forza di gravità,
dove le variazioni determinano il disequilibrio con la pressione idrostatica
Fluido incompressibile
∂ρ
= 0; ∇ρ = 0
∂t
Equilibrio idrostatico
ρ0g = −∇p
Per il contributo di
gravità
ρ = ρ0 + ρ '
Equazioni fondamentali
(5) Equazione del calore
dT
ρc = ∇⋅ (k∇T ) + A
dt
∂T
1
A
+ v ⋅∇T = ∇⋅ (k∇T ) +
∂t
ρc
ρc
Equazioni fondamentali
Combinando insieme l’equazione del momento e quella costitutiva si ha
dv
ρ = ρg + ∇⋅ ( − p1 + 2µD)
dt
Per componenti
∂
ρvi = ρ gi +
∂x j
∂vi ∂v j
+
− pδij + µ
∂x j ∂xi
∂p
∂
2
ρvi = ρ gi − + µ∇ vi + µ ∇⋅ v
∂xi
∂xi
fluido incompressibile
ρ v = ρg −∇p + µ∇2 v
∇⋅ v = 0
Eq. di Navier-Stokes
Condizioni stazionarie
In condizioni stazionarie la derivata della velocità euleriana rispetto al
tempo è nulla.
ρg −∇p + µ∇2 v = 0
In 2D, per componenti (mezzo cartesiano)
∂p
+ µ∇2vx = 0
∂x
∂p
− + ρ0 g + ρ ' g + µ∇2vz = 0
∂z
−
Consideriamo la pressione relativa come
P = p − ρ0 gz
Equazioni finali
∂P
− + µ∇2vx = 0
∂x
∂P
− + ρ ' g + µ∇2vz = 0
∂z
Le variazioni di densità al prim’ordine sono legate a variazioni di temperatura
e sono locali (l’effetto di variazioni di temperatura in un punto non
influenzano la densità in punti distanti).
Per la dilatazione volumetrica
dV = αVdT
Poiché la massa si conserva
0 = dm = d (ρV ) = Vd ρ + ρ dV ⇒
dV
dρ
=−
ρ
V
d ρ = −αρdT
Integrando alle differenze finite
ρ ' = ρ − ρ0 = −αρ0 (T − T0 )
Condizioni per la convezione
Si consideri un liquido a
temperatura T0 riscaldato dal
basso a temperatura T1 > T0. Nella
parte più bassa dT >0 , dρ < 0.
Le particelle di liquido sono più
leggere e trovandosi in basso
diventano gravitazionalmente
instabili.
(Forze gravitazionali)
> (Forze viscose)
Convezione
Da conduzione alla convezione
Supponiamo di partire dalla
condizione T1 = T0 e poi di far
crescere T1 lentamente.
Inizialmente la gravità non è in
grado di vincere la viscosità e non
c’è moto
b
z
Fluido stazionario
v = 0;
∂T
=0
∂t
Il calore si propaga per conduzione
In un mezzo 1D
Tc ( z) =
∂2Tc
=0
2
∂z
T1 + T0 T1 − T0
+
z
2
b
∇2Tc = 0
La temperatura varia linearmente
Analisi di stabilità lineare
b
z
Supponiamo di aumentare la
differenza T1 - T0 fino al limite
oltre al quale inizia la convezione.
Aggiungiamo una perturbazione
in temperatura, per la quale inizia
la convezione.
La variazione di temperatura rispetto al modello conduttivo limite
T1 + T0 T1 − T0
T '( x, z) = T ( x, z) − Tc ( z) = T ( x, z) −
−
z
2
b
Rimpiazzando T’ con T nell’equazione del calore si ha
∂T ∂T '
=
; ∇2T = ∇2T ';
∂t
∂t
T1 − T0
v ⋅∇T = v ⋅∇T '+ vz
;
b
T1 + T0 T1 − T0
T = T '+
+
z;
2
b
Equazioni
Equazione del calore risultante
T −T
∂T '
+ v ⋅∇T '+ vz 1 0 = κ∇ 2T '
∂t
b
termine del second’ordine; v piccolo (limite inferiore della convezione);
Incompressibilità
Momento
Calore
∂vx ∂vz
+
=0
∂x ∂z
∂p
− + µ∇2vx = 0
∂x
∂p
− + ρ0 g + ρ ' g + µ∇2vz = 0
∂z
T1 − T0
∂T '
+ vz
= κ∇ 2T '
∂t
b
Condizioni al contorno
Poiché la temperatura è fissata
agli estremi
b
T ( z = −b / 2) = T0
T ( z = b / 2) = T1
z
T '( z = ±b / 2) = 0
Negli estremi vale anche: vz = 0
C’è bisogno di una ulteriore condizione
Bordo rigido
Bordo libero
vx = 0
∂vx ∂vz ∂vx
σ xz = 0;
+
=
=0
∂z ∂x ∂z
Funzione stream
v = ∇×ψ
∇⋅ v = 0
v = (vx ,0, vz )
ψ = (0,ψ ,0)
∂ψ
vx = −
∂z
∂ψ
vz =
∂x
E’possibile scrivere le equazioni del momento e della temperatura in
funzione dello stream anziché della velocità
La soluzione generale è
T ' = T cos(π z / b)cos(kx x) f (t )
ψ = ψ cos(π z / b)sin(kx x) f (t )
T '( z = ±b / 2) = 0
∂ψ
=0
vz ( z = ±b / 2) =
∂x
∂vx
∂2ψ
( z = ±b / 2) = 2 = 0
∂z
∂z
Dipendenza temporale
Cosa possiamo dire sulla funzione f(t) ? Dall’equazione del calore si ha
∂T ' ∂ψ T1 − T0
+
= κ∇ 2T '
∂t
∂x b
T1 − T0
T cos(π z / b) cos(k x x) f '(t ) + ψ k x cos(π z / b) cos(k x x) f (t )
+
b
π2
2
κ T 2 + k x cos(π z / b) cos(k x x) f (t ) = 0
b
π2
T1 − T0
2
Tf '(t ) +ψ k x
f (t ) + κ T 2 + k x f (t ) = 0
b
b
ψ T1 − T0
π2
f '(t )
2
= − kx
+ κ 2 + kx = α
f (t )
b
b
T
Dipendenza temporale
f '(t )
=α
f (t )
α >0 ⇒
f (t ) = e
αt
α <0 ⇒
f (t ) = e
−α t
Instabile : la convezione aumenta
Stabile: la convezione cessa
Equazione del calore
T1 − T0
π2
2
ψ kx
+ κT α + 2 + kx = 0
b
b
(1) Anche l’equazione del momento presenta un’equazione omogenea
(2) Soluzioni non banali per determinante nullo
ψ
(3) Dall’equazione del momento possiamo ricavare il rapporto
T
Numero di Rayleigh
κ ρ 0 gα v (T1 − T0 )b3 2 2
2
2 2
k b − (π + (k x b ))
α= 2
2
2 2 2 x
b µκ (π + (k x b ))
ρ0 gα v (T1 − T0 )b3
Ra =
µκ
Ra k x2b 2 − (π 2 + (k x2b 2 ))3
α=
(π 2 + (k x2b 2 )) 2
κ
b2
Domini di stabilità
La convezione ha luogo se
2 2
x
2
2
2
2 2
x
2
3
Ra k b − (π + (k b ))
α=
>0
2 2
κ
(π + (k x b ))
b
(π 2 + (k x2b 2 ))3
Racrit (k x b) =
k x2b 2
(π 2 + (k x2b 2 ))3
Ra >
k x2b 2
Instabile
2
3
(
π
+
q
)
Minimo
q
Stabile
3q(π 2 + q) 2 − (π 2 + q )3 = 0
2
2q − π = 0
q=
π2
2
kxb =
π
2
; Racrit = 657
Mantello terrestre
Se T1-T0 cresce da zero, la condizione
critica impone che il rapporto tra le
dimensioni orizzontale e verticale sia 2
Condizioni di zero slip all’interfaccia le
soluzioni numeriche indicano che
Racrit=1700
Se il mezzo è raffreddato dall’alto e
riscaldato dall’interno, con rate H
RaH
α v ρ 02 gH b 5
=
k µκ
Zero slip : Racrit=2772; kxb=2.63
Free boundary : Racrit=868, kxb=1.79
b = 700km(UM ) ⇒ Ra = 2 106
b = 2900km( AM ) ⇒ Ra = 109
µ = 1021 Pa s
K = 4W / (mK );κ = 10−6 m2 / s
αv = 3 10−5 K −1 ; g = 10m / s 2
ρ = 4 g / cm3 ; H = 91012 W / kg
Ampiezza della convezione
L’analisi di stabilità definisce soltanto le condizioni per la convezione, ma non le
caratteristiche in termini di temperatura e moto (soluzione non lineare)
Una soluzione completa è possibile solo numericamente, possiamo fare delle ipotesi
nel caso in cui la condizione è vigorosa (Ra>> Racrit )
In tal caso il fluido si mescola così rapidamente da considerare il fluido isotermo alla
temperatura
T1 + T0
2
con un salto di temperatura alle interfacce superiore e inferiore.
Tale condizione non è stabile, ma genera dei strati limite nei quali si verifica il
gradiente termico
Per la definizione dello strato si utilizza un approccio lineare di stabilità
Geoterme nel mantello
• Alla base della litosfera oceanica la temperatura è dell’ordine di 1600 °K (strato
limite superiore)
• All’interno del mantello la temperatura aumenta, a causa dell’aumento della
pressione esercitata dalla parte sovrastante.
• Si può assumere che tutto il lavoro esercitato per la compressione della roccia
la riscalda senza che vi sia scambio di calore con le rocce circostanti. La
temperatura aumenta lungo un’adiabatica.
• Dal secondo principio della termodinamica la variazione dell’entropia per
unità di massa è
αv
dq c p
ds = = dT − dp
T T
ρ
• Lungo un’adiabatica reversibile : ds=0
dT αvT
=
dp S ρcp
Geoterme nel mantello
• Se la rocce è incompressibile non c’è gradiente adiabatico.
dT dT dz
1 dT
=
=
dp
dz
dp
ρ
g
dz S
S
S
• Il gradiente adiabatico è dunque
dT αv gT
=
cP
dz S
• Alla base della litosfera oceanica
αv = 3 10−5 K −1 ;
g = 10m / s 2
T = 1600K
cP = 103 J / ( K kg )
dT
= 0.5K / km
dz
Geoterme nel mantello
dT
= 0.3K / km
dz
• Nel mantello superiore al di sotto della litosfera
• Discontinuità strutturali : 410 km (olivina -> spinello), 660 km (spinello ->
perovskite e magnetowustite).
L
∆T =
cP
410 km
esotermica
660 km
endotermica
L = 90 KJ / kg ; c p = 1 KJ / (kg K )
L = −70 KJ / kg; c p = 1 KJ / (kg K )
∆T = 90K
∆T = −70 K
• (a) la convezione interessa tutto il mantello o
• (b) ci sono due celle convettive. La discontinuità 660 km è
uno strato termico limite.
• (c) Ci sono delle condizioni miste
Fine
Caratteristiche dello strato
Flusso di calore
Numero di Nusselt
La profondità massima dei terremoti nelle zone di subduzione è 660 km.
Possiamo assumere che la convezione interessi la parte superiore del mantello
b = 700km
T1 − T0 = 1500K
ρ0 = 3700kg / m3 κ = 10−6 m2 / s
g = 10m / s 2
−5
α v = 3 10 K
µ = 1021 Pa s
−1
k = 4W / ( m K )
Ra = 5.7 105
q = 85 mW / m2
tc = 50Myr
Mantello Terrestre
Soluzioni stazionarie in un fluido raffreddato dall’alto (litosfera oceanica)
e riscaldato dall’interno (produzione di calore radiogenica).
Modelli a celle di dimensione verticale b e orizzontale λ/2.
Ai bordi delle celle convettive (in principio
soltanto ad uno) si creano condotti (plume) di
materiale freddo discendente (litosfera
oceanica in subduzione), al centro il materiale è
isotermico
Osservabili : flusso di calore in superficie,
velocità delle placche.
Forze in gioco nella tettonica : forza gravitazionale, legata al gradiente termico tra la
litosfera ed il mantello circostante, ridge push, dovuta alle spinte laterali del ridge,
trench pull, dovuta alla risalita della transizione olivina-spinello
Funzione stream
Soluzioni per separazione
Transizione olivina -spinello
Curva di Clapeyron: pressione /temperatura per la transizione di fase
Alla stessa profondità c’è un gradiente termico,dovuto alla
litosfera che sprofonda, quindi le stesse condizioni si
cambiamento di fase si ottengono a pressioni inferiori e
dunque a quote inferiori.
La variazione di quota è dell’ordine di 40 km, la forza associata è ca la metà di quella
gravitazionale