Nessun titolo diapositiva

Fenomeni di Trasporto II - Trasporto di calore – Convezione naturale
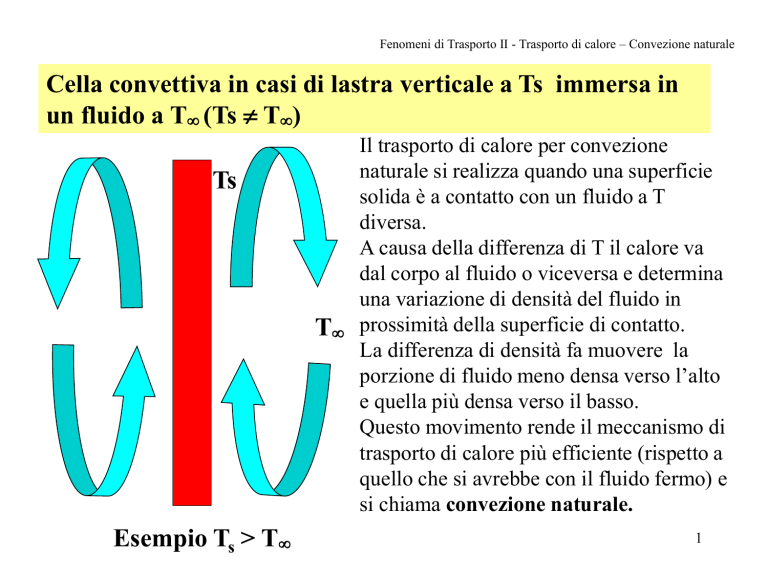
Cella convettiva in casi di lastra verticale a Ts immersa in
un fluido a T (Ts  T)
Ts
T
Esempio Ts > T
Il trasporto di calore per convezione
naturale si realizza quando una superficie
solida è a contatto con un fluido a T
diversa.
A causa della differenza di T il calore va
dal corpo al fluido o viceversa e determina
una variazione di densità del fluido in
prossimità della superficie di contatto.
La differenza di densità fa muovere la
porzione di fluido meno densa verso l’alto
e quella più densa verso il basso.
Questo movimento rende il meccanismo di
trasporto di calore più efficiente (rispetto a
quello che si avrebbe con il fluido fermo) e
si chiama convezione naturale.
1
Fenomeni di Trasporto II - Trasporto di calore – Convezione naturale
Convezione naturale Ipotesi e definizione di Nu
Ipotesi
1) superficie solida a temperatura uniforme Ts
2) fluido a temperatura uniforme T
3) condizioni stazionarie
Si definisce un numero di Nusselt medio che ha la stessa
definizione di quello visto in caso di convezione forzata
hL
Nu 
kf
NON E’ POSSIBILE DEFINIRE UN NUMERO DI Re
PERCHE’ NON C’E’ UNA V CARATTERISTICA NOTA
2
Fenomeni di Trasporto II - Trasporto di calore – Convezione naturale
Coefficiente di espansione termica
Nei fluidi sia gas che liquidi una variazione della T nello spazio
determina variazioni della densità
1   
      = coefficiente di espansione termica [1/K]
  T  P
densità espressa mediante

 (T )   
T  T  ... espansione in serie di Taylor
T T
T  T di riferimento


Trattandosi di piccole variazioni di T e di densità la
serie di Taylor si ferma al primo termine

 (T )      T  T

    T
3
Fenomeni di Trasporto II - Trasporto di calore – Convezione naturale
Numero di Grashof
T
z
z
   T   T
0
1
0
T1
T
L
F  g  A L
1
T2
x
ub ub A
= forza che determina
il moto

Incremento della qdm atteso a seguito della
applicazione della forza F (portata di qdm)
1/ 2
2
g  A L   ub A
 gL  

ub  




4
Fenomeni di Trasporto II - Trasporto di calore – Convezione naturale
Numero di Grashof
 ub L
Re b 

Numero di Reynolds
1/ 2
3  

 ub L   gL

Re b 

 2  



2

forze di galleggiamento
forze viscose
2
2 3
3 
 gL
 gL
3
Gr 

 T   L T
2
2


2

 g

2

T  Ts  T
I valori di  sono tabellati
(Kreith) dipendono solo dal
fluido, T e P
5
Fenomeni di Trasporto II - Trasporto di calore – Convezione naturale
Numero di Grashof
In caso di trasporto per convenzione forzata era Nu = f (Re, Pr)
In caso di trasporto per convezione naturale è
Nu = f ( Gr,Pr)
Gr = numero di Grashof
 g  L Ts  T
Gr 
2

2
3
Forze di galleggiamento
Forze viscose
g = accelerazione di gravità = 9.8 [m s-2]
 = coefficiente di espansione termica [K-1]
L = lunghezza caratteristica [m]
Le proprietà del fluido (  ) vanno
valutate alla temperatura di film
T f  ( Ts  T ) / 2
6
Fenomeni di Trasporto II - Trasporto di calore-Convezione naturale
Numero di Grashof per gas ideali
Per un gas ideale (T>>Tc) per il quale vale la legge di stato
PV = nRT essendo:
 = -1/ (  / T)p
risulta
 = (1/Tf)
Quindi il numero di Grashof per gas ideali risulta:
 2 g L3 ( Ts  T )
Gr 
Tf
2
7
Fenomeni di Trasporto II - Trasporto di calore – Convezione naturale
Convezione naturale: correlazioni per il calcolo del
coefficiente di trasporto di calore
Le correlazioni sono in genere espresse nella forma:
Nu  a Gr Pr   a Ra 
m
m
Ra = numero di Rayleigh
1) le proprietà fisiche sono valutate a T film
2) occorre scegliere correttamente L
3) le correlazioni sono in genere valide per un intervallo di
valori di Gr, Pr o Ra
8
Fenomeni di Trasporto II - Trasporto di calore – Convezione naturale
Convezione naturale: espressioni di Nu per diverse geometrie
Nu  a Gr Pr 
m
(Eq. 5-32 Perry Tab. 14.4.1 Middleman)
Geometria
Parete piana verticale LH< 3 ft
Cilindro orizzontale L  D < 8in
Y =Gr  Pr
a
m
< 104
1.36
1/5
104 <Y< 109
0.59
1/4
> 109
0.13
1/3
< 10-5
0.49
0
10-5 <Y< 10-3
0.71
1/25
10-3 <Y< 1
1.09
1/10
1 < Y< 104
1.09
1/5
104 < Y< 109
0.53
1/4
> 109
0.13
1/3
9
Fenomeni di Trasporto II - Trasporto di calore – Convezione naturale
Convezione naturale: altre espressioni di Nu
Sfera (L caratteristica = D)
103 < Gr < 109
Pr > 0.5
Nu D  2  0.45( GrD Pr)1 / 4
1/ 6
1/ 2
L
Nu
 Nu
1/ 2
0


Ra
/
300
L


 1  0.5 / Pr 9 /16 16 / 9 




Eq. Churchill e Chu
Geometria
L
Nuo
Sup verticale
L
0.68
Cilindro verticale
L
0.68
Cilindro orizzontale
D
0.36 
Sfera
D/2

10