Equazioni goniometriche elementari
annuncio pubblicitario
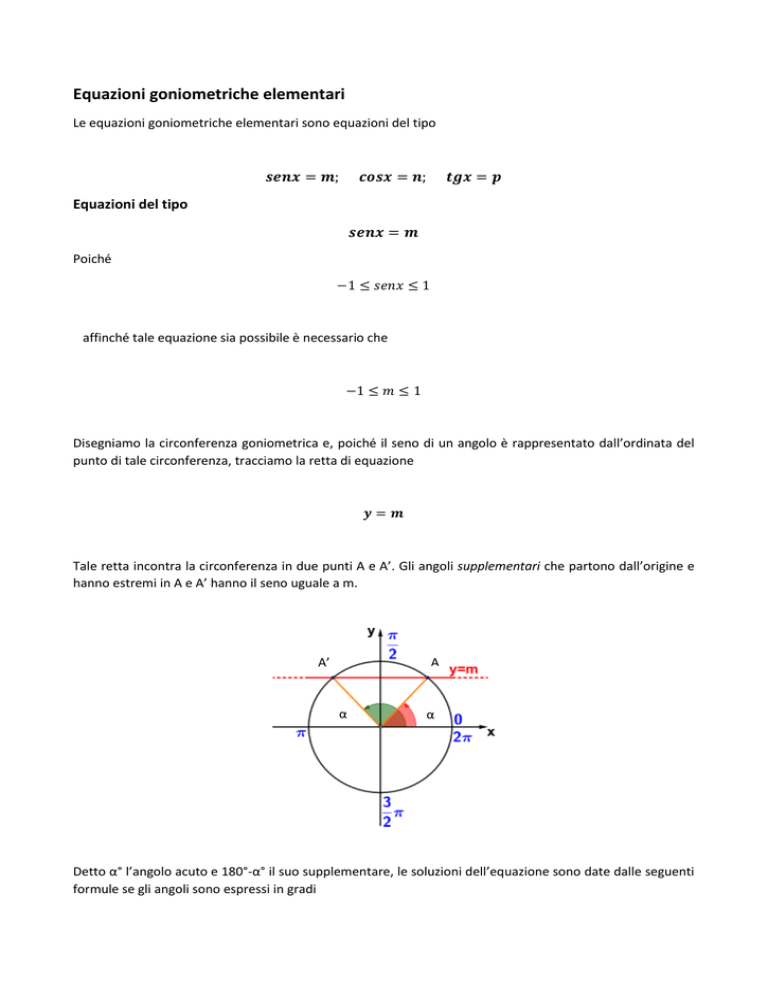
Equazioni goniometriche elementari Le equazioni goniometriche elementari sono equazioni del tipo ππππ = π; ππππ = π; πππ = π Equazioni del tipo ππππ = π Poiché −1 ≤ π πππ₯ ≤ 1 affinché tale equazione sia possibile è necessario che −1 ≤ π ≤ 1 Disegniamo la circonferenza goniometrica e, poiché il seno di un angolo è rappresentato dall’ordinata del punto di tale circonferenza, tracciamo la retta di equazione π=π Tale retta incontra la circonferenza in due punti A e A’. Gli angoli supplementari che partono dall’origine e hanno estremi in A e A’ hanno il seno uguale a m. A’ A α α Detto α° l’angolo acuto e 180°-α° il suo supplementare, le soluzioni dell’equazione sono date dalle seguenti formule se gli angoli sono espressi in gradi π = πΆ° + ππππ° ∨ π = πππ° − πΆ° + ππππ° πππ π ∈ π E dalle seguenti formule se gli angoli sono espressi in radianti π = πΆπ + πππ ∨ π = π − πΆπ + πππ πππ π ∈ π Esempio 1 π πππ₯ = 1 2 Facciamo la rappresentazione grafica Le soluzioni dell’equazione sono date dalle formule π₯= π + 2ππ 6 ∨ π₯=π− Esempio 2 π πππ₯ = 3 Poiché 2 > 1 l’equazione non ha soluzioni. 3 2 π + 2ππ 6 Esempio 3 π πππ₯ = − √3 2 Le soluzioni dell’equazione sono date dalle formule π₯ =π+ π + 2ππ 3 ∨ π π₯ = − + 2ππ 3 Esempio 3 π πππ₯ = − 2 3 Facciamo la rappresentazione grafica y=-2/3 L’equazione è soddisfatta dalle formule 2 π₯ = ππππ ππ (− ) + 2ππ 3 ∨ 2 π₯ = [π − ππππ ππ (− )] + 2ππ 3 Equazioni del tipo ππππ = π Poiché −1 ≤ πππ π₯ ≤ 1 affinché tale equazione sia possibile è necessario che −1 ≤ π ≤ 1 Disegniamo la circonferenza goniometrica e, poiché il coseno di un angolo è rappresentato dall’ascissa del punto di tale circonferenza, tracciamo la retta di equazione π=π Tale retta incontra la circonferenza in due punti P e P’. Tenendo presente che la funzione coseno è pari, gli angoli opposti che partono dall’origine A e hanno estremi in P e P’ hanno il coseno uguale a n. Le soluzioni dell’equazione sono date dalle seguenti formule se gli angoli sono espressi in gradi π = πΆ° + ππππ° ∨ π = −πΆ° + ππππ° πππ π ∈ π E dalle seguenti formule se gli angoli sono espressi in radianti π = πΆπ + πππ ∨ π = −πΆπ + πππ πππ π ∈ π Esempio 1 πππ π₯ = − √3 2 Facciamo la rappresentazione grafica 150° -150° Le soluzioni dell’equazione sono π₯ = 150° + π360° ∨ π₯ = −150 + π360° Esempio 2 πππ π₯ = 1 2 Facciamo la rappresentazione grafica π/3 -π/3 Le soluzioni dell’equazione sono π₯= π + 2ππ 3 ∨ π₯=− π + 2ππ 3 Esempio 3 π 1 cos (2π₯ − ) = − 6 2 Facciamo la rappresentazione grafica Le soluzioni dell’equazione si ottengono risolvendo le due equazioni π 2π = + 2ππ 6 3 ∨ 2π₯ − 12π₯ − π = 4π + 12ππ ∨ 12π₯ − π = −4π + 12ππ 12π₯ = 5π + 12ππ ∨ 12π₯ = −3π + 12ππ 5 π + ππ 12 ∨ 1 π₯ = − π + ππ 4 2π₯ − π₯= π 2π =− + 2ππ 6 3 Equazioni del tipo πππ = π Sulla tangente geometrica condotta per il punto A prendiamo il punto T di ordinata p; la retta OT incontra la circonferenza in due punti diametralmente opposti che sono gli estremi di tutti gli archi che hanno tangente uguale a p. p Detta α° l’ampiezza dell’arco positivo che termina in P e ricordando che la tangente è periodica di periodo 180°, le soluzioni dell’equazione sono date dalla formula π = πΆ + ππππ° E in radianti da π = πΆ + ππ Esempio 1 π‘ππ₯ = − Facciamo la rappresentazione grafica 3 2 Le soluzioni dell’equazione si ottengono dalla seguente formula 3 π₯ = ππππ‘π (− ) + ππ 2 Esempio 2 Risolvere la seguente equazione con la condizione 0 ≤ π₯ < 360° π‘π(180° + 3π₯) = 1 Facciamo la rappresentazione grafica Le soluzioni dell’equazione si ottengono dalla seguente formula 180° + 3π₯ = 45° + π180° 3π₯ = 45° + π180° π₯ = 15° + π60° Le soluzioni si ottengono sostituendo a k = 0; 1; 2…. Fino a che si ottengono angoli soddisfacenti la condizione 0 ≤ π₯ < 360° Le soluzioni sono ππ°; ππ°; πππ°; πππ°; πππ°; πππ° Particolari equazioni goniometriche elementari π³′ πππππππππ ππππΆ = ππππ· Tenendo conto della periodicità della funzione seno, due angoli di circonferenza hanno lo stesso seno se tali angoli sono uguali o supplementari, cioè πΆ = π· + πππ ∨ πΆ = π − π· + πππ Esempio 1 π ππ(3π₯ − 30°) = π ππ(10° − π₯) In base alle precedenti formule possiamo scrivere 3π₯ − 30° = 10° − π₯ + π360° ∨ 3π₯ − 30° = 180° − 10° + π₯ + π360° E risolvendo otteniamo 4π₯° = 40° + π360° ∨ 2π₯ = 200° + π360° π₯° = 10° + π90° ∨ π₯ = 100° + π180° Esempio 2 π ππ(20° + 2π₯) + π ππ(π₯ − 40°) = 0 π ππ(20° + 2π₯) = −π ππ(π₯ − 40°) Poiché la funzione seno è dispari, cioè π ππ(−π₯) = −π πππ₯, possiamo scrivere π ππ(20° + 2π₯) = π ππ(−π₯ + 40°) Ci siamo ricondotti al caso precedente e quindi 20° + 2π₯ = −π₯ + 40° + π360° ∨ 20° + 2π₯ = 180° + π₯ − 40° + π360° Risolvendo otteniamo 3π₯ = 20° + π360° ∨ π₯ = 120° + π360° π₯ = 6°40′ + π120° ∨ π₯ = 120° + π360° Esempio 3 π ππ3π₯ = πππ (π₯ − 30°) Per le proprietà degli archi associati, sappiamo che πππ πΌ = π ππ(90° − πΌ) quindi π ππ3π₯ = π ππ(90 − π₯ + 30°) 3π₯ = 120° − π₯ + π360° ∨ 4π₯ = 120° + π360° π₯ = 30° + π90° 3π₯ = 180° − 120° + π₯ + π360° ∨ ∨ 2π₯ = 60° + π360° π₯ = 30° + π180° La soluzione π₯ = 30° + π90° Include anche la soluzione π₯ = 30° + π180° Per cui come soluzione finale possiamo scrivere π₯ = 30° + π90° Esempio 4 π ππ(20° − π₯) = −πππ (2π₯ − 10°) Dagli archi non associati sappiamo che πππ πΌ = π ππ(90° − πΌ) → −πππ πΌ = −π ππ(90° − πΌ) → −πππ πΌ = π ππ(−90° + πΌ) L’equazione può, quindi, essere scritta come π ππ(20° − π₯) = π ππ(−90° + 2π₯ − 10°) π ππ(20° − π₯) = π ππ(−100° + 2π₯) 20° − π₯ = −100° + 2π₯ + π360° ∨ −3π₯ = −120° + π360° 20° − π₯ = 180° + 100° − 2π₯ + π360° ∨ 3π₯ = 120° + π360° π₯ = 40° + π120° ∨ ∨ π₯ = 260° − 2π₯ + π360° π₯ = 260° + π360° π₯ = 260° + π360° π³′ πππππππππ ππππΆ = ππππ· Tenendo conto della parità e della periodicità della funzione coseno, due angoli di circonferenza hanno lo stesso coseno se sono opposti, cioè πΆ = π· + πππ ∨ πΆ = −π· + πππ Esempio 1 3 π πππ ( π − 4π₯) = πππ (2π₯ − ) 4 3 In base alle precedenti formule possiamo scrivere 3 π π − 4π₯ = 2π₯ − + 2ππ 4 3 3 π π − 4π₯ = −2π₯ + + 2ππ 4 3 ∨ E risolvendo otteniamo 9π − 48π₯ = 24π₯ − 4π + 24ππ ∨ 9π − 48π₯ = −24π₯ + 4π + 24ππ 72π₯ = 13π + 24ππ ∨ 24π₯ = 5π + 24ππ 13 π π+π 72 3 ∨ π₯= π₯= 5 π + ππ 24 Esempio 2 πππ (50° + π₯) = −πππ (20° − 2π₯) In base alle precedenti formule e tendo presente che –cosα = cos(π-α) possiamo scrivere πππ (50° + π₯) = πππ (180° − 20° + 2π₯) πππ (50° + π₯) = πππ (160° + 2π₯) 50° + π₯ = 160° + 2π₯ + π360° ∨ 50° + π₯ = −160° − 2π₯ + π360° ∨ 3π₯ = −210° + π360° E risolvendo otteniamo π₯ = −110° + π360° π₯ = −110° + π360° ∨ π₯ = −70° + π120° π³′ πππππππππ πππΆ = πππ· Tenendo presente la periodicità della funzione tangente, due angoli di circonferenza hanno la stessa tangente se tali angoli differiscono per un numero intero di semicirconferenze, cioè πΆ = π· + ππ Esempio 1 π π π‘π (3π₯ + ) = π‘π(4π₯ − ) 7 8 In base alla precedente formula possiamo scrivere 3π₯ + π π = 4π₯ − + ππ 7 8 E risolvendo otteniamo π₯= π π + − ππ 7 8 π₯= 15 π − ππ 56 Esempio 2 π‘π(3π₯ + 65°) = −π‘π(2π₯ − 25°) Poiché la funzione tangente è dispari e cioè -tgx = tg(-x), possiamo scrivere π‘π(3π₯ + 65°) = π‘π(−2π₯ + 25°) 3π₯ + 65° = −2π₯ + 25° + π180° 5π₯ = −40° + π180° π₯ = −8° + π36° Esempio 3 π‘π(2π₯ − 30°) = ππ‘π(π₯ − 30°) Poiché ππ‘ππ₯ = π‘π(90° − π₯) possiamo scrivere π‘π(2π₯ − 30°) = π‘π(90° − π₯ + 30°) π‘π(2π₯ − 30°) = π‘π(120° − π₯) 2π₯ − 30° = 120° − π₯ + π180° 3π₯ = 150° + π180° π₯ = 50° + π60° Esempio 4 π‘π(2π₯ + 30°) = −ππ‘π(π₯ + 45°) Poiché la funzione cotangente è dispari −ππ‘ππ₯ = ππ‘π(−π₯) possiamo scrivere π‘π(2π₯ + 30°) = ππ‘π(−π₯ − 45°) π‘π(2π₯ + 30°) = π‘π(90 + π₯ + 45°) π‘π(2π₯ + 30°) = π‘π(135° + π₯) 2π₯ + 30° = 135° + π₯ + π180° π₯ = 105° + π180° Bibliografia N. Dodero – P. Baroncini – R. Manfredi: Elementi di matematica 3 – Ghisetti & Corvi editori M. Bergamini – A. Trifone – G. Barozzi: Matematica.blu.2.0 - Zanichelli
