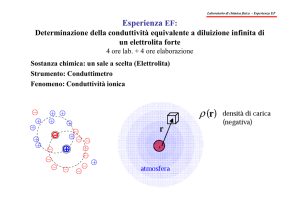
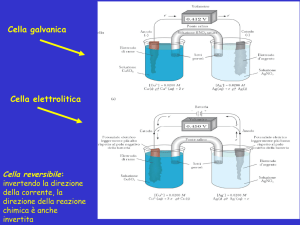
CONDUTTANZA ELETTRICA DI UN ELETTROLITA IN SOLUZIONE
(TEORIA)
Se si applica una differenza di potenziale elettrico fra due elettrodi immersi in una soluzione
ionica, si verifica una migrazione risultante di ioni in direzione dell’uno o dell’altro elettrodo e la
soluzione viene attraversata da una corrente elettrica. L’entità di tale corrente è strettamente legata
alla conduttanza elettrica della soluzione ionica, denominata anche conducibilità elettrica,
ovvero all’attitudine di un elettrolita a trasportare una corrente elettrica.
Dato che la conduttanza è strettamente correlata con la concentrazione degli ioni in soluzione, la
misura sperimentale della conducibilità elettrica è un metodo ampiamente usato per determinare la
concentrazione di una data specie ionica e quindi per calcolare delle costanti di equilibrio oppure
per studiare la cinetica di una reazione chimica, in cui partecipano degli ioni.
L’entità di corrente che passa in una soluzione elettrolitica è definita dalla legge di Ohm in maniera
analoga a quanto fatto per i conduttori metallici ovvero
V I R
dove
V è la differenza di potenziale applicata ai capi degli elettrodi espressa in Volt
R è la resistenza elettrica della soluzione espressa in ohm
I è la corrente espressa in Ampere
In base alla seconda legge di Ohm la resistenza R di un conduttore metallico e quindi anche di una
soluzione elettrolitica ,dipende dalla sua geometria ovvero dalla lunghezza l e dalla sezione S:
R
l
S
dove viene denominata resistività specifica della soluzione, ovvero è la resistenza di una celletta
contenente un elettrolita di lunghezza e sezione unitarie . Se l=1cm e S=1cm 2 , allora si riferisce
alla resistività specifica di un volume di forma cubica pari a 1 cm3 di soluzione elettrolitica.
La conduttanza L viene definita come l’inverso della resistenza ovvero
L
1
R
ed è espressa in Siemens (S = ohm-1).
Pertanto da misure di resistenza di una soluzione ionica è possibile risalire alla conduttanza elettrica
della soluzione.
Tuttavia, dato che quest’ultima dipende dalla geometria della cella utilizzata per eseguire le misure,
ovvero dal volume della soluzione elettrolitica, di solito si considera, al suo posto, la conduttanza
specifica (o conducibilità specifica), che fa riferimento a un volume di soluzione pari a 1 cm3 e
che è definita come il reciproco della resistività specifica ovvero
1 l
R S
dove l= 1cm e S=1cm2 e l’unità di misura di è Siemens x cm-1.
Pertanto, per determinare sperimentalmente la conduttanza specifica di un elettrolita, si fa passare
una corrente elettrica in una cella conduttometrica la cui geometria è tale da contenere 1 cm 3 di
soluzione. In laboratorio di solito si utilizzano delle cellette di vetro che sostengono due lamine di
platino che, idealmente, hanno la sezione pari a 1 cm2, sono poste alla distanza di 1 cm e
contengono teoricamente un volume di forma cubica pari a 1 cm3. Queste cellette vengono immerse
nella soluzione di cui si vuole misurare la conduttanza specifica. Esistono comunque delle cellette
di forma diversa, a seconda dell’uso cui sono destinate e spesso sono platinate (rivestite di platino
spugnoso che appare nero), con lo scopo di incrementare la superficie utile.
Nella seguente figura è mostrata una tipica cella conduttometrica; lateralmente è riportata una
schematizzazione della parte terminale contenente gli elettrodi aventi la forma precedentemente
proposta in modo tale da poter supporre che la nostra celletta interessi il volume unitario di
soluzione (1 cm3).
In questo modo è possibile confrontare la conduttanza elettrica dei vari elettroliti riferendosi sempre
allo stesso volume di soluzione.
OSSERVAZIONE
La geometria delle celle conduttometriche reperibili in commercio , di rado, per motivi tecnici, è
conforme a quella di un cubo perfetto di lato unitario, per cui è necessario tarare la cella prima di
effettuare delle misure conduttometriche.
La taratura di una cella consiste nell’effettuare con questa la misura della conduttanza di una
soluzione standard, generalmente KCl, di cui sia esattamente noto il valore di (p.es: a 250C, per
una soluzione 0,1N di KCl, =0,0128862 S cm-1); per confronto con questo valore e quello ottenuto
nella misura, si determina poi la costante di cella .
In pratica, dato che la conducibilità dipende linearmente dalla temperatura ed inoltre dato che
quest’ultima è generalmente diversa da quella riportata nelle tabelle, conviene applicare il metodo
dei minimi quadrati ai dati riportati in letteratura per ricavare la conducibilità specifica della
soluzione standard alla temperatura di esperienza. Ad esempio la seguente tabella riporta i dati
relativi a una soluzione standard 0,01 N di KCl.
T(0C)
(S cm-1)
0
0.000776
2
0.000824
4
0.000872
6
0.000921
8
0.00097
10
0.00102
12
0.00107
14
0.001121
16
0.001173
18
0.001225
20
0.001278
22
0.001332
25
0.001441
L’equazione che rappresenta la dipendenza di da T è la seguente:
tab = 0.000768+2.555e-5 * T
Supponiamo, ad esempio, di operare a 23,20C e di ottenere sperimentalmente il valore di spe=
0,0013 S cm-1 per la soluzione 0,01 N di KCl. Dalla equazione appena riportata, otteniamo per tab
il valore di 0,001361.
Per ricavare la costante di cella, basterà fare il rapporto tra la conducibilità misurata (spe) e quella
tabulata (tab), ottenendo un valore pari a 0,955 cm-1.
Per misurare la conduttività specifica è pertanto necessario utilizzare uno strumento che permette di
misurare la resistenza della soluzione offerta al passaggio di una debole corrente alternata (< 0,5
mA) a frequenza elevata (compresa tra 1000 e 2000 Hz). Non è possibile utilizzare una corrente
continua in quanto si avrebbe il fenomeno dell’elettrolisi con conseguente conversione dell’energia
elettrica in energia chimica. In tali condizioni la legge di Ohm, valida solo per circuiti ohmici, nei
quali l’unica dissipazione di energia elettrica è quella per effetto Joule, non è più rispettata.
L’utilizzazione di una frequenza elevata fa sì che i fenomeni di elettrolisi avvenuti nella frazione di
tempo in cui un elettrodo è ad es. positivo, si ripetano invertiti nella frazione di tempo successivo in
cui l’elettrodo è negativo.
La seguente figura mostra il principio di funzionamento dello strumento utilizzato per misurare la
resistenza della soluzione, denominato PONTE DI KOHLRAUSCH. Esso deriva dal ben noto
ponte di Wheatstone, utilizzato per misurare la resistenza di un conduttore metallico; l’unica
differenza deriva dal fatto che quest’ultimo è alimentato in corrente continua.
A
B
Per misurare la resistenza della soluzione con tale ponte si agisce sul resistore variabile R 1 sino a
che la differenza di potenziale esistente tra i punti A e B è nulla. Il condensatore variabile in
parallelo alla resistenza R1 va regolato in modo da compensare la componente capacitiva della cella
di misura.
La lettura della d.d.p. tra A e B viene effettuata tramite un voltmetro elettronico ad elevata
impedenza di ingresso tale da non falsare la misura.
Ad equilibrio raggiunto avremo che
R1 R x
R2 R3
ovvero
R x R1
R3
R2
Noti i valori di R2 e R3 e quello letto direttamente sul potenziometro R1, si può risalire al valore
della resistenza della soluzione , RX e quindi alla sua conducibilità specifica, dopo aver determinato
la costante di cella K
1
K
Rx
Nella pratica gli strumenti utilizzati sono già tarati in modo da avere una lettura diretta di , una
volta bilanciato il ponte.
Inoltre, in molti strumenti il bilanciamento del ponte avviene in modo automatico, per cui
l’utilizzatore si riduce semplicemente a leggere la conduttività su un display digitale, assieme alla
temperatura della soluzione.
CONDUCIBILITA’ MOLARE DI UNA SOLUZIONE ELETTROLITICA E SUA DIPENDENZA
DALLA CONCENTRAZIONE DELL’ELETTROLITA.
La conduttanza di una soluzione elettrolitica dipende dalla concentrazione degli ioni presenti in
soluzione, dalla loro carica, dalla loro mobilità e dalla temperatura.
Per correlare la conduttanza di un elettrolita con la sua concentrazione è necessario introdurre la
conduttività molare, m, che è direttamente legata alla conduttività specifica tramite la seguente
relazione:
m
1000
c
dove c è la concentrazione molare dell’elettrolita presente in soluzione e m viene espressa in
S x cm2 x moli-1.
La conduttività molare di un elettrolita sarebbe indipendente dalla concentrazione se la
conducibilità specifica fosse anch’essa proporzionale a tal concentrazione. In pratica invece si
trova che la conduttività molare dipende dalla concentrazione e, a seconda se l’elettrolita è forte o è
debole, si verificano due diversi comportamenti, come mostrato nella seguente figura:
a) ELETTROLITA FORTE
La conduttività molare ha un valore finito a diluizione infinita, denominato 0, e diminuisce
solo leggermente all’aumentare della concentrazione. Ciò è dovuto al fatto che l’interazione
tra coppie di ioni aumenta all’aumentare della concentrazione con conseguente diminuzione
della mobilità ionica.
Sperimentalmente si osserva che i dati sperimentali seguono la ben nota Equazione di
Onsager
0 k c
dove 0 è la conducibilità molare a diluizione infinita, c è la concentrazione molare espressa
in moli/litro e k è una costante che dipende dal solvente, dalla temperatura, dalla natura
dell’elettrolita e dal valore di 0.
Kohlrausch dimostrò un’altra importante proprietà degli elettroliti forti, denominata Legge
della migrazione indipendente degli ioni: a diluizione infinita la conduttività molare di un
sale può essere espressa come la somma delle conduttività dei singoli ioni:
0 0 0
dove e sono le conduttività molari limite dei singoli ioni e e sono,
rispettivamente, il n. di cationi e di anioni che formano l’elettrolita.
b) ELETTROLITA DEBOLE
La conduttività molare di un elettrolita debole mostra un comportamento completamente
diverso al variare della concentrazione. A concentrazioni elevate esso mostra una
conduttività relativamente piccola, mentre quest’ultima aumenta man a mano che la
concentrazione diminuisce, sino a raggiungere rapidamente un valore prossimo a quello di
un elettrolita forte, a diluizione infinita. Questo comportamento può essere spiegato dal fatto
che un elettrolita debole non è completamente dissociato, ma solo parzialmente e l’entità del
grado di dissociazione ha un effetto dominante sulla conduttività . All’aumentare della
diluizione l’equilibrio di dissociazione si sposta verso destra e quindi aumentano , il n. di
ioni e la conduttività molare.
Da misure sperimentali di conduttività in funzione della concentrazione c, Arrhenius derivò
la seguente relazione:
m 'm
dove m’ è la conduttività molare ipotetica se l’elettrolita fosse completamente dissociato.
Dato che negli elettroliti deboli la costante di dissociazione assume dei valori molto piccoli,
per cui e quindi la concentrazione degli ioni presenti in soluzione è molto piccola, allora
possiamo approssimare m con il valore limite 0 e scrivere
m 0m
Questa equazione è estremamente importante in quanto ci permette di determinare la
costante di dissociazione di un elettrolita debole mediante misure sperimentali di
conducibilità.
Per un elettrolita debole HA avente concentrazione molare c, la costante di dissociazione Kc
(trascurando i coefficienti di attività), è data dalla seguente relazione:
Kc
2 c
(1 )
, tramite opportuni passaggi si ottiene la seguente
0
espressione nota anche come Legge della diluizione di Ostwald :
Sostituendo al posto di il rapporto
m c
1
1
0
m m K c ( 0m ) 2
Misurando la conduttività specifica in funzione della concentrazione dell’elettrolita , si risale a
m e, nota 0 , si calcola la Kc, applicando il metodo dei minimi quadrati alla retta ottenuta
1
dall’equazione di Ostwald, dopo aver posto y
e x m c .
m
OSSERVAZIONE
Se si vogliono considerare le attività al posto delle concentrazioni in modo da ricavare la
costante di dissociazione KA ,avremo che
2,HA
2 c H A
Ka
Kc
(1 )
HA
1
avendo posto HA = 1. Passando ai logaritmi, avremo:
log K a log K c 2 log ,HA
Inoltre, essendo la soluzione molto diluita, varrà la legge limite di Debye Huckel per cui
log ,HA A z z I
dove A è una costante che dipende dal solvente e dalla temperatura della soluzione. Nel caso di
H2O a 250C, A=-0,509. Inoltre per un elettrolita monovalente HA avremo che
1
z+ =1 , z-=1 e I (ci zi2 ) c , per cui
2 i
log ,HA A c
Sostituendo nell’equazione del log Ka , avremo:
log K a log K c 2 A c
che può anche essere scritta come
log K c log K a 2 A c
Perciò, se Kc è stata determinata da misure di conducibilità diverse soluzioni diluite di HA secondo
quanto descritto precedentemente, allora da un grafico di log Kc in funzione di c , è possibile
ottenere Ka applicando i minimi quadrati alla suddetta equazione.