Slides

Laboratorio di chimica fisica - Esperienza EF
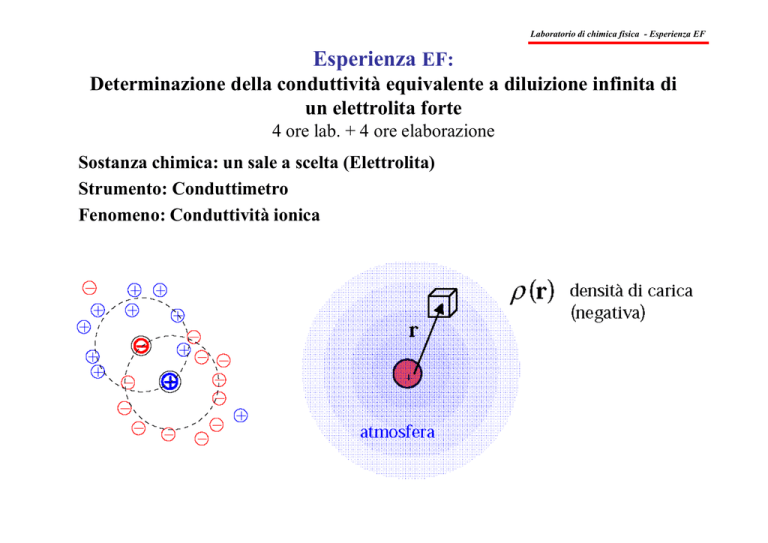
Esperienza EF:
Determinazione della conduttività equivalente a diluizione infinita di
un elettrolita forte
4 ore lab. + 4 ore elaborazione
Sostanza chimica: un sale a scelta (Elettrolita)
Strumento: Conduttimetro
Fenomeno: Conduttività ionica
Laboratorio di chimica fisica - Esperienza EF
Definizione di elettrolita
Elettroliti: composti in grado di dissociarsi in specie aventi carica opposta (ioni) quando
vengono disciolti in opportuni solventi → Soluzione elettrolitica.
Esempio: NaCl in H2O
Dissociazione di un generico elettrolita binario in soluzione:
Mν + Aν − ( solv ) = ν + M z + ( solv ) + ν - A z-( solv )
Qui tratteremo il caso di dissociazione “completa”. E’ sia il caso di “elettroliti forti”, che di
“elettroliti deboli” in concentrazioni basse
•Costante di equilibrio K della reazione di dissociazione: per un elettrolita binario Mν+ Aν− in
un dato solvente :
[ M z+ ] ν+ [A z - ] νK=
[Mν + Aν − ]
M ν + Aν − ↔ ν+ M z+ + ν- A z -
•E’ utile introdurre il grado di dissociazione α dato dal rapporto tra la frazione di composto
dissociata ed il totale:
α=
nd cd
=
nt
c
Laboratorio di chimica fisica - Esperienza EF
Elettroliti forti e deboli
•Per un elettrolita binario in cui valga z+=z- (ovvero v+=v-) è utile riscrivere la costante di
equilibrio in funzione del grado di dissociazione, ottenendo così la legge di diluizione di
Ostwald:
M ν + Aν − ↔ ν+ M z+ + ν- A z -
α=
nd cd
=
nt
c
[M ] = ν αc
[A ] = ν αc
Z+
Z−
+
α2
K=
c
1−α
−
[Mν + Aν − ] = (1 − α )c
•Nella pratica si dicono:
elettroliti forti quelli per cui vale α ~ l (ovvero K/c>10) a concentrazioni ordinarie
(diciamo ca. 0.1M)
elettroliti deboli quelli per cui vale α<1 (K/c<10-2) a concentrazioni ordinarie
Laboratorio di chimica fisica - Esperienza EF
Classificazione dei conduttori
Conduttori di 1a specie (metalli e semiconduttori): meccanismo di conduzione elettronico,
senza trasporto di materia associato
Conduttori di 2a specie (soluzioni elettrolitiche e sali fusi): meccanismo di conduzione
ionico, quindi con trasporto di materia
Altra classificazione in base alla 1a Legge di Ohm: proporzionalità tra d.d.p. applicata e
corrente osservata; il fattore di proporzionalità è la resistenza R del mezzo:
∆V = R i
Conduttori ohmici (metalli), che rispettano la relazione di linearità tra ∆V ed i
Conduttori non-ohmici (giunzioni p-n), che non rispettano la legge di Ohm
Le soluzioni elettrolitiche sono un caso particolare, in quanto sono non ohmici in DC ma
rispettano la legge di Ohm in corrente alternata (AC) ad alta frequenza (~1 kHz).
Laboratorio di chimica fisica - Esperienza EF
Conduttanza e conduttività
2a Legge di Ohm. Riguarda il legame tra resistenza e geometria del conduttore (di prima o
seconda specie):
lunghezza
l
R=ρ
S
sezione trasversale
resistività
(Ω cm)
L'inverso della resistenza è detto conduttanza G e si esprime in Ω-l , denominato anche
Siemens (simbolo S):
1
i
G= =
R ∆V
Analogamente la conduttività (o conducibilità specifica) χ è definita come l'inverso della
resistività ρ e si esprime in Ω-l cm-1 o in S cm-1:
χ =
1
ρ
S
G =χ
= κχ
l
ATTENZIONE: solo la conduttività è una proprietà intrinseca del conduttore (soluzione
elettrolitica), mentre la conduttanza dipende anche dalla geometria del conduttore.
Laboratorio di chimica fisica - Esperienza EF
Misure di conduttività (e conduttanza)
Le misure di conduttività di soluzioni elettrolitiche (conduttori non ohmici) richiedono di
operare in corrente alternata (>1kHz), al fine di evitare elettrolisi agli elettrodi, di ridurre la
resistenza dovuta al doppio-strato di cariche agli elettrodi e la polarizzazione agli elettrodi
Per ridurre ulteriormente la resistenza all’interfaccia, le celle conduttimetriche sono
costituite da due placchette in platino platinato (ad alta area superficiale)
Sreale >> Sgeom
La superficie reale non è misurabile, quindi la costante di cella deve essere determinata
mediante misura di conducibilità di una soluzione a conduttività nota (ad es. una soluzione
di KCl a titolo noto) alla temperatura specifica:
S
G = χ
= κχ
l
κ=
GRiferimento
χ Riferimento
χ = G /κ
Laboratorio di chimica fisica - Esperienza EF
Legame tra conduttività (grandezza misurabile) e proprietà molecolari
Equazione di Langevin per il moto di uno ione sotto l’effetto trascinante del campo elettrico.
Proiettiamo il moto lungo la direzione del campo elettrico (sul piano ad esso trasversale si ha
l’usuale moto browniano libero). Per ogni ione + e – di carica z+ e z- si ha:
massa*accelerazione
m±
dv±
= e z± E − ξ ± v±
dt
+ Γ ± (t )
forza di attrito che
si oppone al moto
forza elettrica esterna
forze d’urto casuali
(rumore bianco Gaussiano)
Mediando su un numero elevato di ioni si passa alle velocità medie v± . Tenendo presente
che il rumore Gaussiano ha media nulla, cioè Γ ± (t ) = 0 , si ha
m±
d v±
dt
= e z± E − ξ ± v±
Per tempi (sufficientemente) lunghi si giunge allo stato stazionario, cioè alla situazione di
accelerazione nulla (forza totale risultante da attrito e campo elettrico nulla) e di velocità di
migrazione media costante:
v± ∞ = e z± E / ξ ±
Si definisce mobilità ionica :
u± = e z± / ξ ± (espressa in cm2 V-1 s-1), quindi:
v±
∞
= u± E
Laboratorio di chimica fisica - Esperienza EF
Espressione microscopica della corrente elettrica i
In presenza di un campo elettrico, si avrà un flusso di ioni di tipo j che fluiscono, in
condizioni stazionarie, nell’unità di tempo attraverso l’unità di superficie ortogonale al
campo elettrico. Il corrispondente flusso di carica portata dagli ioni di tipo j è dato da
carica dello ione
(
δS
vj
j
∞
)
Flusso = (ez j ) N A × c j × 10−3 × v j
∞
carica per 1 mole
di ioni (NA il Numero
di Avogadro)
δl
densità di carica dovuta agli
ioni j espressa in Coulomb/cm3.
cj è la concentrazione molare,
quindi occorre il fattore 10-3
Per un elettrolita binario si hanno due tipi di portatori di carica e quindi i flussi possibili
sono due, ma in direzioni opposte:
Cationi: + eν + z N A c10
+
−3
Anioni: − eν − z N Ac10
−
v+
−3
v−
La corrente elettrica netta che passa nella cella conduttimetrica è data dalla somma dei flussi
di carica dovuti a tutti i tipi di ioni, positivi e negativi, presi in modulo e moltiplicati per l’area
effettiva S dell’interfaccia (placca della cella):
i=S F E
F = eN A = 96485 C/mol
costante di Faraday
∑c ju j z j /1000
j
Laboratorio di chimica fisica - Esperienza EF
Espressione microscopica della conduttività
Da G = i / ∆V , e tenendo presente che E = ∆V / l tra le placche della cella, si ricava
G = 10
−3

S
F  c ju j z j 

l
 j

∑
Dalla quale segue l’espressione “microscopica” della conduttività:


l
χ =G
= F  c j u j z j  /1000


S
 j

∑
Considerando il caso particolare di ioni generati dalla dissociazione di un elettrolita binario
forte in concentrazione molare c:
Mν + Aν − = ν + M z + + ν - A z-
G = c × 10−3 F (ν + u+ z+ + ν −u− z−
χ =G
l
S
) Sl
= c F (ν + u+ z+ + ν −u− z− ) /1000
In G e χ è presente una dipendenza primaria dalla concentrazione: aumentano all’aumentare di
c, cioè al crescere del numero di ioni trasportatori di carica per unità di volume.
Laboratorio di chimica fisica - Esperienza EF
Espressione microscopica della conduttività
Se la conduttività G dipendesse solo da c, sperimentalmente dovrei trovare una dipendenza
lineare
Misura per elettrolita binario
30
G (mS)
25
Fit lineare usando solo
i primi punti a c minore
20
15
10
5
0
0.00
0.05
0.10
0.15
0.20
0.25
0.30
c (M)
Invece è così solo a basse concentrazioni, dopo di che l’andamento subisce una deviazione
negativa rispetto all’andamento rettilineo (la soluzione conduce meno di quanto dovrebbe).
Infatti in G e χ è presente la dipendenza non solo dalla concentrazione c ma anche dalla
mobilità u dei portatori di carica (gli ioni)!
G = c × 10−3 F (ν + u+ z+ + ν −u− z−
χ =G
l
S
) Sl
= c F (ν + u+ z+ +ν −u− z− ) /1000
Questo risultato suggerisce che la mobilità ionica dipende dalla concentrazione di ioni in
soluzione.
Laboratorio di chimica fisica - Esperienza EF
Conduttività molare ed equivalente
Per eliminare la dipendenza ovvia da c e concentrarsi solo sulla dipendenza di u da c si
introduce la conduttività molare dell’elettrolita Λm (espressa in Ω-1 cm2 mol-1) definita come
Λm =
χ
c
1000
Fattore di conversione dimensionale da dm3 a cm3
Λm coincide con la conduttanza di 1 cm3 di soluzione 1 M dell’elettrolita in esame e serve a
confrontare la conduttività degli elettroliti in modo indipendente dalla concentrazione c.
Per un elettrolita che si dissocia secondo Mν + Aν −( solv ) = ν + M z + ( solv ) + ν -A z-( solv ) , tenendo presente
che deve valere ν + z+ = ν − z− = ν (elettroneutralità), con ν la “valenza” dell’elettrolita, si
definisce la conduttività equivalente dell’elettrolita Λ (espressa in Ω-1 cm2 g-equiv-1)
χ
Λ=
=
1000
ν
νc
Λm
Λ coincide con la conduttanza di 1 cm3 di soluzione 1 N dell’elettrolita in esame e serve a
confrontare tra loro le conduttività di elettroliti con diversa valenza in modo indipendente
dalla concentrazione c.
Laboratorio di chimica fisica - Esperienza EF
Espressione microscopica della conduttività molare
Considerando il caso particolare di ioni generati dalla dissociazione di un elettrolita binario
forte in concentrazione molare c:
Mν + Aν − = ν + M z + + ν - A z-
χ =G
Dalla definizione Λ m =
χ
l
S
= c F (ν + u+ z+ + ν −u− z− ) /1000
1000 si ricava
Λ m = F (ν +u+ z+ +ν −u− z−
)
c
Questa equazione mette in collegamento la grandezza accessibile sperimentalmente (Λm) con
le grandezze microscopiche dei singoli ioni (z ed u).
Si definiscono le conduttività equivalenti degli ioni:
λi = Fui
La conduttività molare dell’elettrolita binario viene quindi espressa come
Λ m = ν + z+ λ+ + ν − z− λ−
Λ
Dalla definizione di conduttività equivalente, Λ = m , e ricordando che ν + z+ = ν − z− = ν
ν
è la valenza dell’elettrolita, segue
Λ = λ+ + λ−
La conduttività equivalente di un elettrolita binario forte è pari alla somma delle conduttività
equivalenti degli ioni che esso genera.
Laboratorio di chimica fisica - Esperienza EF
Evidenza sperimentale della dipendenza di Λ da c
χ (Ω -1 cm -1)
6000
KI
4000
KOH
2000
Perchè che la conduttività equivalente non è
costante al variare di c:
Λ (Ω-1 cm2 g-equiv-1)
Le evidenze empiriche mostrano che la
conduttività non è linearmente proporzionale
alla concentrazione degli elettroliti:
150
KCl
140
130
BaCl2
CaCl 2
c(g-equiv/litro)
c(g-equiv /litro)
Non si osserva una crescita lineare
di χ con la concentrazione!
Λ non è costante con c, bensì
decresce al crescere di c!
“diluizione infinita” (c → 0)
χ=
χ =G
l
S
ν
1000
Λc
= c F (ν + u+ z+ + ν −u− z− ) /1000
Λ=
Λm
ν
=
χ
1000
νc
Λ m = F (ν +u+ z+ +ν −u− z−
)
Laboratorio di chimica fisica - Esperienza EF
Conduttività equivalente a diluizione infinita
Per discutere la dipendenza di u da c Partiamo da quanto è atteso a “diluizione infinita”
(c→0): soluzioni diluite ideali, assenza di interazioni tra gli ioni. E’ il modello di
Arrhenius (1884).
lim λi (c) = λi 0
Conduttività equivalenti dei singoli ioni a diluizione infinita
c →0
Conduttività equivalente a diluizione infinita per l’elettrolita binario
lim Λ (c) = Λ 0
c →0
Λ 0 = λ+0 + λ−0
Legge della migrazione indipendente degli ioni (Kohlrausch): a diluizione infinita i vari ioni
concorrono additivamente, e con contributi intrinseci λ i0 indipendenti dall’elettrolita che li ha
generati, a determinare Λ 0 .
Utilità: dato il solvente e la temperatura, da
0
valori tabulati di λi posso calcolare la
conduttività equivalente a diluizione infinita
dell’elettrolita!
Dati
in H2O a
25°C
Laboratorio di chimica fisica - Esperienza EF
Cosa accade per concentrazioni reali: atmosfera ionica
Il modello per le soluzioni elettrolitiche reali (non-ideali) che include le interazioni tra gli
ioni fa riferimento alla teoria di Debye-Hückel per la descrizione statistica della
distribuzione di carica attorno ad uno ione, che parte dal principio di elettroneutralità: uno
ione determina mediamente nel tempo una distribuzione di carica di segno opposto nel suo
intorno, con densità ρ (r ): è l’ “atmosfera ionica”.
ρ (r ) densità di carica (negativa)
in posizione r
r
+
atmosfera ionica
Se lo ione è immobile l’atmosfera ionica ha simmetria sferica; ρ (r ) decresce allontanandosi
dallo ione centrale. E’ dunque possibile identificare uno spessore “medio” d dell’atmosfera
ionica, che può essere quantificato attraverso la relazione seguente:
ρ (r )
d=
εk BT
1000e 2 N A ∑ c j z 2j
j
Esempio: per H2O a 25°C
con elettrolita uni-uni
valente in conc. 0.1 M si ha
un d pari a circa 10Å, per
0.01 M vale circa 30 Å
Laboratorio di chimica fisica - Esperienza EF
Cosa accade per concentrazioni reali: effetto elettroforetico
Quando si applica un campo elettrico E, localmente l’atmosfera ionica risente di una forza
per unità di volume pari a ρ (r )E .
Il campo elettrico induce una elettroforesi sull’atmosfera ionica.
Lo ione viene “trascinato” indietro dalla propria atmosfera ionica che così lo rallenta,
riducendone la velocità limite, quindi la mobilità ionica, quindi la conduttività equivalente
rispetto a quella a diluizione infinita:
Laboratorio di chimica fisica - Esperienza EF
Cosa accade per concentrazioni reali: effetto del tempo di rilassamento
Inoltre, all’atmosfera ionica va associata una struttura interna che fluttua e che risponde a
perturbazioni su tempi finiti. Quindi se lo ione centrale si muove, la sua atmosfera ionica
risulta permanentemente distorta e il baricentro di essa è “in ritardo” rispetto allo ione.
La separazione di carica dovuta all’asimmetria dell’atmosfera ionica produce una forza
frenante sullo ione.
Laboratorio di chimica fisica - Esperienza EF
Modello di Debye-Hucke-Onsager (D-H-O)
Globalmente, i due effetti sono considerati nel modello di Debye-Hückel-Onsager (D-H-O) per
la conduttività di un elettrolita forte in funzione della forza ionica.
Il modello predice una decrescita lineare di Λ in funzione di c .
Esprimendo tale legge in termini di concentrazione di elettrolita si ha:
Λ = Λ 0 − (k1 + k2 Λ 0 ) c
con k1 e k2 parametri dipendenti dalla temperatura e caratteristici del solvente e dell’elettrolita.
Ad esempio, per un elettrolita binario con z+ = z− = z si ha
1/ 2
z 2eF 2  2 
k1 =


3πη  ε RT 
z 3eF 2
k2 = w
24πε RT
con w = 2 − 2 = 0.586 (se z+ ≠ z− le espressioni sono più complesse!)
Λ (c )
Predizione:
Λ0
Funziona?
c
1/ 2
 2 


 ε RT 
Deviazione dalla D-H-O
A = 60.2
B = 0.229
C = 82.5
150
Laboratorio di chimica fisica - Esperienza EF
KCl
ο
Λ = 149.9
145
140
deviazioni a concentrazione
(forza ionica) elevata…
Λ
135
130
ο
ο
ο
ο
125
Λ = Λ − (Α + Β∗Λ )∗ c
120
Λ = Λ − (Α + Β∗Λ )∗ c1/2 + C*c
1/2
Debye-Hückel-Onsager
115
110
0
0.05
0.1
0.15
0.2
c
0.25
0.3
0.35
1/2
A concentrazioni elevate la forte non-idealità delle soluzioni (ad es. per formazione di coppie
ioniche) rende inadeguato il modello precedente; per il fit dei dati si utilizzano equazioni
empiriche del seguente tipo:
Λ = Λ 0 − (k1 ' + k2 ' Λ 0 ) c + k3 ' c
Λ + k1 '' c
= Λ 0 + k3 '' c + k4 '' c log c − k5 '' c 2
1 − k2 '' c
Notare come queste relazioni si
riducono alla Debye-Hückel-Onsager
per c tendente a 0…
Limite delle equazioni empiriche: fittano bene i dati ma manca un modello teorico che
interpreti i coefficienti che compaiono in esse!
Laboratorio di chimica fisica - Esperienza EF
Ambiti di uso frequente della conduttimetria
Titolazioni acido-base
G
Titolazioni di precipitazione o
complessazione di ioni
G
V
Le più importanti applicazioni analitiche conduttimetriche, nel settore ambientale, sono:
> contenuto di sali disciolti nelle acque destinate all’alimentazione umana
> controllo automatico in continuo del grado di inquinamento di acque superficiali (fiumi, laghi, ecc)
> controllo acque di falda
> controllo della salinità delle acque marine
> titolazioni acido-base a controllo conduttimetrico
> titolazione conduttimetrica di precipitazione dei cloruri nelle acque
> titolazioni conduttimetriche redox
> determinazione conduttimetrica dell’alcalinità totale in un’acqua
Esiste poi una classe di applicazioni per studi di cinetica (esperienza sulla cinetica di idrolisi di un
alogenuro alchilico nel corso di Chimica Fisica Industrale).