Trigonometria

Trigonometria
Trigonometria
Riassunto:
Le funzioni trigonometriche esprimono semplici relazioni geometriche fra angoli e (rapporti di) lunghezze.
Parole chiave:
Seno e Coseno | Calcolatore di Seno e Coseno | Seno e Coseno in un triangolo rettangolo | Seno e Coseno per qualsiasi angolo: la
circonferenza goniometrica | Segno di Seno e Coseno | Codominio di Seno e Coseno | Proprietà di Seno e Coseno | Il teorema di Pitagora
| Periodicità e (Anti-)simmetria | Angoli supplementari e complementari | Angoli doppi | Teoremi di Addizione per Seno e Coseno |
Tangente e Cotangente | Calcolatore di Tangente e Cotangente | Tangente e Cotangente in un triangolo rettangolo | Tangente e il
coefficiente angolare di una retta | Proprietà di Tangente e Cotangente | Angoli speciali | Radianti |
Seno e Coseno
Iniziamo con una domanda innocente: Dato un bastone di lunghezza 1 inclinato di un angolo α rispetto al piano orizzontale, quanto è
lunga la sua ombra quando il sole lo illumina verticalmente? Si consideri lo schizzo a lato: Il segmento rosso rappresenta il bastone,
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (1 di 16)07/11/2007 17.36.03
Trigonometria
la freccia rappresenta la luce che cade dall'alto. L'angolo α può essere scelto
arbitrariamente (nell'esempio a lato abbiamo α = 51°). Si cerca la lunghezza del segmento
verde.
A questo punto si ha una sorpresa che pone lo studente in una situazione completamente
nuova. Il problema non è solubile con le operazioni di calcolo che abbiamo visto fino ad ora!
Solo in casi eccezionali la lunghezza dell'ombra può essere espressa con numeri già noti
−
(ad esempio per α = 60° la lunghezza è 1/2, per α = 45° è 2 1/2), mentre se prendiamo
α = 51° otteniamo un numero (reale) che non si esprime in questo modo né in modo simile.
Pur non sapendo come calcolare la lunghezza dell'ombra per α = 51° (a titolo di esempio), è
chiaro che questa è univocamente determinata
dalla domanda posta sopra. Per ottenere una prima
approssimazione, possiamo fare un disegno
(possibilmente) preciso sullo stile di quello riportato più sopra e misurare la lunghezza del
segmento verde. Troveremo un valore di circa 0.63. Un procedimento di questo tipo è però
insoddisfacente dal punto di vista matematico. Quello che in ogni caso possiamo fare intanto è
dare un nome al risultato esatto: lo chiamiamo coseno.
La lunghezza del segmento verde si esprime con cos α oppure cos(α) e si legge "Cosen
alpha" oppure "Coseno di alpha". Poiché l'ombra è la lunghezza dell'immagine che il sole
"proietta" sulla terra, possiamo anche dire: cos α è la lunghezza della proiezione di un
segmento che − come nello schizzo qui a fianco a sinistra − è inclinato di angolo α e ha
lunghezza 1. Se α = 51°, come nel nostro esempio, scriveremo cos(51°). Il simbolo cos
(51°) rappresenta quindi un numero reale (circa uguale a 0.63), cos(60°) rappresenta un
altro numero reale (e cioè 1/2), ecc.
Analogamente possiamo illuminare il bastone con un raggio di luce in direzione orizzontale
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (2 di 16)07/11/2007 17.36.03
Trigonometria
e chiederci quanto sarà lunga la sua ombra proiettata su una parete verticale. Anche
questa lunghezza in generale non può essere espressa con uno dei metodi di calcolo a noi
già noti. La chiameremo Seno.
La lunghezza del segmento blu nello schizzo qui a fianco a destra si esprime con sin α
oppure sin(α) e si legge "Sen alpha" oppure "Seno di alpha". Anche questa volta si tratta
di una proiezione, adesso però ad opera di un raggio di luce orizzontale. Possiamo
anche interpretare sin α come la lunghezza apparente del bastone rosso sullo sfondo
visto da una grande distanza. Se ad esempio abbiamo α = 51°, scriviamo sin(51°).
Seno e Coseno (e altre grandezze che ricaveremo più sotto) si chiamano funzioni
trigonometriche. Il nome "funzione" deriva dal fatto, che a ciascun angolo α possiamo
assegnare i due numeri sin α e cos α. Da un punto di vista matematico non c'è niente di
eccezionale. Quando assegniamo a un numero x il suo quadrato scrivendo f(x) = x2 non
facciamo niente di diverso. La differenza rispetto a formare il quadrato consiste
soltanto nel fatto che il calcolo numerico di sin α e cos α per un angolo dato α è più
complicato. Per fortuna possiamo delegare questo compito a strumenti come il computer
o il calcolatore tascabile. Anche questi strumenti per la maggioranza degli angoli ci forniscono solo dei valori approssimati che però,
come nel caso dell'estrazione di radice, sono sufficientemente precisi per quanto riguarda le applicazioni pratiche.
Vi preghiamo quindi di accettare il fatto che in questo capitolo non troverete spiegazioni su come i calcolatori effettuano queste
operazioni. Ciò non ci impedisce comunque di utilizzare questi strumenti:
sin (
°)
=
cos (
°)
=
Provate a introdurre un angolo e a cliccare il segno = per ottenere il suo seno e coseno! Possiamo anche calcolare l'esempio visto
sopra (α = 51°) con grande precisione. Il nostro piccolo calcolatore ci dice che cos(51°) = 0.6293203910498375, e questa è la
lunghezza cercata dell'ombra proiettata sulla terra dal raggio verticale del sole. Per l'esattezza, anche questo è soltanto un valore
approssimato, ma nella pratica è sin troppo preciso. Se il nostro bastone rosso ad esempio è lungo un metro, possiamo senz'altro dire
che la lunghezza dell'ombra è 62.9 cm.
Seno e Coseno, così come tutte le altre funzioni trigonometriche che imparerete a conoscere in questo capitolo, hanno un ruolo
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (3 di 16)07/11/2007 17.36.03
Funzioni
Trigonometria
essenziale in matematica e in molte applicazioni. Fondamentalmente la loro importanza deriva dal fatto che nascono da problemi
geometrici semplici e molto generali (nel senso che si presentano frequentemente). Che il calcolo numerico sia complicato e venga
quindi delegato al computer o al calcolatore tascabile non dovrebbe distogliere dalla loro sostanziale semplicità. .
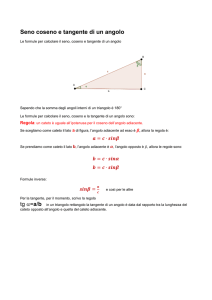
Seno e Coseno in un triangolo rettangolo
In linea di massima, adesso sappiamo che cosa sono il Seno e il Coseno di un angolo e vogliamo vedere come li possiamo
utilizzare. In ognuno dei disegni del paragrafo precedente troviamo un triangolo
rettangolo: l'abbiamo riportato nello schizzo qui a fianco a destra. Inoltre abbiamo
ruotato leggermente il tutto, visto che la posizione del triangolo nel piano non ha
nessuna importanza. Con l'aiuto di questo disegno possiamo caratterizzare le due
funzioni trigonometriche in maniera diversa:
In un triangolo rettangolo la cui ipotenusa ha lunghezza 1, sia α uno dei due angoli
acuti. Allora abbiamo che
●
●
sin α è la lunghezza del cateto opposto all'angolo α, e
cos α è la lunghezza del cateto adiacente all'angolo α.
Adesso consideriamo un triangolo rettangolo con lo stesso angolo α, ma con un'
ipotenusa di lunghezza non necessariamente uguale a 1.
Lo otteniamo "dilatando" o "riducendo" il nostro triangolo
originale in maniera tale da mantenere gli angoli. Si dice
che il triangolo originale e quello riportato qui a fianco a
sinistra sono simili. In entrambi i triangoli, il cateto opposto
all'angolo α) (blu) è più corto rispetto all'ipotenusa di un fattore sin α, e in entrambi i triangoli, il
cateto adiacente all'angolo (verde) è più corto rispetto all'ipotenusa di un fattore cos α. In
questo senso sin α e cos α possono essere interpretati come fattori di riduzione. Ciò può
essere dimostrato formalmente grazie al teorema di Talete. Vediamo quindi che in ogni
triangolo rettangolo vale:
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (4 di 16)07/11/2007 17.36.03
Inizio pagina
Trigonometria
sin α
cateto
opposto
=
(1)
ipotenusa
cos α
cateto
adiacente
=
(2)
ipotenusa
In molti libri Seno e Coseno vengono introdotti attraverso le proprietà (1) e (2). Potete cliccare sull' Applet qui a fianco per prendere più
confidenza con (1) e (2).
Dimostrazione
Applet: Definizione
Funzioni
Trigonometriche
Vogliamo illustrare come si utilizzano queste proprietà nei calcoli. Consideriamo il seguente problema geodetico: Come raffigurato
nello schizzo a fianco, la distanza diretta fra un punto di
osservazione e la vetta di un monte misura 3.7 km. La vetta
appare dal punto di osservazione sotto un angolo di 19.5°.
Quanto è alta la montagna?
Soluzione: Avete trovato il triangolo rettangolo nello schizzo?
Usiamo la relazione (1):
sin (19.5°)
=
h
.
3.7 km
Quindi h = sin(19.5°) × 3.7 km. Utilizzando il nostro calcolatore otteniamo sin(19.5°) = 0.3338, e quindi h = 0.3338 × 3.7 km = 1.24 km,
arrotondando il risultato ragionevolmente.
Seno e Coseno per qualsiasi angolo: circonferenza goniometrica
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (5 di 16)07/11/2007 17.36.03
Inizio pagina
Trigonometria
Le nostre definizioni date sopra di Seno e Coseno in realtà non sono ancora complete. Ricordiamoci: Abbiamo introdotto Seno e
Coseno come lunghezze dell'ombra di un bastone inclinato di lunghezza 1,
rispettivamente sotto un raggio di luce verticale (cos α) e un raggio di luce
orizzontale. (sin α). Lo raffiguriamo nel disegno qui a fianco, piazzando un estremo
del bastone (rosso) nell'origine di un sistema di coordinate cartesiane e
riportando "le ombre" (o meglio proiezioni) lungo gli assi cartesiani. L'angolo α si
misura relativamente all'asse orizzontale (delle ascisse) in senso antiorario.
Vediamo che si può aumentare l' angolo α ruotando il bastone rosso come una
lancetta di orologio (ma in senso antiorario). La punta della lancetta descrive un
cerchio (di raggio 1) detto "circonferenza goniometrica".
Possiamo ruotare la lancetta,
cioè il raggio rosso della
circonferenza goniometrica,
anche oltre la linea verticale. In
tal caso la posizione del raggio
è descritta, come nella figura a
fianco a sinistra, da un angolo
ottuso. Anche in questo caso
possiamo, come sopra, riportare le proiezioni sugli assi cartesiani e definire così
Seno e Coseno per un angolo ottuso. Qui adotteremo la seguente convenzione:
Un segmento orientato verso sinistra oppure verso il basso rispetto all'origine
sarà considerato negativo. L'angolo rappresentato nell'esempio a sinistra è 131°.
La lunghezza del segmento verde è circa 0.656. Il Coseno di questo angolo è
quindi circa −0.656, perciò negativo! Provate voi stessi con l'aiuto del nostro
calcolatore! sin(131°) invece è positivo (circa 0.755), poiché il segmento blu è
orientato verso l'alto rispetto all'origine.
Se continuiamo a ruotare il raggio rosso, possiamo rappresentare qualsiasi
angolo fra 0° e 360°, e in tutti questi casi il nostro procedimento ci fornirà un
valore univocamente determinato per il Seno e per il Coseno indicandoci anche il loro segno. Cliccando a fianco a destra otterrete una
rassegna sulle varie combinazioni di segno. Il segno di Seno e Coseno dipende dal quadrante in cui si trova il raggio che
rappresenta l'angolo α (i quadranti dividono il piano cartesiano in quattro parti delimitate dagli assi che vengono numerate in senso
antiorario da 1: " in alto a destra", 2: "in alto a sinistra" e 3: "in basso a sinistra" fino a 4: "in basso a destra").
Possiamo anche continuare a ruotare il raggio, ma non otterremo niente di nuovo: Un angolo di 370° non è diverso da 10° − per cui
anche le funzioni trigonometriche coincidono, ad es. sin(370°) = sin(10°). Anche ruotando il raggio in senso inverso e riducendo α fino
a raggiungere i numeri negativi non troveremo niente di nuovo: Un angolo di −10° non è diverso da 350°, per cui anche le funzioni
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (6 di 16)07/11/2007 17.36.03
Segno di Seno e Coseno
Trigonometria
trigonometriche coincidono, ad es. sin(−10°) = sin(350°). Il nostro calcolatore ve lo confermerà!
Come mai vogliamo definire Seno e Coseno per qualsiasi angolo, e perché lo facciamo così? Soprattutto per scopi pratici. Angoli fra
90° e 180° (cosiddetti ottusi, mentre quelli fra 0° e 90° sono detti acuti) sono presenti in molte applicazioni. E se il raggio rosso è
orientato verso destra e inclinato di 1° verso il basso, è molto più semplice indicare l'angolo con −1° piuttosto che con 359°. Questa
convenzione però ha anche delle conseguenze teoriche. Ad esempio la somma di due angoli è un angolo. Se α e β sono due angoli
(cioè descrivono due posizioni del nostro raggio), anche α + β sarà un angolo, poiché abbiamo ammesso qualsiasi valore. Basterà
ricordare che consideriamo identici gli angoli che differiscono di 360° (o di un multiplo di 360°).
Come vedremo nel prossimo paragrafo, con l'ausilio della circonferenza goniometrica possiamo dimostrare una serie di proprietà
basilari delle funzioni trigonometriche. La circonferenza goniometrica è uno strumento importante per la comprensione di Seno e
Coseno . Nell' Applet qui a fianco a destra potete modificare l'angolo e studiare il fenomeno interattivamente. La parte destra dell'
Applet mostra la raffigurazione grafica delle funzioni trigonometriche (per il concetto di grafico di una funzione si veda il capitolo
"Funzioni").
Applet
I grafici di
sin, cos e tan
Una delle proprietà che si ricavano dalla circonferenza goniometrica riguarda il codominio di Seno e Coseno: I valori di queste
funzioni non possono mai essere minori di −1 o maggiori di 1. Questo si deduce immediatamente dal fatto che le proiezioni del nostro
raggio (di lunghezza 1) sugli assi non possono essere più lunghe del raggio stesso. Concludiamo quindi che per qualsiasi angolo α si
ha
−1 ≤ sin α ≤ 1
e
−1 ≤ cos α ≤ 1
Proprietà di Seno e Coseno
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (7 di 16)07/11/2007 17.36.03
(3)
Inizio pagina
Trigonometria
Le funzioni Seno e Coseno sono fra le più importanti funzioni matematiche. Possiedono varie proprietà che vengono utilizzate sia nelle
applicazioni sia nella matematica pura. Parleremo adesso di alcune di queste proprietà.
Il Teorema di Pitagora
Forse vi stupirete di ritrovarlo qui. Consideriamo − come all'inizio di questo capitolo − un triangolo rettangolo, la cui ipotenusa ha
lunghezza 1. Qui a fianco abbiamo riportato una delle figure usate più sopra. (Tali triangoli si trovano
anche all'interno della circonferenza goniometrica del paragrafo precedente). Il Teorema di Pitagora ci dice
che in un triangolo rettangolo la somma dei quadrati (delle lunghezze) dei due cateti coincide con il
quadrato (della lunghezza) dell'ipotenusa. Applicandolo al triangolo qui a fianco, otteniamo per qualsiasi
angolo α l'identità
sin2α + cos2α = 1
(4)
Qui sin2α è un'abbreviazione per (sin α)2, in parole: "Seno quadrato di α". Questa formula non è altro che
una maniera − forse inizialmente poco usuale − di esprimere il Teorema di Pitagora. Ci fornisce una
semplice relazione fra Seno e Coseno. Se ad esempio − per un certo angolo α − conosciamo sin α,
possiamo dedurre
________
cos α = ± √ 1 − sin2α ,
(5)
dove il segno dipende dal quadrante in cui si trova il raggio che rappresenta l'angolo α nella circonferenza goniometrica (nel primo e
nel quarto quadrante +, altrimenti −).
Periodicità e (Anti-)simmetria
La circonferenza goniometrica ci mostra che Seno e Coseno sono funzioni periodiche: Quando a un angolo α sommiamo 360°, il
raggio ritorna nella stessa posizione di α. Quindi abbiamo
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (8 di 16)07/11/2007 17.36.03
Trigonometria
sin(α + 360°) = sin α
cos(α + 360°) = cos α.
(6)
Periodicità
Possiamo dire: Il periodo di entrambi le funzioni è 360°. Inoltre abbiamo
sin(−α) = −sin α
cos(−α) = cos α,
(7)
per cui Seno è una funzione antisimmetrica, mentre Coseno è una funzione simmetrica (per il significato esatto di questi due concetti
si clicchi qui a fianco oppure si veda il capitolo "Funzioni").
(Anti)simmetria
Identità con angoli supplementari e complementari
Possiamo anche dedurre identità che riguardano gli angoli la cui somma è pari a 90° (angoli complementari) oppure a 180° (angoli
supplementari) e anche gli angoli, la cui differenza è pari a 90° oppure 180°:
sin(90° − α) = cos α
cos(90° − α) = sin α
sin(α + 90°) = cos α
cos(α + 90°) = −sin α
sin(180° − α) = sin α
cos(180° − α) = −cos α
sin(α + 180°) = −sin α
cos(α + 180°) = −cos α.
I valori di Seno e Coseno per angoli arbitrari possono quindi essere dedotti dai valori per gli angoli compresi fra 0° e 90°.
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (9 di 16)07/11/2007 17.36.03
(8)
(9)
Dimostrazioni
(10)
(11)
Trigonometria
Angoli doppi
Se conosciamo il valore delle nostre funzioni trigonometriche per un angolo α, possiamo dedurre il valore per l' angolo doppio da
sin(2α) =
2 sin α cos α
(12)
cos(2α) =
cos2α − sin2α
(13)
Queste formule sono casi particolari di quelle che discutiamo nel prossimo punto.
Teoremi di Addizione per Seno e Coseno
Oltre alle relazioni fra Seno e Coseno discusse sopra, esistono altre identità che riguardano due angoli arbitrari. Sono note come
formule per l'addizione o teoremi di addizione. Ve le presentiamo senza dimostrazione (la dimostrazione più elegante usa i numeri
complessi). Per due angoli arbitrari α e β si ha sempre
sin(α + β) = sin α cos β + cos α sin β
(14)
cos(α + β) =
cos α cos β − sin α sin β
(15)
Se poniamo β = α, otteniamo (12) e (13).
Altre proprietà di Seno e Coseno si trovano cliccando qui a fianco.
Tangente e Cotangente
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (10 di 16)07/11/2007 17.36.03
Altre
proprietà
di Seno e Coseno
Inizio pagina
Trigonometria
Oltre a Seno e Coseno si usano anche altre funzioni da loro derivate. In particolare i quozienti di Seno e Coseno hanno un nome
proprio: Tangente e Cotangente: Ecco la definizione:
sin α
tan α
=
cot α =
(16)
cos α
cos α
sin α
1
=
tan α
.
(17)
Si noti che queste due espressioni sono reciproche e quindi strettamente legate: il loro prodotto è 1. (Su alcuni calcolatori tascabili
manca il tasto per Cotangente, che può essere calcolata come 1/Tangente). A volte invece di tan e cot si usano le abbreviazioni tg e
ctg. Ecco un piccolo calcolatore per queste due funzioni trigonometriche:
tan (
°)
=
cot (
°)
=
A differenza di Seno e Coseno, per certi angoli Tangente e Cotangente non sono definite: Si provi ad esempio a calcolare tan(90°)
oppure cot(0°). Il nostro calcolatore ci da "Infinity", avvertendoci che è stata tentata una divisione per zero . Dalle definizioni (16) e (17)
infatti deduciamo:
●
Se cos α = 0 (cosa che si verifica quando α = 90° oppure 270°, dove l'ultimo caso è equivalente a −90), il denominatore in (16)
●
diventa zero. In questi casi dunque tan α non è definita, mentre cot α = 0.
Se sin α = 0 (cosa che si verifica quando α = 0° oppure ±180°), il denominatore in (17) diventa zero. In questi casi dunque cot α
non è definita, mentre tan α = 0.
In tutti gli altri casi il nostro calcolatore ci fornisce dei numeri concreti che però adesso possono essere grandi a piacere.
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (11 di 16)07/11/2007 17.36.03
Applet
Definizione delle
funzioni
trigonometriche
Trigonometria
Tangente e Cotangente in un triangolo rettangolo
Anche Tangente e Cotangente possono essere interpretate come rapporti fra i lati in un triangolo rettangolo. Per le definizioni (16) e
(17) deduciamo da (1) e (2)
tan α
cateto opposto
=
cateto adiacente
cot α
cateto
adiacente
(18)
=
(19)
cateto opposto
Come esempio applicativo consideriamo il seguente problema geodetico: La vetta di un monte alto 1.24 km viene osservata sotto un
angolo di 19.5°. A che distanza si trova l'osservatore dalla proiezione sul piano della vetta del monte?
Soluzione: Avete trovato il triangolo rettangolo nello schizzo?
Usiamo la relazione (18):
tan (19.5°)
=
1.24 km
.
d
Quindi d = 1.24 km/tan(19.5°). Usando il calcolatore per
Tangente e Cotangente otteniamo tan(19.5°) = 0.3541,
dunque d = 1.24 km/0.3541 = 3.502 km (dove per scopi pratici in genere sarà sufficiente il valore approssimato d = 3.50 km).
Tangente e coefficiente angolare.
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (12 di 16)07/11/2007 17.36.03
Trigonometria
La Tangente ha un ruolo molto particolare poiché esprime la relazione fra il coefficiente angolare e l'angolo di pendenza di una retta.
Per determinare il coefficiente angolare di una retta, si raffigura , come nello schizzo
qui a fianco, il suo "triangolo di pendenza". Il quoziente k = ∆y/∆x si chiama
coefficiente angolare − ed ha il medesimo valore in ciascun triangolo di pendenza,
indipendentemente dalla sua grandezza. La Definizione (18) ci dice che il coefficiente
angolare è uguale alla tangente dell'angolo di pendenza che l'asse delle ascisse
forma con la retta stessa:
k = tan α.
(20)
Se ad esempio l'angolo di pendenza di una strada misura 12°, il coefficiente angolare è tan(12°), che è circa pari a 0 .21. Sul cartello
stradale che indica la pendenza della strada troveremo scritto "21%" (che possiamo leggere come "21 metri di dislivello per 100 metri
di distanza percorsi secondo la carta stradale"). Per una retta perpendicolare non ha senso parlare di coefficiente angolare, e ciò
corrisponde al fatto che tan(90°) e tan(−90°) non sono definite.
Proprietà di Tangente e Cotangente
Le relazioni elencate sopra per Seno e Coseno implicano una serie di proprietà utili per Tangente e Cotangente. Come per Seno e
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (13 di 16)07/11/2007 17.36.03
Applet
Il coefficiente angolare
(slope) di una retta
Trigonometria
Coseno possiamo utilizzare la circonferenza goniometrica, come raffigurata qui
a fianco. L'angolo α è individuato dal raggio (rosso). La Tangente di questo
angolo corrisponde alla lunghezza del segmento riportato sulla retta azzurra g.
Per la relazione (20) essa è pari alla pendenza del raggio, che nello schizzo è
stato prolungato con una linea tratteggiata fino a intersecare la retta g. Anche per
un angolo ottuso oppure negativo possiamo individuare la tangente sulla stessa
retta g. Con questo metodo possiamo anche determinare facilmente il segno per
un tale angolo. Nei casi α = 90° e α = −90° il raggio è parallelo alla retta g. Questa
è la spiegazione geometrica del fatto che la tangente non è definita per questi
angoli. A questo proposito si veda anche la parte sinistra dell'Applet qui a fianco.
Per la Cotangente valgono proprietà analoghe, scambiando i ruoli degli assi
cartesiani.
Applet
I grafici di
sin, cos e tan
Esercizio: Si riportino Seno, Coseno e Tangente in un'unica circonferenza
goniometrica. Si usi questo diagramma per dimostrare che il segmento sulla retta
g è la grandezza definita in (16). (Si notino i due triangoli simili).
Angoli speciali
Inizio pagina
Per certi angoli i valori delle funzioni trigonometriche possono essere espressi con le operazioni di calcolo usuali, in particolare con
radici quadrate. Riportiamo nella seguente tabella alcuni di questi angoli con i rispettivi valori:
α
sin α
cos α
tan α
cot α
0°
0
1
0
±∞
__
√3
__
√3
1
1
2
2
__
√2
1
30°
1
45°
2
__
√3
1
3
__
√2
1
1
2
Dimostrazioni
1
60°
2
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (14 di 16)07/11/2007 17.36.03
__
√3
1
2
__
√3
1
3
__
√3
Trigonometria
90°
1
0
±∞
0
180°
0
−
1
0
±∞
270°
−
1
0
±∞
0
In tutte le frazioni che contengono radici quadrate abbiamo reso razionale il denominatore. Il simbolo ±∞ sta a indicare che il valore
corrispondente non è definito.
Radianti
Ci sono varie misure angolari, cioè sistemi per misurare un angolo. Il metodo che probabilmente vi è più usuale è il sistema
sessagesimale, che si basa sulla divisione dell'angolo giro in 360 "gradi angolari".
Il numero 360 per l'angolo giro è scelto per motivi storici, ma dal punto di vista
matematico non é molto vantaggioso. Per molti scopi è molto più utile passare a un
altro sistema, la misura in radianti. Qui la grandezza di un angolo si misura come
lunghezza dell'arco corrispondente su una circonferenza di raggio 1. Ciò è
rappresentato nella figura qui a fianco: Invece di misurare l'angolo α in gradi, si usa
la lunghezza dell'arco azzurro come misura per la sua grandezza. L'angolo giro in
radianti è dato dalla circonferenza del cerchio di raggio 1, cioè da 2π.
Esempio: Un angolo di 60° (cioè un sesto dell'angolo giro) in radianti è pari a π/3,
cioè circa 1.0472. Vediamo subito gli svantaggi della misura in radianti: Angoli
"rotondi" come 30°, 45°, 60°, 90°, 180° e 360° vengono rappresentati da numeri
irrazionali. Nella migliore delle ipotesi sono dati da multipli razionali di π (come π/3
per 60°).
Quando un angolo è dato in radianti generalmente non si indica "l'unità di
misura" (cioè non si mette un simbolo come °). A volte si usa l'abbreviazione rad
(ad esempio 60° è π/3 rad, quindi circa 1.0472 rad), ma questo non è necessario.
La trasformazione da gradi in radianti e viceversa è molto semplice: Se α è un angolo dato in gradi, il suo valore in radianti è
2π × α/360°. Viceversa un valore in radianti va moltiplicato per 360°/(2π) per ottenere l'angolo in gradi.
La misura in radianti di un angolo può essere anche individuata con un cerchio di raggio arbitrario r. Se,
come nello schizzo qui a fianco, l'arco ha lunghezza s, allora l'angolo α in radianti è dato dal quoziente s/r.
Per il cerchio di raggio 1 (r = 1) ritroviamo la nostra definizione. Questa proprietà deriva dal fatto che tutti gli
"spicchi di torta" con lo stesso angolo α sono simili fra loro. Differiscono soltanto per la loro grandezza, ma
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (15 di 16)07/11/2007 17.36.03
Inizio pagina
Trigonometria
il rapporto fra le lunghezze s/r è costante per tutte queste figure, e può essere quindi usato come misura
dell'angolo.
Torniamo adesso alle funzioni trigonometriche. Alcune delle formule che abbiamo visto si riferivano alla
misura in gradi e possono ora essere tradotte in radianti. La periodicità di Seno e Coseno (6) in radianti è
data dalla formula
sin(α + 2π) = sin α
cos(α + 2π) = cos α.
(6b)
sin(π/2 − α) = cos α
cos(π/2 − α) = sin α
(8b)
sin(α + π/2) = cos α
cos(α + π/2) = −sin α
(9b)
sin(π − α) = sin α
cos(π − α) = −cos α
(10b)
sin(α + π) = −sin α
cos(α + π) = −cos α.
(11b)
e le relazioni (8)−(11) si traducono in
Anche le relazioni riguardanti Tangente e Cotangente e la tabella riportata sopra con i valori delle funzioni trigonometriche per alcuni
angoli speciali hanno una versione analoga in radianti (da consultare cliccando qui a fianco).
http://precorso.dicom.uninsubria.it/lezioni/Trigonometria.htm (16 di 16)07/11/2007 17.36.03
Tabella in radianti