Linee di Trasmissione:
Propagazione per onde
v+(z)
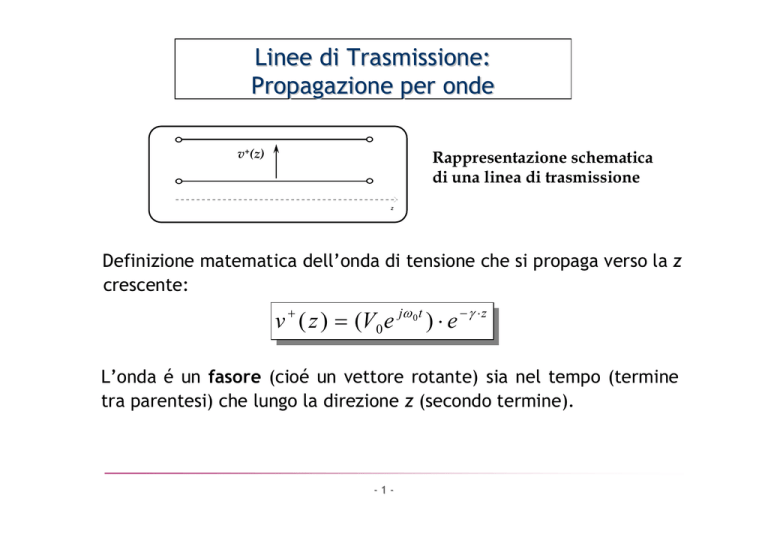
Rappresentazione schematica
di una linea di trasmissione
z
Definizione matematica dell’onda di tensione che si propaga verso la z
crescente:
v + ( z ) = (V0 e jω 0 t ) ⋅ e − γ ⋅ z
L’onda é un fasore (cioé un vettore rotante) sia nel tempo (termine
tra parentesi) che lungo la direzione z (secondo termine).
-1-
Significato della costante di
propagazione γ
Posto γ=α+jβ, si ha:
v + ( z ) = ⎡⎣ (V0 e jω t ) ⋅ e −α ⋅ z ⎤⎦ ⋅ e − j β ⋅ z
Costante di attenuazione α: Indica la rapiditá con cui si riduce
l’ampiezza dell’onda che si propaga. Si misura in Neper/m o in
dB/m (1Np = 8.686 dB)
Costante di fase β: Indica la rapiditá con cui cambia la fase
lungo la coordinata z (per t=cost). E’ legata alla lunghezza
d’onda e alla pulsazione dalla relazione β=2π/λ0=ω/ν (ν
rappresenta la velocitá di propagazione che dipende dal mezzo
che riempe la linea). β si misura in rad/sec.
-2-
Parametri primari della linea
Sezione Δz
L Δz
R Δz
C Δz
G Δz
Gli elementi R, L, C, G, sono detti parametri primari della linea di
trasmissione. Dipendono dalla struttura fisica della linea e dal mezzo che la
riempe.
Utilizzando i parametri primari si possono ricavare le equazioni che
governano la propagazione sulla linea (si impongono le equazioni di Kircoff
alla maglia e al nodo sul tratto di lunghezza infinitesima e si integra)
-3-
Parametri secondari
Impedenza Caratteristica (Zc): é l’impedenza che si vede all’ingresso di
una linea di lunghezza infinita (é presente solo l’onda che si propaga
verso le z crescenti)
Costante propagazione γ=α+jβ
Formule di calcolo in funzione dei parametri primari:
Zc =
L
,
C
α=
1R 1
+ G ⋅ Zc ,
2 Zc 2
β = ω ⋅ L⋅C
Queste relazioni sono valide per ω>> R/L, G/C; tali condizioni sono in pratica
sempre verificate se la frequenza operativa è superiore a qualche decina di
MHz.
-4-
Tensioni e correnti sulla linea
I(z)
V(z)
v+(z)
v-(z)
ZL
V ( z) = v+ ( z) + v− ( z) = V0+e− jβ z + V0-e+ jβ z
V0+ − jβ z V0- + jβ z
I ( z) = i ( z) + i ( z) = e − e
Zc
Zc
+
z
v+, i+: Onde Incidenti
−
v-, i-: Onde Riflesse
L’onda riflessa di tensione ha lo stesso segno dell’onda incidente; l’onda
riflessa di corrente ha segno opposto rispetto a quella incidente. Entrambe
sono legate tramite l’impedenza caratteristica della linea
Le onde riflesse si generano quando si introduce una disuniformitá nella
struttura fisica della linea (nel caso rappresentato é il carico). Per annullare
l’onda riflessa bisogna che ZL sia uguale a ZC.
-5-
Coefficiente di riflessione
Onda Riflessa V0− e + jβ z V0− + j 2 β z
Γ( z ) =
= + − jβ z = + e
= Γ0e + j 2 β z
Onda Incidente V0 e
V0
Propietá di Γ(z):
Il modulo non dipende da z (é costante lungo la linea)
La fase presenta, al variare di z, una periodicitá di λ/2
Il modulo é sempre minore di 1 quando il carico é passivo (la potenza
riflessa non puó superare quella incidente).
-6-
Andamento del |V(z)|
[
V (z) = v + (z) + v − (z) = v + (z) ⋅ 1 + Γ (z)
Vmax
|V|
V ( z ) = V 0+ 1 + Γ 0 ⋅ e +
Vmin
V 0+
Vmin
z
{
j2 βz
=
1 + 2 Γ0 ⋅ cos(2 β z) + Γ0
2
}
1
2
La tensione presenta un andamento periodico (stesso periodo di Γ) con
massimi e minimi che valgono rispettivamente:
V m ax ÷ 1 + Γ
,
V m in ÷ 1 − Γ
Si definisce Rapporto d’onda stazionaria (ROS) il rapporto tra queste
due tensioni:
ROS =
V m ax
V m in
-7-
]
Impedenza lungo la linea
I(z)
Z(z)
V(z)
ZL
1 + Γ( z)
V (z)
Z (z) =
= Zc
1 − Γ( z)
I (z)
z
Esiste una corrispondenza biunivoca tra il valore del coefficiente di
riflessione e l’impedenza vista in ogni sezione della linea (normalizzata
all’impedenza caratteristica)
OSSERVARE: L’impedenza é quella vista verso il carico!
Relazione inversa:
Z (z) − Zc
Γ(z) =
Z (z) + Zc
-8-
Impedenza di un tratto di linea
chiuso su una ZL generica
I(z)
V(z)
Zc , β
Vin
Z L + jZ c tan( βL )
Zin =
= Zc
I in
Z c + jZ L tan( βL )
ZL
L
Casi particolari:
ZL= 0 (corto circuito)
Z in =
Vin
L
= jZ c tan( β ⋅ L ) = jZ c tan(2π )
λ0
I in
ZL= ∝ (circuito aperto)
Z in =
Vin
L
= − jZ c cot( β ⋅ L ) = − jZ c cot(2π )
λ0
I in
-9-
Rappresentazione grafica di Γ
Γ é un numero complesso che puó
essere rappresentato sul piano x, y in
forma polare
|Γ|
•
Φ
1
Se il numero complesso Γ rappresenta
il coefficiente di riflessione su una
linea di trasmissione , il punto su piano
é sempre all’interno del cerchio a
raggio unitario
Γ
-1
1
-1
- 10 -
Rappresentazione grafica di Γ
Il coefficiente di riflessione su una linea
di trasmissione priva di perdite
si
rappresenta sul piano come un cerchio di
raggio pari al |Γ|. La fase varia di 360°
per uno spostamento di λ/2 sulla linea
d
c
Punti caratteristici:
Linea adattata Γ =0 ( centro della carta)
Circuito Aperto Γ =1 (a)
Corto circuito Γ =-1 (d)
Massimo di tensione sulla linea (b) (Γ reale e positivo)
Minimo di tensione sulla linea (c) (Γ reale e negativo)
- 11 -
|Γ|
b
a
Carta di Smith
Sul piano di rappresentazione di Γ si possono tracciare le curve che
rappresentano il luogo dei punti in cui la parte reale (o la parte
immaginaria) di zn=Z/Zc rimane costante:
⎧ Γ( z) + 1⎫
Re{Zin } = Re ⎨
⎬ = cost (r)
⎩ Γ( z) − 1⎭
⎧ Γ( z) + 1⎫
Im{Zin } = Im ⎨
⎬ = cost ( x)
⎩ Γ( z) − 1⎭
Queste curve sono dei cerchi, il cui raggio e centro dipendono dal
valore di r o x. La Carta di Smith é la rappresentazione grafica di
tali cerchi, che consente di risolvere, per via grafica, molti problemi
relativi all’impiego di linee di trasmissione nei circuiti a microonde.
- 12 -
Cerchio a x = 1
Verso il carico
Verso il generatore
Angolo di Γ (si misura in gradi
o in L/λ0
Cerchio a r = 1
Asse di riferimento
Rappresentazione delle ammettenze
sulla Carta di Smith
Impedenza nel punto Γ: zn =
1+ Γ
1− Γ
Γ
φ
Γ’
−Π+φ
Impedenza nel punto Γ’:
j ( −π +φ )
1 − Γ e jφ 1 − Γ 1
1 + Γ′ 1 + Γ e
zn′ =
=
=
=
=
jφ
j ( −π +φ )
′
1− Γ 1− Γ e
1+ Γ e
1 + Γ zn
Il punto diametralmente opposto presenta l’inverso dell’impedenza
del punto originale, cioè la sua ammettenza. La carta di Smith può
rappresentare indifferentemente Z o Y
- 14 -
Carta di Smith
Spostamenti a Γ costante
ZL
Γ0
0
Asse d
ΓL
Γ
x
d
⎧Γ ( x ) = Γ ⋅ e j 2 βx = Γ e j∠Γ0 ⋅ e j 4π ⋅(x λ )
0
0
⎪
⎨
− j 4π ⋅(d )
j∠Γ L
− j 2 βd
λ
⎪⎩Γ (d ) = Γ L ⋅ e
= ΓL e
⋅e
Spostamenti su linee senza perdite
0
Asse x
Spostamenti su cerchi a Γ costante
(circonferenze centrate nell’origine)
Spostamenti
¾ verso il carico Î spostamenti lungo x crescente
∠Γ ( x ) = ∠Γ 0 + 2 βx Î Rotazione antioraria
¾ dal carico Î spostamenti lungo x crescente
∠Γ ( x ) = ∠Γ L − 2 βd Rotazione oraria
NOTA: Γ (z) è una funzione periodica della distanza con periodo λ/2
- 15 -
Carta di Smith
Spostamenti a r o x Costanti
Spostamento a x costante
xL
r
ΓL
zL = rL + jxL
Γin
rL
zin = (rL + r) + jxL
rin = r+rL
Spostamento a r costante
xL
jx
ΓL
zL = rL + jxL
rL
zin = rL + j(xL + x)
- 16 -
Γin
xin = xL + x
Carta di Smith
Spostamenti a g o b Costanti
Carta delle Z
Spostamenti a b costante
ΓL
Γin
Γin
ΓI,in
yin = (gL + g) + jbL
gin =gL + g
ΓI,in
Γin
bL ΓI,L
- 17 -
gL
Γin
b
yin = gL + j(bL + b)
ΓL
L+
yL = gL + jbL
ΓL
bL
b
jb
gL
b
in =
b
Spostamenti a g costante
L+
b
bL ΓI,L
in =
yL = gL + jbL
b
g
gL
ΓL
Carta delle Y
bL
Carta di Smith
Esempio di Soluzione grafica
in
jX A
d
B
Zc
α=0
ΓL =
jB
ZL
Z L − Zc
= 0.62∠59.0°
Z L + Zc
Zc= 50 [Ω];
B= 0.05 [Ω-1]; (bn=2.5)
εr = [4];
X = -80 [Ω]; (xn=-1.6)
f0 = 3 [GHz];
d = 15 [mm]; (βd=108°)
ZL= 20 + j40 [Ω];
xin
(Zn=0.4+j0.8)
β=7.2 [°/mm]
ΓL
Γin ΓA
Γ B = 0.75∠ − 116.6°
2βL
2 βd = 40πd = 3.77 [rad] = 216.0°
ΓB
Γ A = 0.75∠27.4°
Γin = 0.51∠31.1° ⇒ Z in = Z c
1 + Γin
≅ 96 + j 68 [Ω ]
1 − Γin
- 18 -
bB