Due variabili aleatorie X ed Y si dicono in

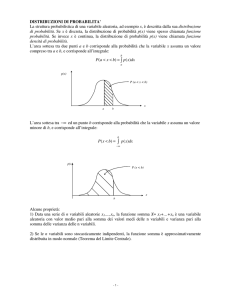
Due variabili aleatorie X ed Y si dicono indipendenti se comunque dati due numeri reali
a e b si ha
P {X = a, Y = b} = P {X = a}P {Y = b}
Una variabile aleatoria χ che assume i soli valori
1, 2, ..., n è detta binomiale con parametri
(n, p) se
p(i) = P {X = i} =
n
i
!
pi(1 − p)n−i.
Il valore atteso di una tale variabile binomiale
è np; la varianza è np(p − 1).
La variabile aleatoria Xi che vale 1 se l’i-esima
prova ha successo e 0 altrimenti, è una variabile
di Bernoulli. Chiaramente
X = X1 + .... + Xn
è una somma di variabili indipendenti.
Ebbene si ha
np = E[X] =
n
X
i=1
E[Xi] =
n
X
i=1
p = np.
Analogamente per la varianza
np(1 − p) = V ar(X) =
n
X
i=1
V ar(Xi).
Una variabile aleatoria χ che assume i soli valori
1, 2, ... è detta di Poisson con parametro λ
se
λi
−λ
,
p(i) = P {X = i} = e
i!
i = 0, 1, 2, ...
La variabile di Poisson ha valore atteso e varianza uguali a λ.
Se X1 e X2 sono due variabili di Poisson indipendenti con parametri λ1 e λ2, allora X1 +
X2 è una variabile di Poisson con parametro
λ1 + λ2
In generale la somma di due variabili aleatorie X ed Y ha media uguale alla somma delle
medie. Affinchè la medesima cosa capiti per
la varianza è necessario che le variabili in questione siano indipendenti. Se questo non capita,
interviene un fattore di correzione che dipende
da una quantità detta covarianza delle due
variabili:
V ar(X + Y ) = V ar(X) + V ar(Y ) + 2Cov(X, Y ).
Sia F un fenomeno per il quale:
1. La probabilità che F si verifichi esattamente
una volta in un intervallo di tempo pari ad h
sia uguale a λh + o(h).
2. La probabilità che F si verifichi due o più
volte in un intervallo di tempo pari ad h sia
uguale a o(h).
3. Siano n e j1, ..., jn numeri naturali. Dati n
intervalli di tempo disgiunti, indichiamo con Ei
l’evento “nel i-esimo intervallo di tempo F si è
verificato ji volte”. Ebbene gli eventi E1, ...,
En sono indipendenti.
Diremo allora che F è un processo di Poisson.
Il numero di volte N (t) che F si verifica in un
intervallo di tempo t è una variabile aleatoria
di Poisson con parametro λt. La costante λ,
che indica il numero di volte che F si verifica nell’unità di tempo, deve essere verificata
empiricamente.
In California si è valutato empiricamente che
si verificano due terremoti al mese. Supponiamo che il verificarsi di un terremoto soddisfi
le proprietà di un processo di Poisson.
Determinare la probabilità che vi siano almeno
quattro terremoti nei prossimi tre mesi e che
ve ne sia almeno uno nella prossima settimana.
Diciamo geometrica ogni variabile aleatoria
alla quale corrisponde una densità discreta del
tipo
p(n) = (1 − p)n−1p.
Corrisponde alla ripetizione di una prova, che
ha probabilità p di successo, sino a quando non
si ottiene un successo.
Determinare il valore atteso di una variabile
aleatoria geometrica.
Diciamo ipergeometrica ogni variabile aleatoria alla quale corrisponde una densità discreta
del tipo
p(i) =
m
i
!
N −m
n−i
N
n
!
!
per fissati N , n, m. Corrisponde alla estrazione
di n palline da un’urna contenente N palline,
di cui m bianche e le altre nere, e la variabile
aleatoria conta il numero di palline bianche
selezionate.
Diciamo continua una variabile aleatoria X
per la quale esiste una funzione non negativa f : R → R con la proprietà che per ogni
sottoinsieme misurabile B di R
P {X ∈ B} =
Z
B
f (x)dx
La funzione f è detta densità continua di X.
Il numero di ore che un computer funziona prima di rompersi è una variabile aleatoria continua con densità continua del tipo
(
f (x) =
x
− 100
λe
0
x≥0
x<0
Determinare il parametro λ e quindi determinare
la probabilità che il computer funzioni tra 50 e
150 ore prima di rompersi, e che funzioni per
meno di 100 ore.
Il valore atteso di una variabile continua con
densità continua f è
E[X] =
Z ∞
−∞
xf (x)dx.
Se g : R → R è una funzione e X una variabile
aleatoria continua, allora
E[g(X)] =
Z ∞
−∞
g(x)f (x)dx
Calcolare il valore atteso di eX con X variabile
aleatoria continua con densità continua
(
f (x) =
2x 0 ≤ x ≤ 1
0 altrimenti
La varianza di una variabile aleatoria continua
X è
V ar(X) = E[(X − µ)2].
Continua a valere la formula
V ar(X) = E[X 2] − (E[X])2.
Calcolare il valore atteso e la varianza della
variabile aleatoria continua X con densità continua
(
f (x) =
2x 0 ≤ x ≤ 1
0 altrimenti
Valgono ancora le formule
V ar(aX+b) = a2V ar(X),
E[aX+b] = aE[X]+b.
La somma di due variabili aleatorie continue X
ed Y ha media uguale alla somma delle medie.
Affinchè la medesima cosa capiti per la varianza è necessario che le variabili in questione
siano indipendenti. Se questo non capita, interviene un fattore di correzione che dipende
da una quantità detta covarianza delle due
variabili:
V ar(X + Y ) = V ar(X) + V ar(Y ) + 2Cov(X, Y ).
Diciamo che una variabile aleatoria X è uniformemente distribuita su un intervallo [α, β]
della retta reale se la sua densità continua f è
costante nell’intervallo [α, β] e 0 altrove. Necessariamente f deve valere 1/(β − α) nell’intervallo [α, β].
L’autobus numero 9 parte dalla stazione ogni 15 minuti a partire dai minuti 00. Se la
mattina uno arriva alla fermata in un momento uniformemente distribuito tra le 7 e le 7.30,
determinare la probabilità che attenda meno di
5 minuti la partenza dell’autobus. E qual’è la
probabilità che attenda la partenza per più di
10 minuti?
Diciamo che X è una variabile aleatoria normale con parametri (µ, σ 2) se la sua densità
continua è data da
1
f (x) = √
2π
2 /2σ 2
−(x−µ)
e
σ
,
x ∈ R.
I parametri µ e σ 2 rappresentano il valore atteso e la varianza della variabile normale.
Se X è una variabile normale con parametri µ
e σ 2, allora dati a, b ∈ R, la variabile Y = aX +b
è normale con parametri aµ + b e a2σ 2.
X −µ
In particolare Z =
è una variabile norσ
male con parametri 0 e 1; una tale variabile
normale è detta avere distribuzione standard.
La funzione di distribuzione di una variabile
aleatoria normale X con distribuzione standard
si indica tradizionalmente con Φ:
Z y
1 −x2/2
√ e
Φ(y) = P {X ≤ y} =
−∞ 2π
A pag. 203 del libro avete la tabella. Si tenga presente che Φ(−x) = 1 − Φ(x), pertanto
Φ(−2) = 1 − Φ(2).
Se Y è una variabile normale con parametri µ
e σ 2, con funzione di distribuzione F , allora
F (a) = P {Y ≤ a} = P {
a−µ
a−µ
Y −µ
≤
} = Φ(
)
σ
σ
σ
Sia X una variabile normale con parametri µ =
3 e σ 2 = 9. Determinare P {2 < X < 5}, P {X >
0} e P {|X − 3| > 6}.
Sia X una variabile continua uniformemente
distribuita su (0, 1). Si consideri la variabile
Y = X n. Determinare la funzione di distribuzione
e la densità continua di Y .
Diseguaglianza di Markov Se X è una variabile aleatoria che assume solo valori non negativi, allora per ogni a > 0 si ha
P {X ≥ a} ≤
E[X]
a
Diseguaglianza di Chebyshev Se X è una
variabile aleatoria con valore atteso µ e varianza σ 2, allora per ogni k > 0 si ha
σ2
P {|X − µ| ≥ k} ≤ 2
k
Teorema. (Legge debole dei grandi numeri)
Siano X1, ..., Xn variabili aleatorie indipendenti con la medesima funzione di distribuzione,
ciascuna con media e varianza finite E[Xi] = µ
e V ar(Xi) = σ 2. Allora, per ogni > 0 si ha
X1 + ... + Xn
P − µ ≥ → 0
n
n → ∞.
Teorema del limite centrale
Sia X1, X2, ... una sequenza di variabile aleatorie indipendenti con la medesima funzione di
distribuzione, con media µ e varianza σ 2. Allora la funzione di distribuzione di
X1 + ... + Xn − nµ
√
σ n
tende alla distribuzione normale standard per
n → ∞. Pertanto per −∞ < a < ∞, si ha che
per n → ∞
(
P
)
a
1
X1 + ... + Xn − nµ
−x2 /2 dx
√
e
≤
a
→
√
σ n
2π −∞
Z
Quando n è grande, una variabile binomiale X
con parametri (n, p) può essere approssimata
con una variabile normale XN con parametri
E[X] = np e V ar(X) = np(1 − p).
Determinare la probabilità che lanciando 40
volte una moneta si ottenga 20 volte testa.
Un astronomo deve misurare in anni luce la
distanza di una stella. Il subitaneo cambio di
condizioni atmosferiche, normali errori di misurazione etc. fanno si che più che una misura,
riesca ad ottenere una stima della reale distanza. Supponendo che diverse misurazioni siano
variabile aleatorie tra loro indipendenti, con la
medesima distribuzione, aventi media comune
d (la distanza reale della stella), e varianza comune pari a 4 anni luce, quante misure è necessario fare per poter essere ragionevolmente
sicuri che la distanza stimata abbia un margine
di errore inferiore a 0.5 anni luce?
Il numero di studenti che fanno il primo compitino di Matematica D in teledidattica è una
variabile aleatoria di Poisson con media 90.
Decido che se i partecipanti sono almeno 100,
ho bisogno di due aule, altrimenti ne basta
una sola. Qual’è la probabilità che vengano
utilizzate davvero due aule?
Lanciamo dieci dadi. Determinare la probabilità che la somma sia compresa tra 30 e 40
inclusi.
Teorema (Legge dei grandi numeri)
Sia X1, X2, ... una sequenza variabili aleatorie
indipendenti, con la medesima distribuzione,
tutte aventi media finita µ. Allora con probabilità 1,
X1 + ... + Xn
→µ
n
n → ∞.