punti matematica

1
Il sistema di riferimento cartesiano
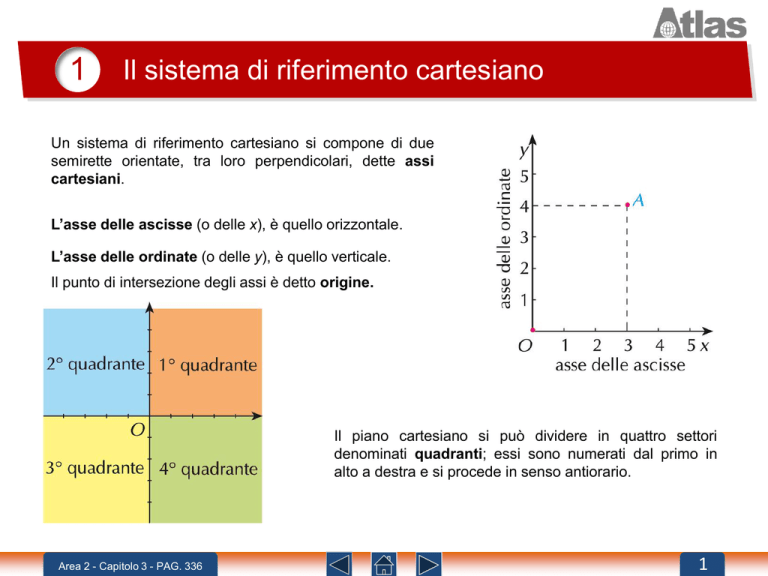
Un sistema di riferimento cartesiano si compone di due
semirette orientate, tra loro perpendicolari, dette assi
cartesiani.
L’asse delle ascisse (o delle x), è quello orizzontale.
L’asse delle ordinate (o delle y), è quello verticale.
Il punto di intersezione degli assi è detto origine.
Il piano cartesiano si può dividere in quattro settori
denominati quadranti; essi sono numerati dal primo in
alto a destra e si procede in senso antiorario.
Area 2 - Capitolo 3 - PAG. 336
1

2
La distanza tra due punti
Per determinare la distanza tra due punti nel piano cartesiano si possono presentare tre casi.
I caso I due punti hanno la stessa ordinata
Vogliamo calcolare la distanza tra i punti:
A2; 2 e B4; 2
AB  xB  x A  4  2  4  2  6  6

REGOLA. La misura del segmento AB con A e B aventi uguale ordinata è data dal valore assoluto
della differenza delle rispettive ascisse. In simboli:
AB  xB  x A
Area 2 - Capitolo 3 - PAG. 337
2

2
La distanza tra due punti
II caso I due punti hanno la stessa ascissa
Vogliamo calcolare la distanza tra i punti:
A2; 3 e B2;  4
AB  y B  y A  4 3  7  7


REGOLA. La misura del segmento AB con A e B aventi
uguale ascissa è data dal valore assoluto della differenza
delle rispettive ordinate. In simboli:
AB  y B  y A

Area 2 - Capitolo 3 - PAG. 337
3

2
La distanza tra due punti
III caso I due punti hanno ascisse e ordinate diverse
Vogliamo calcolare la distanza tra i punti:
A1;  2
e
B4; 2
Consideriamo il triangolo rettangolo ABC, ottenuto
tracciando da A e da B rispettivamente le parallele agli assi x
e y, e calcoliamo la lunghezza della sua ipotenusa con il
teorema di Pitagora:

AB  32  42  9 16  25  5
REGOLA. Per determinare la distanza tra due punti A e B si applica il teorema di Pitagora e si
calcola la misura dell’ipotenusa del triangolo rettangolo avente per cateti le proiezioni del segmento
AB sugli assi cartesiani. In simboli.
AB 
Area 2 - Capitolo 3 - PAG. 338
xA  xB   y A  y B 
2
2
4
2
Le coordinate del punto medio di un segmento
REGOLA. Le coordinate del punto medio M di un segmento AB sono date dalle semisomme
delle ascisse e delle ordinate degli estremi del segmento. In simboli:
x A  xB y A  y B 
M 
;

2
2


Vogliamo calcolare le coordinate del punto medio M del
segmento di estremi
A2; 3
 e B 4;  5


Applichiamo direttamente la formula:


2  4 2  4 2
xM  


 1
2
2
2
yM
3  5 3  5 2



 1
2
2
2
Area 2 - Capitolo 3 - PAG. 338
5
3
Il concetto di funzione
DEFINIZIONE. Una relazione R da un insieme A verso un insieme B, che associa ad ogni elemento
di A uno ed uno solo elemento di B, prende il nome di funzione.
Il dominio di una funzione è l’insieme degli elementi a  A che hanno un’immagine in B.
Il codominio di una funzione è l’insieme degli elementi b  B che hanno una controimmagine in A.


Area 2 - Capitolo 3 - PAG. 339
6
3
Le funzioni empiriche
Consideriamo la quantità di pioggia caduta nei vari mesi dell’anno in una località e disegnamone il
grafico.
100
mm di pioggia
90
80
70
60
50
40
30
20
10
Dicembre
Novembre
Ottobre
Settembre
Agosto
Luglio
Giugno
Maggio
Aprile
Marzo
Febbraio
Gennaio
0
Mesi dell’anno
Una funzione di questo tipo viene detta empirica perché non è possibile stabilire un legame fra il
mese dell’anno e i millimetri di pioggia.
Area 2 - Capitolo 3 - PAG. 341
7
3
Le funzioni matematiche
Indicando con x gli elementi dell’insieme A (dominio) e
con y gli elementi dell’insieme B (codominio) possiamo
dire che
DEFINIZIONE. La funzione matematica è un tipo di
funzione in cui il variare della y rispetto alla x avviene
sulla base di un meccanismo fisso che può essere
espresso mediante una precisa formula matematica.
Per mezzo di questa formula i valori assunti dalla y (in
seguito al variare della x) possono essere determinati
con precisione e sicurezza.
In simboli possiamo scrivere che
y  f x 
e si legge << y uguale effe di x >>
f :x y
e si legge << f è tale da portare x in y >>
oppure

Area 2 - Capitolo 3 - PAG. 341
8
4
La funzione di proporzionalità diretta
DEFINIZIONE. Due grandezze si dicono direttamente proporzionali se raddoppiando, triplicando,
dimezzando … l’una, raddoppia, triplica, si dimezza … anche l’altra.
DEFINIZIONE. Due grandezze sono direttamente proporzionali se il loro rapporto è costante.
In generale se x e y sono una qualsiasi coppia di valori corrispondenti, indicata con m la costante di
proporzionalità diretta abbiamo:
y
m
x
quindi
y  mx
con m ≠ 0
La formula precedente rappresenta la funzione di proporzionalità diretta; in essa m rappresenta il
coefficiente di proporzionalità diretta.

Area 2 - Capitolo 3 - PAG. 343

9
4
Rappresentazione cartesiana della funzione y = mx
Consideriamo la funzione di proporzionalità diretta di equazione
y  3x
in cui il coefficiente di proporzionalità è 3.

Il grafico della funzione y = 3x è una retta passante per l’origine degli
assi, quindi generalizzando possiamo dire che:
DEFINIZIONE. La legge di proporzionalità diretta è rappresentata nel
piano cartesiano da una retta passante per l’origine.
Area 2 - Capitolo 3 - PAG. 344
10
4
Considerazioni sul coefficiente di proporzionalità diretta
PROPRIETÀ. La funzione y = mx rappresenta sempre
una retta passante per l’origine, inoltre:
 se m > 0 la retta appartiene al 1° e 3° quadrante;
 se m < 0 la retta appartiene al 2° e 4° quadrante.
Area 2 - Capitolo 3 - PAG. 345
11
4
Considerazioni sul coefficiente di proporzionalità diretta
PROPRIETÀ. Nella funzione y = mx:
 se m = 1 la retta è la bisettrice del 1° e 3° quadrante;
 se m = −1 la retta è la bisettrice del 2° e 4°
quadrante.
Area 2 - Capitolo 3 - PAG. 345
12
4
Considerazioni sul coefficiente di proporzionalità diretta
PROPRIETÀ. Maggiore è il valore del coefficiente angolare m (in valore assoluto) tanto più
l’inclinazione della retta si avvicina all’asse y.
Area 2 - Capitolo 3 - PAG. 346
13
5 La retta nel piano cartesiano
Rappresentiamo nel piano la funzione y  2x  3
Più in generale:
 del tipo y = mx + q (con m e
PROPRIETÀ. Ogni funzione
q costanti) rappresenta l’equazione di una retta; m è il
coefficiente angolare e q rappresenta l’ordinata
all’origine.
È importante notare che l’equazione generica di una retta
y = mx + q non è più una funzione di proporzionalità
diretta.
Area 2 - Capitolo 3 - PAG. 348
14
5 Le equazioni di rette particolari
Rette parallele all’asse x
PROPRIETÀ. y = k (con k costante) è l’equazione di una retta
parallela all’asse delle x.
 Se k > 0 le rette parallele all’asse x appartengono al semipiano
positivo delle ordinate;
 se k < 0 le rette appartengono al semipiano negativo delle
ordinate;
 se k = 0 la retta coincide con l’asse x e la sua equazione diventa
y = 0; diremo allora che y = 0 è l’equazione dell’asse x.
Area 2 - Capitolo 3 - PAG. 348
15
5 Le equazioni di rette particolari
Rette parallele all’asse y
PROPRIETÀ. x = h (con h costante) è l’equazione di una
retta parallela all’asse delle y.
 Se h > 0 le rette parallele all’asse y appartengono al semipiano
positivo delle ascisse;
 se h < 0 le rette appartengono al semipiano negativo delle
ascisse;
 se h = 0 la retta coincide con l’asse y e la sua equazione diventa
x = 0; diremo allora che x = 0 è l’equazione dell’asse y.
Area 2 - Capitolo 3 - PAG. 349
16
5 Le equazioni di rette particolari
Rette tra loro parallele
PROPRIETÀ. Due rette parallele hanno lo stesso coefficiente
angolare. In simboli, date:
r : y  mx  q
r || s

s : y  mx  q
se e solo se
m  m


Area 2 - Capitolo 3 - PAG. 349

17
5 Le equazioni di rette particolari
Rette tra loro perpendicolari
PROPRIETÀ. Due rette sono perpendicolari se il
coefficiente angolare della prima è l’antireciproco dell’altro.
In simboli, date
r : y  mx  q
rs
se e solo se
s : y  mx  q
m
1
ovvero m  m 1
m


Area 2 - Capitolo 3 - PAG. 349

18
5 L’intersezione di una retta con gli assi cartesiani
REGOLA. Le coordinate dei due punti di intersezione di
una retta di equazione y = mx + q con gli assi x e y si
ottengono ponendo in essa y = 0 e x = 0 e calcolando i
valori corrispondenti dell’ascissa e dell’ordinata dei due
punti.
Troviamo, ad esempio, i punti d’intersezione con gli assi
della retta
y 
5
x5
2




 se x  0  y  5  A 0 ; 5
 se y 
0  x 2  B 2; 0
Area 2 - Capitolo 3 - PAG. 350
19
5 Equazioni di rette
FORMULA. La relazione che permette di determinare l’equazione di una retta passante per un
punto P(x0; y0) e di coefficiente angolare m è
y  y 0  m  x  x 0 

FORMULA. La relazione che permette di determinare l’equazione di una retta passante per i punti
A(x1; y1) e B(x2; y2) è
y  y1
x  x1

y 2  y1 x2  x1

Area 2 - Capitolo 3 - PAG. 350
20
6
La funzione di proporzionalità inversa
DEFINIZIONE. Due grandezze si dicono inversamente proporzionali se raddoppiando, triplicando,
dimezzando … l’una, si dimezza, diventa un terzo, raddoppia … l’altra.
DEFINIZIONE. Due grandezze sono inversamente proporzionali se il loro prodotto è costante.
In generale se x e y sono una qualsiasi coppia di valori corrispondenti, indicata con k la costante di
proporzionalità inversa, abbiamo:
y
xy  k
k
x
con x  0
La formula precedente rappresenta dunque la funzione di proporzionalità inversa; in essa k è il
coefficiente di proporzionalità inversa.

Area 2 - Capitolo 3 - PAG. 353


21
6
La rappresentazione cartesiana della funzione xy=k
Consideriamo la funzione di proporzionalità inversa di
equazione
16
y
x
Il grafico è
un ramo di curva che prende il nome di
iperbole equilatera. In generale:
DEFINIZIONE. La legge di proporzionalità inversa è
rappresentata nel piano cartesiano da un’iperbole
equilatera.
Area 2 - Capitolo 3 - PAG. 354
22
7
La proporzionalità quadratica e la parabola
DEFINIZIONE. Due grandezze x e y sono in
proporzionalità quadratica quando la relazione che le
lega si può esprimere con una formula del tipo:
y  ax 2
La formula precedente rappresenta la funzione di
proporzionalità quadratica; in essa a prende il nome di
di proporzionalità quadratica.
coefficiente
La funzione di proporzionalità quadratica è rappresentata
nel piano cartesiano da una curva, chiamata parabola, i
cui punti godono della seguente proprietà:
PROPRIETÀ. I punti di una parabola hanno la stessa distanza da un punto fisso (F) chiamato
fuoco, e da una retta fissa (d), chiamata direttrice.
Area 2 - Capitolo 3 - PAG. 357
23
7
La proporzionalità quadratica e la parabola
DEFINIZIONE. Una funzione del tipo y = ax2 (con a ≠ 0) è l’equazione di una parabola avente
come asse di simmetria l’asse y e come vertice l’origine degli assi.
In particolare
• se a > 0 la parabola ha la concavità verso l’alto;
• se a < 0 la parabola ha la concavità verso il basso.
Area 2 - Capitolo 3 - PAG. 358
24