Equilibrio con tassa In presenza di una tassa, è

Equilibrio con tassa
In presenza di una tassa, è importante ricordare che non esiste un solo prezzo
di equilibrio, ma ne esistono due: il prezzo di o¤erta, ovvero il prezzo che
riceve il venditore, e il prezzo di domanda, ovvero il prezzo pagato dal consumatore. I due prezzi sono legati dalla relazione:
p d = ps + t
(1)
Si noti che, in equilibrio, mentre i prezzi sono due, la quantità è una sola,
quindi non bisogna fare confusione!
Distinguiamo due casi, a seconda che la tassa gravi sul venditore o gravi
sul consumatore. Si ricordi che i due casi portano allo stesso risultato, quindi
quando il problema non speci…ca su quale dei due agenti gravi la tassa, è indifferente quale dei due metodi utilizzare.
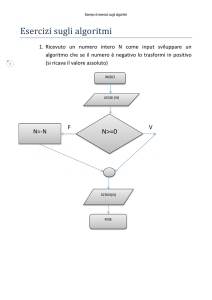
Caso 1. Quando la tassa è a carico del venditore, la curva di o¤erta trasla
verso l’alto. L’incrocio tra domanda e o¤erta determina il prezzo di domanda.
Il prezzo di o¤erta si determina poi facilmente dalla relazione (1).
P
offerta dopo la tassa
Prezzo di domanda
tassa
offerta prima della tassa
Equilibrio prima della tassa
Prezzo di offerta
domanda
Q
Gra…co 1
1
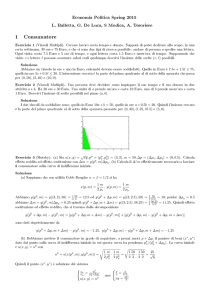
Caso 2. Quando la tassa è a carico del compratore, la curva di domanda
trasla verso il basso. Stavolta l’incrocio tra domanda e o¤erta determina il
prezzo di o¤erta, mentre quello di doamanda si ricava di nuovo dalla relazione
(1).
P
offerta
tassa
Prezzo di domanda
Equilibrio prima della tassa
Prezzo di offerta
domanda prima della tassa
domanda dopo la tassa
Q
Gra…co 2
Analiticamente, in entrambi i casi, si tratta di risolvere il sistema:
Qd = Qs
p d = ps + t
Dove, nel caso di imposta gravante sul consumatore, si sostituisce il valore
di pd , ricavato dalla seconda equazione, nel primo membro della prima e si
ottiene il prezzo di o¤erta, mentre nel caso di imposta gravante sul venditore si
sostituisce il valore di ps ricavato dalla seconda equazione nella secondo membro
della prima e si ottiene il prezzo di domanda.
Naturalmente, essendo un sistema, i due metodi sono equivalenti. Quello
che importa è indicare sempre il prezzo di o¤erta e il prezzo di domanda con
le notazioni Ps e Pd , in modo da avere sempre ben chiaro quale prezzo si sta
ottenendo, e poi utilizzare la seconda relazione per calcolare l’altro prezzo di
equilibrio.
2
Esercizio
Trovare l’equilibrio nel mercato del bene x in cui le funzioni di domanda e
di o¤erta sono:
qd = 300 2pd
qs = ps 60
e calcolare come cambia l’equilibrio con l’imposizione di una tassa pari a 30.
Soluzione
L’equilibrio senza tassa è:
300
2p = p
60
da cui si ricava:
p = 120
q = 60
In presenza di una tassa, il sistema da risolvere è:
300
2pd = ps 60
pd = ps + 30
Risolvendo il sistema si ottiene
ps = 100
pd = 130
q = 40
[Si noti che a seconda che si sostituisca nella prima equazione il valore di pd o
ps , si ottiene l’equazione che rappresenta l’equilibrio alternativamente in cui la
tassa grava sul consumatore o sul venditore. Cioè, se sostituiamo pd = ps + 30
nella prima, otteniamo:
300
2(ps + 30) = ps
60
che rappresenta l’equilibrio nel caso in cui l’imposta grava sul consumatore
(rappresentato nel gra…co 2), e infatti consente di ottenere il prezzo di o¤erta
(ps = 100), mentre il prezzo di domanda è dato dalla relazione pd = ps + t =
100 + 30 = 130
Se invece si fosse sostituito il valore ps = pd
300 2ps = (pd 30) + 60
3
30, si sarebbe ottenuto:
che rappresenta l’equilibrio nel caso in cui l’imposta grava sul venditore
(gra…co 1), e infatti consente di ottenere il prezzo di domanda (pd = 130),
mentre il prezzo di o¤erta sarà dato dalla relazione ps = pd t = 130 30 = 100
Come si può notare i risultati ottenuti sono gli stessi, quindi risulta indi¤erente su chi grava l’imposta e il modo con cui si risolve il sistema.]
Calcolo del surplus.
Per il calcolo del surplus senza tassa, è su¢ cente rappresentare l’equilibrio
iniziale e calcolare le intercette delle curve con l’asse delle ordinate:
P
s
150
surplus consumatore
120
E
surplus venditore
60
d
Q
60
Gra…co 3
Il surplus del consumatore è dato dall’area del triangolo superiore:
Sc = (150 120)(60)=2 = 900
Mentre il surplus del venditore è dato dall’area del triangolo inferiore:
Sv = (120
60)(60)=2 = 1800
Naturalmente il suplus totale è dato dalla somma dei due surpus:
Stot = Sc + Sp = (900 + 1800) = 2700
Per rappresentare il surplus in presenza di tassa, dobbiamo aggiungere al
gra…co 3 i prezzi di o¤erta e di domanda e la nuova quantità scambiata in
presenza di tassa.
4
P
150
s
surplus consumatore
130
perdita di surplus del consumatore
E
120
perdita di surplus del venditore
100
surplus venditore
60
d
40
Q
60
Gra…co 4
Stavolta individuiamo le seguenti aree:
1. Il triangolo in alto è il nuovo surplus del consumatore:
Sc = (150
130)(40)=2 = 400
2. Il triangolo in basso è il nuovo surplus del venditore:
Sv = (100 60)(40)=2 = 800
3. Il primo trapezio dall’alto è la perdita di surplus del consumatore causata
dalla tassa. La sua area la si calcola per di¤erenza tra il surplus prima della
tassa e dopo la tassa:
Pc = 900
400 = 500
4. Il secondo trapezio dall’alto, è la perdita di surplus del venditore causata
dalla tassa. La sua area la si calcola per di¤erenza tra il surplus prima della
tassa e dopo la tassa:
Pv = 1800
800 = 900
5
5. L’ammontare del prelievo …scale è dato dal rettangolo delimitato dal
prezzo di o¤erta (100), di domanda (130) e la nuova quantità scambiata (40),
ossia dal prodotto della tassa unitaria per le quantità scambiate:
P F = QT = 40 30 = 1200
6. I due triangoli più piccoli all’interno dei due trapezi rappresentano la
perdita sociale netta, e si calcolano come di¤erenza tra il surplus totale inziale
(Sc + Sv ) e il surplus totale dopo la tassa, comprensivo del gettito …scale (Sc +
Sv + P F ):
PSOC = 2700
400
800
1200 = 300
___________________________________________________
Tassa ad valorem
Nel caso di una tassa ad valorem, rimane valido tutto il discorso fatto sino
ad ora, solo che le traslazioni della domanda (verso il basso) e dell’o¤erta (verso
l’alto) non sono più parallele e il sistema da risolvere diventa:
Qd = Qs
pd = ps (1 + t)
dove t stavolta è la tassa espressa in percentuale. Risolvendo il sistema
si ottengono i prezzi di domanda e o¤erta e la nuova quantità scambiata. Si
noti soltanto che nel caso si voglia isolare ps nella seconda equazione, si ottiene
ps = pd =(1 + t):
esempio
Nell’esercizio precedente si ipotizzi una tassa ad valorem t = 10%:Richiamiamo
le equazioni di domanda e o¤erta originarie:
qd = 300 2pd
qs = ps 60
Il sistema diventa:
300 2pd = ps 60
pd = ps (1 + 0; 10)
Che, risolto indi¤erentemente rispetto a ps o pd , consente di ottenere:
ps = 112; 5
pd = 123; 75
q = 52; 5
La rappresentazione dei surplus è identica all’esempio precedente.
6
___________________________________________________
Sussidi
In presenza di sussidi il discorso è simmetrico. Nel caso di sussidio unitario
s, il sistema diventa:
Qd = Qs
p s = pd + s
che di¤erisce da quello con tasse per il fatto che nella seconda equazione il
ruolo di ps e pd è invertito.
Nel caso di sussidio ad valorem , il sistema è:
Qd = Qs
ps = pd (1 + s)
con s espresso in percentuale.
Quello che cambia rispetto alle tasse è il calcolo del surplus. Vediamo un
esempio.
Esempio
Riprendiamo le stesse funzioni di domanda e o¤erta viste in precesenza ma
ipotizziamo ora un sussidio pari a 30.
qd = 300 2pd
qs = ps 60
Il sistema è:
300 2pd = ps 60
ps = pd + 30
Da cui si ottiene:
ps = 140
pd = 110
q = 80
Vediamo i surplus:
7
P
150
s
140
120
surplus consumatore
E
110
60
d
60
80
Q
Gra…co 5
Si noti innanzitutto che stavolta è il prezzo di o¤erta a stare sopra quello di
domanda.
Il surplus del consumatore è dato dall’area delimitata in blu nel gra…co 5.
Si noti che è sempre l’area che congiunge la curva di domanda e il prezzo di
domanda, solo che stavolta questo è più in basso del prezzo di o¤erta, e l’area
non è più all’interno delle due curve, ma "esce fuori" di un triangolo. Si ha :
Sc = (150
110)(80)=2 = 1600
Il surplus del venditore è invece dato dall’area delimitata in blu nel successivo
gra…co 6, ovvero l’area che si forma tra la curva di o¤erta e il prezzo di o¤erta,
e cioè:
Sv = (140
60)(80)=2 = 3200
8
P
150
s
surplus venditore
140
120
E
110
60
d
60
Q
80
Gra…co 6
Il sussidio totale è dato dal rettangolo formato dal prezzo di o¤erta (140),
prezzo di domanda (110) e quantità di equilibrio (80), evidenziata in verde nel
gra…co 7. Cioè:
ST OT = (140
110) 80 = 2400
Il guadagno di surplus del consumatore e del venditore si calcolano per differenza e, gra…camente, sono dati dalle aree trapezoidali delimitate dal prezzo
di equilibrio senza tassa, la curva di o¤erta (o di domanda) e il prezzo di o¤erta
(o di domanda), ovvero le due aree interne al rettangolo verde delimitati dalle
linee arancioni nel gra…co 7. Si ricordi che i surplus iniziali, calcolati all’inizio
dell’esercizio, erano pari rispettivamente a 900 e 1800.
SC = 1600
900 = 700
SV = 3200
1800 = 1400
In…ne, ancora per di¤erenza, si calcola la perdita netta di benessere, data dal
triangolo delimitato esternamente dal punto di equilibrio e le curve di domanda
e o¤erta. Si tratta di calcolare la di¤erenza tra il costo totale del sussidio e il
guadagno di surplus del consumatore e del venditore.
9
PT OT = ST OT
SC
SV = 2400
P
150
700
1400 = 300
s
guadagno surplus venditore
140
120
perdita netta di benessere
E
110
guadagno surplus consumatore
60
d
60
80
Q
Gra…co 7
___________________________________________________
Letture consigliate: Hal R. Varian, Microeconomia, Libreria Editrice Cafoscarina, Cap.16
10