Modelli con varabili binarie (o qualitative)
E (Yi | X i ) = α + βX i + ε i
quando Y è una variabile benoulliana
⎧1
Y =⎨
⎩0
si ha il modello lineare di probabilità
Pr(Yi = 1 | X i ) = α + βX i + ε i
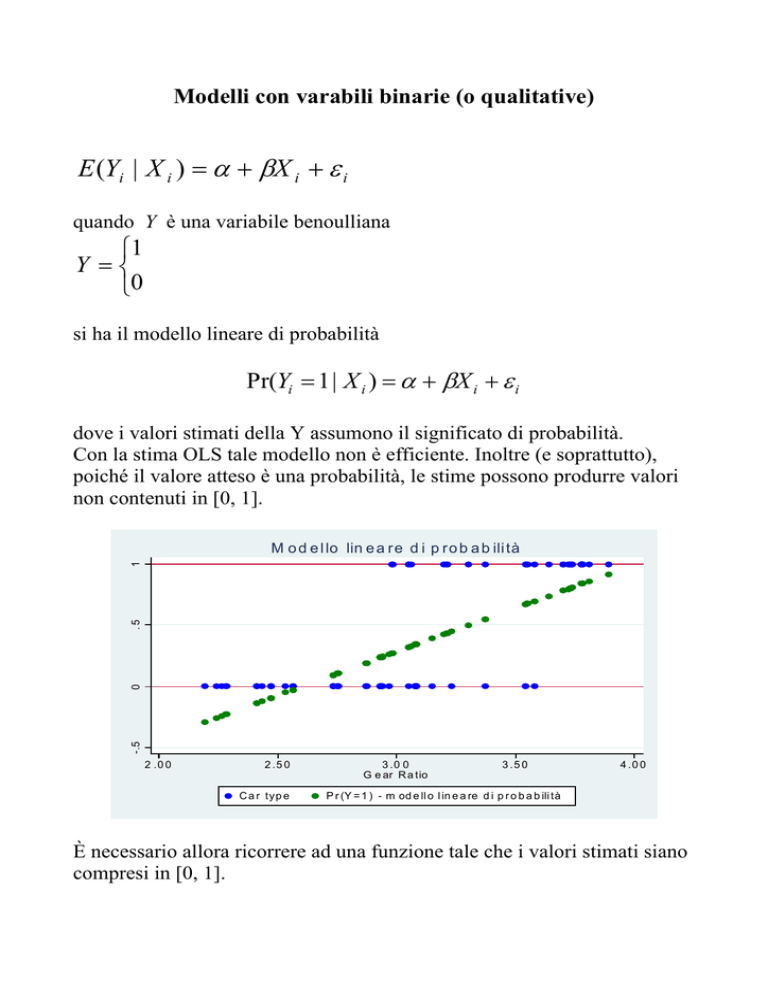
dove i valori stimati della Y assumono il significato di probabilità.
Con la stima OLS tale modello non è efficiente. Inoltre (e soprattutto),
poiché il valore atteso è una probabilità, le stime possono produrre valori
non contenuti in [0, 1].
-.5
0
.5
1
M o d e l lo lin e a re d i p ro b a b ili tà
2 .0 0
2 .5 0
C a r typ e
3 .0 0
G e ar R a tio
3 .5 0
4 .0 0
P r (Y = 1 ) - m od e ll o l in e a re d i p r o b a b ili tà
È necessario allora ricorrere ad una funzione tale che i valori stimati siano
compresi in [0, 1].
I modelli che usano tali funzioni sono noti come Logit e Probit, dove le
probabilità non sono più funzioni lineari delle caratteristiche. Il primo si
riferisce alla funzione logistica:
exp(βX i )
1
=
1 + exp(βX i ) 1 + e − βX
0
.2
P (Y =1|X )
.4
.6
.8
1
Pr(Yi = 1 | X i ) =
0
20
60
40
In d e p en d e n t va ria b le
80
100
Il Logit usa il rapporto tra le probabilità complementari della funzione
logistica detto odd:
Pr(Y = 1 | X )
P( y | x)
=
Pr(Y = 0 | X ) 1 − P( y | x)
=
exp(βX i )
exp(βX i )
1−
1 + exp(βX i )
1 + exp(βX i )
= exp( βX i ) .
Si chiama logit il logaritmo dell'odd:
⎛ P( xi ) ⎞
⎟⎟ = βX i + ε i
Logit ( Pi ) = log⎜⎜
⎝ 1 − P( xi ) ⎠
-.5
0
.5
1
M od ello lo git
2.50
2 .00
3.50
3.0 0
G ear Ratio
Pr(foreign)
Fitted values
4.00
Car type
Il modello Probit invece usa la funzione di ripartizione della normale
stand.:
1
Pr(Yi = 1 | X i ) = F ( Z i ) =
2π
cioè
Pr(Yi = 1 | X i ) = F (α + βX i + ε i ) .
∫
z
−∞
exp(− ε 2 2)dε
Entrambi le funzioni producono stime nell'intervallo [0, 1] con qualche
piccola differenza che dipende dalla distribuzione di ε, che nel caso del
probit ε ≅ N (0,1) e nel caso logit ε è una distribuzione log. stand. con
media 0 e var. = π²/3.
Metodi di stima
Bisogna stimare le probabilità di una variabile bernoulliana, la cui
distribuzione è:
f ( yi | xi , β ) = P ( xi ) yi [1 − P ( xi )]1− yi
dove P( xi ) = Pr(Yi = 1 | X i )
con osservazioni indipendenti. Allora la sua funzione di verosimiglianza è:
L( β | y ) =
∏
i
f ( yi | xi ) =
∏
i
P( xi ) yi [1 − P( xi )]1− yi .
Bisogna massimizzare questa funzione:
⎧
max : ⎨
⎩
∏
i
⎫
P( xi ) yi [1 − P ( xi )]1− yi ⎬
⎭
è più comodo però massimizzare il logaritmo della funzione di
verosimiglianza:
Log ( L( β | y )) = ∑ yi ln[ P ( xi )] + (1 − yi ) ln[1 − P( xi )]
i
Nel caso di Y=1 si ha:
Log ( L( β | y )) = ∑ y i ln[ P( xi )] = − ln[1 + exp(− βX )]
i
mentre con Y=0 si ha:
Log ( L( β | y )) = ∑ (1 − yi ) ln[1 − P( xi )] = ln(− βX ) − ln[1 + exp(− βX )]
i
Dopo la stima dei parametri del modello logit
⎛ P( xi ) ⎞
⎟ = βX i + ε i
log⎜⎜
⎟
⎝ 1 − P( xi ) ⎠
si ottengono le probabilità di Y=1|X con
exp(βX i )
1
=
1 + exp(βX i ) 1 + e− βX
mentre per la significatività delle stime dei parametri si ricorre al test Wald
che con Ho:β=0 è W~>N(0,1).
Per la verifica del modello stimato il test più usato è il rapporto di
Pr(Yi = 1 | X i ) =
verosimiglianza (LogLikelihood Ratio) LR ~ χ², una statistica che si
distribuisce come una Chi-quadro: si accetta il modello stimato se LR è
molto elevato e il suo P-value è molto piccolo, considerando i relativi
gradi di libertà.
Interpretazione delle stime di β.
P( xi )
= e βX +ε
Dato l’odds 1 − P( xi )
la relazione tra variabile dipendente e
variabile esplicativa è non-lineare. Calcolando exp(β) otteniamo la misura
dell’incremento della probabilità P(Y=1|X) all’aumento unitario della X .
P( y = 1)
Nei risultati delle stime altra cosa da considerare sono gli odds 1 − P( y = 1) e
gli odds ratio (appross. rischio relativo).
Consideriamo il caso (esempio 1) in cui la variabile binaria sia la scelta di
proseguire, come lavoro, nell’attività di ricerca e il regressore è il sesso (F
o M). Prima di tutto vediamo che il modello con la sola intercetta è
ln(odds) = -.379 e l’odds è 0.68449, cioè 128/187 in cui 128 soggetti
decidono di far ricerca. Se si decide poi di mettere il regressore nel
modello si nota che LR=25.65, significa che il modello con il regressore è
migliore. L’equazione stimata è ln(ODDS) = −.847 + 1.217Gender . A questo
punto possiamo ora prevedere le possibilità con cui i soggetti scelgono la
ricerca. Dato che l’odds è ODDS = e a +bX , nel nostro esempio se siamo di
fronte a una donna (gender=0) allora ODDS = e −.847 + 1.217 ( 0 ) = e −.847 = 0.429 ,
mentre per gli uomini si ha (gender=1) ODDS= e−.847+1.217(1) = e.37 = 1.448 , e
significa che i maschi hanno 1.448 volte possibilità in più di decidere di
fare ricerca. Trasformando questi in probabilità, cioè
ODDS
0.429
Yˆ =
=
= 0.30 , il 30% delle donne decide di far ricerca e
1 + ODDS 1.429
1.448
ODDS
=
= 0.59 , il 59% degli uomini decide di far ricerca.
Yˆ =
1 + ODDS 2.448
= 3.376 , si conclude che
Se poi si guarda l’odds ratio, cioè exp(β) e
le possibilità di far ricerca per i maschi sono 3.376 volte più alte rispetto
alle femmine, cioè 1.448/0.429=3.376.
1.217
Esempio 1:
use logistic.dta, clear
. tab decision
decision |
Freq.
Percent
Cum.
------------+----------------------------------stop |
187
59.37
59.37
continue |
128
40.63
100.00
------------+----------------------------------Total |
315
100.00
. tabodds
decision
------------------------------------------------------------cases
controls
odds
[95% Conf. Interval]
------------------------------------------------------------128
187
0.68449
0.54666
0.85707
------------------------------------------------------------logit decision
Iteration 0:
log likelihood =
-212.7832
Logistic regression
Log likelihood =
Number of obs
LR chi2(0)
Prob > chi2
Pseudo R2
-212.7832
=
=
=
=
315
0.00
.
0.0000
-----------------------------------------------------------------------------decision |
Coef.
Std. Err.
z
P>|z|
[95% Conf. Interval]
-------------+---------------------------------------------------------------_cons | -.3790784
.1147175
-3.30
0.001
-.6039204
-.1542363
-----------------------------------------------------------------------------. logit decision gender
Iteration
Iteration
Iteration
Iteration
0:
1:
2:
3:
log
log
log
log
likelihood
likelihood
likelihood
likelihood
= -212.7832
=
-199.977
= -199.95659
= -199.95659
Logistic regression
Number of obs
LR chi2(1)
Prob > chi2
Pseudo R2
Log likelihood = -199.95659
=
=
=
=
315
25.65
0.0000
0.0603
-----------------------------------------------------------------------------decision |
Coef.
Std. Err.
z
P>|z|
[95% Conf. Interval]
-------------+---------------------------------------------------------------gender |
1.216658
.244524
4.98
0.000
.7373997
1.695916
_cons | -.8472979
.1543033
-5.49
0.000
-1.149727
-.5448689
-----------------------------------------------------------------------------. scalar LR=-2*(e(ll_0)-e(ll))
. dis LR
25.653204
. tabodds
decision gender
-------------------------------------------------------------------------gender |
cases
controls
odds
[95% Conf. Interval]
------------+------------------------------------------------------------female |
60
140
0.42857
0.31672
0.57992
male |
68
47
1.44681
0.99758
2.09834
-------------------------------------------------------------------------Test of homogeneity (equal odds): chi2(1) =
25.60
Pr>chi2 =
0.0000
Score test for trend of odds:
chi2(1)
Pr>chi2
=
=
25.60
0.0000
. logit decision gender, or
Iteration
Iteration
Iteration
Iteration
0:
1:
2:
3:
log
log
log
log
likelihood
likelihood
likelihood
likelihood
Logistic regression
= -212.7832
=
-199.977
= -199.95659
= -199.95659
Number of obs
LR chi2(1)
Prob > chi2
=
=
=
315
25.65
0.0000
Log likelihood = -199.95659
Pseudo R2
=
0.0603
-----------------------------------------------------------------------------decision | Odds Ratio
Std. Err.
z
P>|z|
[95% Conf. Interval]
-------------+---------------------------------------------------------------gender |
3.375887
.8254854
4.98
0.000
2.090492
5.451639
------------------------------------------------------------------------------
Esempio 2:
logit
foreign gear_ratio
Iteration
Iteration
Iteration
Iteration
Iteration
Iteration
0:
1:
2:
3:
4:
5:
log
log
log
log
log
log
likelihood
likelihood
likelihood
likelihood
likelihood
likelihood
Logistic regression
Log likelihood = -22.054175
=
=
=
=
=
=
-45.03321
-25.213871
-22.436413
-22.064761
-22.054186
-22.054175
Number of obs
LR chi2(1)
Prob > chi2
Pseudo R2
=
=
=
=
74
45.96
0.0000
0.5103
-----------------------------------------------------------------------------foreign |
Coef.
Std. Err.
z
P>|z|
[95% Conf. Interval]
-------------+---------------------------------------------------------------gear_ratio |
5.836867
1.305948
4.47
0.000
3.277256
8.396479
_cons | -19.30575
4.210793
-4.58
0.000
-27.55875
-11.05275
Logistic regression
Log likelihood = -22.054175
Number of obs
LR chi2(1)
Prob > chi2
Pseudo R2
=
=
=
=
74
45.96
0.0000
0.5103
-----------------------------------------------------------------------------foreign | Odds Ratio
Std. Err.
z
P>|z|
[95% Conf. Interval]
-------------+---------------------------------------------------------------gear_ratio |
342.704
447.5537
4.47
0.000
26.50295
4431.434
------------------------------------------------------------------------------












