X - Didattica

Statistica per le ricerche di
mercato
A.A. 2011/12
Prof.ssa Tiziana Laureti
Dott. Luca Secondi
16. Il modello di regressione
logistica: definizione, specificazione e
stima
L’analisi delle variabili dipendenti dicotomiche
Un’importante area di applicazione dell’analisi di regressione riguarda il
caso in cui la variabile dipendente è una variabile di tipo qualitativo,
qualitativo
ossia dicotomica, nominale o ordinale.
Nelle scienze sociali le variabili dipendenti di questo tipo sono molto diffuse
in quanto rappresentano in modo appropriato numerosi fenomeni di
interesse, ad es. i giovani che conseguono il diploma decidono se iscriversi
o meno all’università, appartenenza alla forza lavoro (occupazione
/disoccupazione)
Nell’ambito delle analisi di mercato la regressione si può considerare ad
esempio la variabile dicotomica che esprime l’acquisto o non acquisto di un
prodotto in risposta ad esempio ad una diminuzione del prezzo del prodotto
oppure l’aumento della comunicazione pubblicitaria per una certa gamma di
prodotti.
Altri esempi:
•scelta tra marche (A,B)
•Possesso di un telefono cellulare
2
L’analisi delle variabili dipendenti dicotomiche
L’obiettivo è quello di spiegare la variabile risposta sulla base di uno o più
regressori.
Supponiamo di voler studiare le determinanti dell’aver o meno acquistato un
determinato modello di smartphone nell’ultimo anno. Disponiamo di
osservazioni su n individui riferite all’acquisto di uno smartphone e a k
variabili esplicative x .
Problema: utilizzando le variabili considerate (ad es. il reddito, il sesso, età,
ecc.) possiamo spiegare la scelta di acquistare o meno uno smartphone?
La nostra variabile risposta è una variabile binaria che indichiamo con Y tale
che per ogni osservazione i (i=1,…,n):
yi = 1
l'unità i-esima ha acquistato uno smartphone
yi = 0 l'unità i-esima non ha acquistato uno smartphone
L’analisi delle variabili dipendenti dicotomiche
La variabile Y si distribuisce come una v.c. di Bernoulli con parametro
P (Y = 1| X = x ) = π ( x )
π ( x)
:
P (Y = 0 | X = x ) = 1 − π ( x )
E (Y x ) = 1⋅ P (Y = 1| X = x ) + 0 ⋅ P (Y = 0 | X = x ) = π ( x )
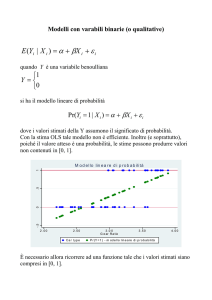
Allo scopo di modellare π ( x ) si potrebbe pensare di ricorrere ad uno
schema di regressione lineare (comunemente denominato modello di
probabilità lineare, MPL), come segue:
π ( x) = P (Y = 1| X = x ) = α + β x + ε
Il modello
lineare non
funziona!
Problema:
• dal momento che π(x) è una probabilità deve necessariamente assumere valori
nell’intervallo [0,1], mentre la funzione lineare al membro di destra può assumere
valori nell’intervallo (-∞, +∞).
• violazione dell’ipotesi di omoschedasticità
• Violazione dell’ipotesi di normalità dell’errore ε
L’analisi delle variabili dipendenti dicotomiche
Al fine di superare i problemi evidenziati in precedenza, sono stati proposti
modelli in cui si esprime la probabilità di “successo” in funzione delle
variabili esplicative, secondo una funzione G che assuma valori in [0,1]
Si parla di modelli lineari generalizzati. Uno dei più noti modelli all’interno di
tale classe è il modello di regressione logistica.
π ( x ) = P (Y = 1| X = x ) = G ( β1 X 1i + β 2 X 2i ...β k X ki )
La scelta di G cade in modo naturale sulla Funzione di ripartizione
•FdR Φ della normale standardizzata si ha il modello probit
•FdR L di una distribuzione Logistica standardizzata si ha il
modello logit (regressione logistica)
La distribuzione Logistica è simile alla Normale, con code più pesanti.
Scelta tra i due modelli:
· i risultati di solito sono indistinguibili (piccole differenze per probabilità estreme)
· il modello logit è interpretabile in termini di odds
· è difficile giustificare la scelta dell’uno o dell’altro sulla base di considerazioni teoriche
Noi studieremo il modello logit o regressione logistica
Assunzioni e specificazione del modello
1/3
Quindi nel modello di regressione logistica la probabilità π(x) è assunta
pari al valore della funzione di ripartizione di una variabile casuale logistica
calcolata in corrispondenza di x. Nel caso di una sola variabile esplicativa si
ha:
eα + β x
π ( x) = P (Y = 1| X = x ) =
+ε
α +β x
1+ e
La funzione di ripartizione logistica è
una funzione crescente di X che
assume valori nell’intervallo [0,1] e
assume la seguente forma
7
Assunzioni e specificazione del modello
2/3
Il modello logistico può essere generalizzato al caso di più variabili esplicative
come nella seguente espressione:
e β1x1 + β2 x2 +...+ βk xk
π (x) = P (Y = 1| X 2 = x2 ,..., X k = xk , ) =
β1x1 + β 2 x2 +...+ β k xk + ε
1+ e
dove - in analogia con la notazione usata nel libro di testo per il modello di
regressione lineare multipla - la variabile X1 assume valore 1
Sia nel caso univariato che in quello multivariato la funzione che lega la
probabilità di successo alle sue variabili esplicative è non lineare nei
parametri.
Essa può tuttavia essere linearizzata attraverso un’opportuna
trasformazione.
8
Assunzioni e specificazione del modello
3/3
Dal momento che la probabilità di successo π ( x) è data dalla formulazione
appena introdotta, la probabilità di insuccesso (complementare) è pari a:
1 − π ( x) = P (Y = 0 | X 2 = x2 ,..., X p = x p , ) =
1
1 + e β1x1 + β2 x2 +...+ βk xk
Il rapporto tra le due probabilità è quindi dato da:
π ( x)
= e β x + β x +...+ β x
1 − π ( x)
1 1
2 2
k k
passando al logaritmo naturale per ambo i membri si ottiene la seguente
trasformazione - detta logit – che produce una funzione lineare nei parametri
β1,…, βk
⎛ π ( x) ⎞
logit [π (x) ] = log ⎜
= β1 x1 + β 2 x2 + ... + β k xk
⎟
⎝ 1 − π ( x) ⎠
Nei processi di stima anziché considerare il valore di π(x) si opera attraverso
la sua trasformata logit.
9
Logit e odds
L’ODDS è il rapporto tra la probabilità di successo e quella di insuccesso
successo e insuccesso sono equiprobabili
⎧ 1
π ( x)
⎪
= ⎨∈ ( 0,1) il successo è meno probabile dell'insuccesso
ODDS =
1 − π ( x) ⎪
⎩ ∈ (1, ∞ ) il successo è più probabile dell'insuccesso
L'odds corrisponde al rapporto fra il numero di volte in cui l'evento si
verifica (o si è verificato) ed il numero di volte in cui l'evento non si
verifica (o non si è verificato)
Poiché il campo di variazione dell’odds non è simmetrico, spesso si preferisce
ricorrere alla sua trasf. logaritmica, il LOG ODDS, che risulta uguale alla trasformata
logit di π .
successo e insuccesso sono equiprobabili
⎧0
⎡ π ( x) ⎤
⎪
π
log(ODDS ) = log ⎢
logit
(
)
=
x
=
[
]
⎨<0 il successo è meno probabile dell'insuccesso
⎥
⎣1 − π ( x) ⎦
⎪ >0 il successo è più probabile dell'insuccesso
⎩
10
Esempio di odds
Gli odds si utilizzano nel mondo delle scommesse perché consentono allo
scommettitore di calcolare facilmente la somma da incassare in caso di
vittoria.
Per esempio si ipotizzi che le probabilità di vittoria per una squadra di calcio
al campionato italiano siano date dai bookmakers 4:1 “a sfavore”.
Questo equivale a dire che le probabilità di sconfitta (π) della squadra sono
state considerate 4 volte più alte di quelle di una sua vittoria pari a (1-π).
Quindi la vittoria della squadra è da pagare 4 volte la cifra scommessa
Gli odds si possono trasformare in probabilità: la squadra considerata ha 1
probabilità su 5 (p = 0,2) di vincere e 4 probabilità su 5 di perdere (1-p = 0,8)
11
Interpretazione dei parametri del modello
‰Si può dimostrare che il generico parametro βj è il risultato della variazione
prodotta sul logit[π(x)] dall’incremento unitario della variabile indipendente Xj
(tenuti costanti i valori degli altri regressori). Quindi il segno del coefficiente
di regressione della variabile Xj corrisponde al segno dell’effetto da essa
esercitato.
‰ Per avere una misura dell’intensità si utilizza l’odds ratio (OR) dato dal
rapporto degli odds
OR( j )
odds ⎡⎣π (x) | X jB ⎤⎦
β x +...+ β x +...+ β x
β x
j jB
k k
e 11
e j jB
β ( x −x )
β
=
= β1x1 +...+ β j x jA +...+ βk xk = β j x jA = e j jB jA = e j
odds ⎡⎣π (x) | X jA ⎤⎦ e
e
Dalla espressione riportata sopra, si deduce pertanto che per variazioni
della generica variabile indipendente Xj la misura odds ratio è pari
all’esponenziale del corrispondente parametro.
12
Interpretazione dei parametri del modello
1. Se non sussiste nessuna relazione tra la variabile esplicativa Xj e la
probabilità che la variabile risposta Y assuma valore 1 il valore dell’odds
ratio è pari a 1 da cui βj = 0
2. Valori dell’odds ratio maggiori di 1 - ai quali corrispondono valori del
parametro βj maggiori di 0 - indicano un effetto positivo della variabile
esplicativa Xj sulla probabilità che la variabile risposta Y assuma il valore 1.
3. Valori dell’odds ratio compresi tra 0 e 1 - ai quali corrispondono valori del
parametro βj minori di 0 - indicano un effetto negativo della variabile
esplicativa Xj sulla probabilità che la variabile risposta Y assuma il valore
1.
NB. L’esistenza di tale asimmetria (nei valori degli odds ratio) richiede cautela
quando si confrontano odds ratio caratterizzati da segno diverso. Ad
esempio, un OR positivo pari a 2 ha esattamente la stessa intensità di un
OR “negativo” pari a 1/2=0,5
13
Cenni alle procedure di stima dei parametri
La stima del vettore dei parametri ignoti β è effettuata con il metodo della
massima verosimiglianza, che si basa sulla massimizzazione della probabilità
di osservare l’insieme dei dati relativi al campione estratto in funzione di β.
In termini estremamente semplici, si può affermare che la funzione di
verosimiglianza, rappresenta la probabilità di osservare prima
dell’esperimento, quel particolare campione che si è verificato.
Data l’indipendenza delle osservazioni, la verosimiglianza del campione di n
unità - indicata con il simbolo L(β) - è data dal prodotto delle verosimiglianze
relative alle unità che lo compongono e - una volta estratto il campione - è
funzione dei soli parametri β, come nell’espressione seguente:
n
L(β) = ∏ f ( yi | xi ; β)
i =1
Per ottenere la stima di massima verosimiglianza dei parametri, si determina il valore β che
massimizza L(β) (o verosimilmente il suo logaritmo considerata la monotonicità della funzione
logaritimica), ossia quel valore di β per cui il campione osservato è più plausibile.
Ponendo uguali a 0 le derivate parziali fatte rispetto ai k parametri da stimare si ottengono le
equazioni di verosimiglianza che - in quanto non lineari nei parametri - richiedono l’applicazione di
metodi iterativi (implementati nei più comuni pacchetti informatico-statistici).
14
Esempio di stima di odds ratio
Si ipotizzi di effettuare un’analisi di regressione logistica che modelli la
probabilità di progresso nella conoscenza dell’inglese (Y=1 Î progresso)
in funzione dell’esposizione ad un nuovo metodo di studio (X =1 Î
esposizione) ottenendo una stima del relativo parametro β pari a 2.
Tale risultato indica un effetto positivo dell’esposizione al nuovo metodo
sull’apprendimento della lingua straniera, che si traduce in una maggiore
probabilità di osservare un progresso nella conoscenza della lingua in caso
di esposizione al nuovo metodo.
Tale maggiore probabilità può essere meglio quantificata tramite la stima
dell’odds ratio corrispondente al passaggio dallo stato 0 allo stato 1 della
variabile X , data da exp(β) = exp(2) = 7,4
Dalla stima dell’OR si deduce che la frequenza relativa di coloro che hanno
progredito nella conoscenza della lingua è oltre 7 volte superiore nel
gruppo degli esposti al nuovo metodo rispetto al gruppo dei non esposti.
15
Inferenza nel modello di regressione logistica
Bontà del modello nel suo complesso
(1/4)
Per verificare la significatività di un modello nel suo complesso si calcola la differenza G - detta
extradevianza - tra la devianza del modello avente la sola intercetta e la devianza del modello in
esame, basata sul rapporto di verosimiglianza, secondo la seguente espressione
G = D(modello intercetta) − D (modello completo) = −2log
L(0)
L (β )
dove L(0) rappresenta la massima verosimiglianza in corrispondenza del modello con la
sola intercetta, mentre L(β) rappresenta la massima verosimiglianza in corrispondenza
del modello completo.
La verifica della bontà di un modello sulla base del rapporto di verosimiglianza (Likelihood Ratio,
LR) si fonda sull’idea che se le variabili considerate aggiungono molta informazione al modello con
la sola intercetta, la verosimiglianza relativa al modello completo L(β) sarà molto maggiore di quella
che si ottiene considerando il modello con la sola intercetta L(0). In tal caso il rapporto di
verosimiglianza tende ad assumere valori molto piccoli, anche prossimi allo zero.
16
Inferenza nel modello di regressione logistica
Bontà del modello nel suo complesso
(2/4)
Attraverso la statistica G, basata sul rapporto di verosimiglianza, si sottopone a verifica
il seguente sistema di ipotesi:
H0:
H1:
β2 = … = βk = 0
almeno un βj ≠ 0 dove j=2,…,k
Si può dimostrare che sotto ipotesi nulla G si distribuisce come una χ2 con k-1 gradi di libertà.
Pertanto si respinge l’ipotesi nulla se si verifica che:
G>χ
2
k −1,α 2
È desiderabile che il valore di G sia elevato
Î le variabili esplicative introducono una
quantità significativa di informazione rispetto
alla sola intercetta
17
Inferenza nel modello di regressione logistica
Bontà del modello nel suo complesso
(3/4)
Per la valutazione della bontà di adattamento del modello di regressione
logistica ai dati si può ricorrere ad una misura analoga al coefficiente di
determinazione multiplo.
multiplo Cox and Snell (1989) hanno proposto la seguente
generalizzazione del coefficiente di determinazione per modelli non lineari
chiamato Pseudo-R2
⎡ L(0) ⎤
R = 1− ⎢
⎥
L
(
β
)
⎣
⎦
2
g
2
n
dove L(0) e L(β) rappresentano rispettivamente la massima verosimiglianza in
corrispondenza del modello con la sola intercetta e la massima verosimiglianza in
corrispondenza del modello considerato, dove n è la numerosità delle osservazioni.
Il coefficiente di determinazione può variare tra 0, corrispondente alla situazione in cui il
modello considerato non aggiunge informazione al modello con la sola intercetta per cui
2n
vale L(β) = L(0) - e il suo valore massimo, che è: R2
= 1 − L(0)
g ,MAX
[
]
18
Inferenza nel modello di regressione logistica
Bontà del modello nel suo complesso
(4/4)
Poiché R2g,max è minore di 1, per poter disporre di una misura che
varia tra 0 e 1, dove zero rappresenta assenza di adattamento
e 1 adattamento massimo del modello ai dati (come già visto
per il modello di regressione lineare), si può far riferimento al
coefficiente riscalato (Nagelkerke, 19991):
2
g
R =
2
g
R
2
g , MAX
R
19
Inferenza nel modello di regressione logistica
Confronto tra due modelli comparabili
Una procedura analoga può essere utilizzata per confrontare i modelli annidati:
modello completo Î k-1 variabili esplicative
modello ridotto Î le ultime s variabili del modello completo sono escluse (totale
variabili: k-s-1).
Il sistema di ipotesi è pertanto il seguente:
H 0:
H 1:
βk-s+1 = βk-s+2 = … = βk = 0
almeno un’uguaglianza in H0 non è vera
Si calcola quindi l’extradevianza Gs che misura la differenza tra la devianza del
modello ridotto e quella del modello completo
Si può dimostrare che sotto ipotesi nulla Gs si distribuisce come una χ2 con s
gradi di libertà; pertanto si respinge l’ipotesi nulla se si verifica che:
Gs > χ
2
s ,α 2
20
Inferenza nel modello di regressione logistica
Significatività per ogni singolo parametro
Per verificare la significatività della stima bj del j-esimo parametro del modello
si fa ricorso generalmente al test di Wald, nel caso univariato dato da
bj
W=
s (b j )
Talvolta i pacchetti statistici, anziché
fornire la statistica W forniscono il suo
quadrato (Wald Chi-Square), che si
distribuisce come una χ2 con un grado
di libertà
stima
Errore standard
Sulla base dell’ipotesi nulla del seguente sistema di ipotesi:
H0: βj = 0
H1: βj ≠ 0
W si distribuisce come una distribuzione normale standardizzata
Se nell’effettuazione del test si verifica che W > zα
2
si respinge l’ipotesi nulla e si conclude che il parametro è significativamente
diverso da 0 Î la variabile esplicativa corrispondente influisce sulla variabile
risposta.
21
Stime di modelli di regressione logistica
1/7
Una ricerca di mercato si propone di stimare la probabilità di acquisto di un particolare snack
alimentare sulla base di un insieme di variabili esplicative raccolte attraverso un’indagine
campionaria che ha coinvolto 32 giovani di età compresa tra i 12 e i 29 anni.
La ricerca ha rilevato, insieme ad altre variabili di seguito illustrate, l’acquisto da parte del
rispondente di almeno una snack nel corso dell’ultimo mese. Nella codifica di tale variabile è
stato attribuito valore 1 nel caso in cui il rispondente ha dichiarato di avere acquistato almeno
uno snack nel corso dell’ultimo mese e 0 altrimenti. Questa variabile rappresenta la variabile
risposta del modello di regressione logistica che si intende stimare.
Le altre variabili rilevate sono le seguenti:
•
Numero medio mensile di snack consumati (n_pezzi_medio) calcolato sulla base
degli acquisti effettuati negli ultimi 6 mesi;
•
Età del rispondente;
•
Esposizione alla pubblicità relativa al prodotto in questione (tale variabile, di tipo
dummy, assume valore 1 nel caso in cui il rispondente dichiari di aver visto almeno
una volta alla televisione lo spot pubblicitario del prodotto in questione; 0 altrimenti);
22
Stime di modelli di regressione logistica
2/7
Dataset in Stata
(prime 20 unità)
23
Stime di modelli di regressione logistica
Iteration
Iteration
Iteration
Iteration
Iteration
Iteration
0:
1:
2:
3:
4:
5:
log
log
log
log
log
log
likelihood
likelihood
likelihood
likelihood
likelihood
likelihood
=
=
=
=
=
=
-20.59173
-13.496795
-12.929188
-12.889941
-12.889633
-12.889633
Logistic regression
Number of obs
LR chi2( 3)
Prob > chi2
Pseudo R2
Log likelihood = -12.889633
acquisto
Coef.
n_pezzi_me~o
etax
espos_pubb
_cons
2.826113
.0951577
2.378688
-13.02135
. logit
3/7
Std. Err.
z
1.262941
.1415542
1.064564
4.931325
2.24
0.67
2.23
-2.64
P>|z|
0.025
0.501
0.025
0.008
=
=
=
=
32
15.40
0.0015
0.3740
[95% Conf. Interval]
.3507938
-.1822835
.29218
-22.68657
5.301432
.3725988
4.465195
-3.35613
Iteration
Iteration
Iteration
Iteration
Iteration
Iteration
acquisto n_pezzi_medio etax espos_pubb,or
0:
1:
2:
3:
4:
5:
log
log
log
log
log
log
likelihood
likelihood
likelihood
likelihood
likelihood
likelihood
=
=
=
=
=
=
-20.59173
-13.496795
-12.929188
-12.889941
-12.889633
-12.889633
Logistic regression
Number of obs
LR chi2(3)
Prob > chi2
Pseudo R2
Log likelihood = -12.889633
acquisto
Odds Ratio
n_pezzi_me~o
etax
espos_pubb
16.87972
1.099832
10.79073
Std. Err.
z
21.31809
.1556859
11.48743
2.24
0.67
2.23
P>|z|
0.025
0.501
0.025
=
=
=
=
32
15.40
0.0015
0.3740
[95% Conf. Interval]
1.420194
.8333651
1.339344
200.6239
1.451502
86.93802
24
Stime di modelli di regressione logistica
4/7
Dopo aver stimato il modello in Stata, è possibile calcolare per ogni osservazione
campionaria “la probabilità prevista” di avere un successo (corrispondente in questo
specifico caso, alla probabilità di acquistare lo snack), dati i valori assunti dalle variabili
indipendenti (la nuova variabile generata è chiamata pr_for). Come per ogni altra
variabile nel dataset, è possibile ottenere alcune misure di sintesi attraverso il comando
summarize.
. sum pr_for
Variable
Obs
Mean
Std. Dev.
pr_for
32
.34375
.3169032
Min
.0244704
Max
.9453403
E’ possibile allo stesso tempo (attraverso il comando prvalue) computare, sempre sulla
base della relazione stimata, la probabilità di avere un successo e quindi la
P(Y=1|x) quando le variabili indipendenti xi assumono particolari e specifici valori.
logit: Predictions for acquisto
Confidence intervals by delta method
Pr(y=1|x):
Pr(y=0|x):
x=
n_pezzi_me~o
3.1171875
0.1068
0.8932
etax
21.9375
95% Conf. Interval
[-0.0502,
0.2637]
[ 0.7363,
1.0502]
Probabilità di acquistare il
prodotto per un individuo
che non ha visto lo spot
pubblicitario
espos_pubb
0
25
Stime di modelli di regressione logistica
. prvalue, x (espos_pubb=1) rest(mean)
logit: Predictions for acquisto
Confidence intervals by delta method
Pr(y=1|x):
Pr(y=0|x):
x=
n_pezzi_me~o
3.1171875
0.5633
0.4367
etax
21.9375
5/7
Probabilità di acquistare il
prodotto per un individuo
che ha visto lo spot
pubblicitario
95% Conf. Interval
[ 0.2432,
0.8833]
[ 0.1167,
0.7568]
espos_pubb
1
26
Stime di modelli di regressione logistica
6/7
Riprendiamo l’esempio introdotto in aula informatica…
. xi: logit acq_ol redd eta sesso n_fam conness antivir i.istruz
i.istruz
_Iistruz_1-3
(naturally coded; _Iistruz_1 omitted)
Iteration
Iteration
Iteration
Iteration
Iteration
Iteration
0:
1:
2:
3:
4:
5:
log
log
log
log
log
log
likelihood
likelihood
likelihood
likelihood
likelihood
likelihood
=
=
=
=
=
=
Stima di un modello
Logit in Stata
-68.59298
-46.620777
-44.162084
-43.919393
-43.91555
-43.915549
Logistic regression
Number of obs
LR chi2(8)
Prob > chi2
Pseudo R2
Log likelihood = -43.915549
acq_ol
Coef.
redd
eta
sesso
n_fam
conness
antivir
_Iistruz_2
_Iistruz_3
_cons
.0001806
-.0959763
-.1888113
-.1618627
1.265137
.5097538
1.585548
1.781341
1.824165
Std. Err.
.0004077
.0250225
.5454956
.2778335
.642813
.5409597
.847488
.8269445
1.812384
z
0.44
-3.84
-0.35
-0.58
1.97
0.94
1.87
2.15
1.01
P>|z|
0.658
0.000
0.729
0.560
0.049
0.346
0.061
0.031
0.314
=
=
=
=
100
49.35
0.0000
0.3598
[95% Conf. Interval]
-.0006186
-.1450196
-1.257963
-.7064063
.0052466
-.5505076
-.0754981
.1605596
-1.728042
.0009797
-.0469331
.8803404
.3826809
2.525027
1.570015
3.246594
3.402122
5.376371
27
Stime di modelli di regressione logistica
7/7
Riprendiamo l’esempio introdotto in aula informatica…
. xi: logit acq_ol redd eta sesso n_fam conness antivir i.istruz, or
i.istruz
_Iistruz_1-3
(naturally coded; _Iistruz_1 omitted)
Iteration
Iteration
Iteration
Iteration
Iteration
Iteration
0:
1:
2:
3:
4:
5:
log
log
log
log
log
log
likelihood
likelihood
likelihood
likelihood
likelihood
likelihood
=
=
=
=
=
=
-68.59298
-46.620777
-44.162084
-43.919393
-43.91555
-43.915549
L’output del software
restituisce gli Odds
Ratio (OR)
Logistic regression
Number of obs
LR chi2(8)
Prob > chi2
Pseudo R2
Log likelihood = -43.915549
acq_ol
Odds Ratio
redd
eta
sesso
n_fam
conness
antivir
_Iistruz_2
_Iistruz_3
1.000181
.9084855
.8279427
.850558
3.543578
1.664881
4.881965
5.937814
Std. Err.
.0004078
.0227326
.4516391
.2363135
2.277858
.9006336
4.137407
4.910242
Stima di un modello
Logit in Stata
z
0.44
-3.84
-0.35
-0.58
1.97
0.94
1.87
2.15
=
=
=
=
100
49.35
0.0000
0.3598
P>|z|
[95% Conf. Interval]
0.658
0.000
0.729
0.560
0.049
0.346
0.061
0.031
.9993816
.8650053
.2842324
.4934142
1.00526
.576657
.9272815
1.174168
1.00098
.9541513
2.411721
1.46621
12.49124
4.806722
25.70264
30.02776
28