decisioni e probabilità soggettiva

Andrea ELLERO
DECISIONI E
PROBABILITÀ SOGGETTIVA
Appunti per il corso di
METODI MATEMATICI PER L’ECONOMIA DELL’ARTE
A.A. 2005-2006
2
Queste pagine raccolgono alcune lezioni del corso di METODI
MATEMATICI PER L’ECONOMIA DELL’ARTE per la laurea specialistica in
Economia e Gestione delle Arti e delle Attività Culturali dell’Università Ca’
Foscari di Venezia (a.a. 2004-2005).
Ringrazio la Dott. Francesca Cerisano che ha fornito una prima versione
dattiloscritta degli appunti delle lezioni.
3
Elementi di teoria delle decisioni
La teoria delle decisioni è una disciplina che studia il processo logico-formale con cui un
individuo si accinge ad assumere un comportamento, a suo avviso ottimale, in presenza di
informazioni incomplete o, come si suole dire, in condizioni di incertezza.
Un individuo si trova a dover prendere delle decisioni in condizione di incertezza quando
deve scegliere una fra più azioni possibili, le cui conseguenze non sono determinabili a
priori, nel senso che ogni alternativa contemplata condurrà certamente ad una delle
conseguenze previste senza, però, poter stabilire esattamente a quale di esse.
Solitamente, si suppone che l’incertezza che lascia indeterminata la conseguenza,
dipenda dalla “non conoscenza” di alcuni eventi (o stati di natura) e che le conseguenze di
ciascuna scelta possano essere valutate in termini di utilità o di perdita.
1.
Criteri decisionali in condizioni di incertezza
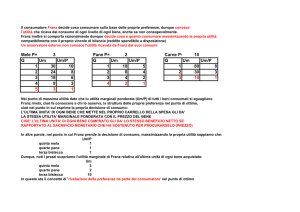
Supponiamo di dover allestire una mostra temporanea utilizzando sia spazi al coperto che
spazi al chiuso. Possiamo scegliere di sfruttare gli spazi al coperto (decisione o alternativa
d1), quelli esterni (decisione d2), oppure in eguale misura tali spazi (decisione d3). Gli spazi
al coperto comportano costi maggiori ma, ovviamente, comportano un numero di visite più
elevato in caso di cattivo tempo.
Nel periodo di fruibilità della mostra ci si attende dunque un profitto che dipende dalle
condizioni atmosferiche e dalla decisione all’utilizzo degli spazi espositivi effettuata
inizialmente. Considerati tre possibili scenari (o stati di natura) futuri s1 (tempo
prevalentemente piovoso), s2 (tempo variabile), s3 (tempo prevalentemente soleggiato)
sono stati valutati i possibili profitti come raccolti nella seguente tabella, detta matrice delle
utilità (o dei payoff):
s1
s2
s3
d1
2.29
1
3.68
d2
2
4.75
4.32
d3
0
4
2
4
Indicheremo con M ij il risultato corrispondente alla decisione i nel caso si realizzi lo
scenario j.
Una rappresentazione diversa, che consente di cogliere quale sia la sequenza di
decisioni/esiti all’interno del processo decisionale è data dal cosiddetto albero di decisione:
Come stabilire quale sia la decisione più conveniente, in termini di profitto/utilità?
Osserviamo anzitutto che l’alternativa d3 presenta utilità minori o uguali alle utilità di d2, in
corrispondenza di ciascuno scenario sj, si dice in questo caso che d3 è dominata da d2 e,
ai fini della nostra scelta, d3 è chiaramente una decisione inopportuna, da scartare.
Resta da compiere la scelta, non ovvia ed immediata, tra d1 e d2.
Vediamo una rassegna dei più noti criteri di scelta proposti dalla letteratura.
1.1 Criterio di Wald (del maximin)
Il decisore suppone che si realizzi, in corrispondenza di ciascuna alternativa, lo scenario
peggiore.
Nel nostro esempio:
s1
s2
s3
minimo
d1
2.29
1
3.68
1
d2
2
4.75
4.32
2
5
Dopo aver rilevato i valori minimi per ogni riga, scegliamo tra questi quello massimo,
max(min M ij )
minimizzando, in tal modo, la perdita:
i
j
Nel nostro esempio la scelta cade sull’alternativa d2.
1.2
Criterio dell’ottimismo
Il decisore suppone che si realizzi, in corrispondenza di ciascuna alternativa, lo scenario
migliore.
Nel nostro esempio:
s1
s2
s3
massimo
d1
2.29
1
3.68
3.68
d2
2
4.75
4.32
4.75
Dopo aver rilevato i valori massimi per ogni riga, scegliamo tra questi quello massimo,
minimizzando, in tal modo, la perdita:
min(max M ij )
i
j
Nel nostro esempio la scelta cade sull’alternativa d2.
Dunque, l’alternativa d2 è ancora la migliore.
1.3
Criterio di Laplace o della media aritmetica
Si sceglie l’alternativa che presenta media aritmetica delle utilità più elevata.
Nell’esempio le medie aritmetiche sono 2.32 per d1 e 3.69 per d2.
La scelta migliore è ancora d2 .
1.4
Criterio di Savage (minimax dei regret)
Questo criterio prevede una scelta fondata sulla valutazione, per ogni fissato stato di
natura, il mancato guadagno (regret, rammarico) che, in corrispondenza di ciascuna
decisione, si ha rispetto alla decisione migliore per quello stato di natura (la decisione che
si adotterebbe in condizioni di informazione perfetta).
Costruiamo, a partire dalla matrice dei payoff la matrice dei Regret, definendo il regret
corrispondente alla decisione i nel caso si realizzi lo stato j
rij = (max M kj ) − M ij
k
6
Tra tutte le decisioni opteremo per quella che presenta il più basso valore massimo del
min(max rij )
regret (minimax):
i
j
Nell’esempio:
[regret]
s1
s2
s3
d1
0
3.75
0.64
3.75
d2
0.29
0
0
0.29
max regret
La scelta da adottare è ancora d2.
1.5
Criterio delle eccedenze (maximin delle eccedenze)
Contrariamente al criterio precedente, si calcola, in corrispondenza di ciascuno scenario,
la distanza (eccedenza) dalla scelta che presenta il profitto minore per un fissato stato di
natura. Per questo motivo costruiamo, a partire dalla matrice delle utilità, la matrice delle
eccedenze, definendo l’eccedenza corrispondente alla decisione i nel caso si realizzi lo
stato j
eij = M ij − (min M kj )
k
La scelta cadrà sulla decisione che presenta il più alto valore minimo di eccedenza
max(min eij )
(maxmin):
i
j
Tornando all’esempio:
[eccedenze]
s1
s2
s3
d1
0.29
0
0
0
d2
0
3.75
0.64
0
min eccedenza
Le decisioni sono valutate come equivalenti.
Osservazione: non abbiamo considerato la variabilità delle utilità in corrispondenza di
una singola decisione; possiamo tuttavia osservare che l’alternativa d3 è, da questo punto
di vista, desiderabile poiché seppure non fornisca profitti molto elevati evita il rischio di
profitti molto bassi; opportuni criteri, che qui non consideriamo, consentono di tener conto
di questo importante aspetto.
7
1.6 Un altro esempio
Data la matrice delle utilità:
s1
s2
s3
d1
20
2
-6
d2
9
8
0
d3
4
4
5
determiniamo la decisione migliore con l’ausilio dei diversi criteri analizzati.
s1
s2
s3
Wald
d1
20
2
-6
-6
20
5.3
d2
9
8
0
0
9
5.7
4
4
5
4
5
4.3
d3
d1
d2
d3
ottim. Laplace
Regret :
s1
d3
s3
0
6
11
11
0
5
16
4
0
d1
d2
s2
max Regret
11
11
16
d1 e d2
Eccedenze:
s1
s2
s3
min eccedenza
d1
16
0
0
0
d2
5
6
6
5
d3
0
2
11
0
d2
8
2.
Calcolo delle Probabilità
Introduzione
La logica elementare divide gli enunciati (che qui chiameremo eventi) in veri e falsi,
ammettendo, per principio, che non vi siano altre possibilità di qualificarli (secondo il
classico principio del Terzo Escluso aristotelico, una proposizione non può che essere
vera o falsa – tertium non datur). Tuttavia se qualcuno dice: “domani pioverà”,
quest’affermazione non è né vera, né falsa in questo momento; soltanto domani, dopo che
avremo constatato le condizioni del tempo, potremo attribuirle una delle due qualifiche. In
attesa di una verifica, dunque, due persone possono avere valutazioni contraddittorie circa
la verità o falsità di un’affermazione, senza che si possa decidere quale delle due abbia
ragione, possono cioè avere un grado di fiducia diverso riguardo al verificarsi dell’evento.
Se ci è consentito scommettere sull’una o sull’altra possibilità (ed è quello che facciamo
quando decidiamo o meno di portare con noi l’ombrello quando ancora non piove) l’entità
della nostra scommessa è un indice del nostro grado di fiducia nell’enunciato e, perciò,
può prendersi come “misura” del grado di verità che siamo disposti ad attribuirgli.
2.1
La definizione di probabilità soggettiva
Diamo ora una definizione precisa di probabilità, rifacendoci alla concezione soggettiva di
de Finetti (1937).
DEFINIZIONE
La probabilità di un evento E, secondo l’opinione di un dato individuo, è il prezzo P(E) che
egli giudica “equo” pagare per riscuotere un importo unitario nel caso in cui E si verifichi.
Supponiamo di voler assegnare in modo soggettivo una probabilità all’evento
E = “Il prossimo vincitore delle elezioni USA sarà un repubblicano” .
Tale probabilità è, per definizione, il prezzo (certo) che siamo disposti a pagare oggi per
riscuotere 1€ nel caso in cui E si verifichi (in futuro!). Se siamo disposti a scommettere
0.25 €, 25 centesimi, allora la nostra valutazione di probabilità è P(E)=0.25=1/4.
9
Uno schema grafico può aiutare ad illustrare lo svolgimento temporale della scommessa:
pago certamente P(E)
riscuoto 1 se E si verifica in futuro
futuro
Oggi
Il termine “prezzo equo” nella definizione di probabilità sta ad indicare che i verbi pagare e
riscuotere devono poter essere scambiati senza che la valutazione di probabilità cambi: in
altri termini, riguardo alla scommessa sul futuro Presidente degli Stati Uniti dobbiamo
essere anche disposti ad accettare (facendo da “banco”) la scommessa che stabilisce di
pagare 1€ in futuro nel caso si realizzi l’evento E, riscuotendo 0.25 € oggi.
La probabilità da assegnarsi ad un evento che si realizzerà sicuramente (evento certo)
dovrà di conseguenza essere uguale a 1 [P(E)=1], perché, in questo caso, riscuoteremo
certamente 1 €, avendo la certezza della realizzazione di E.
La probabilità di un evento che senza dubbio non si realizzerà (evento impossibile) dovrà
invece essere uguale a 0 [P(E)=0], perché tale è la somma che siamo disposti a sborsare,
avendo la consapevolezza di scommettere sul realizzarsi di un evento che non accadrà
mai.
La probabilità deve essere allora un numero compreso tra i due valori soglia 0 e 1:
P(E) ∈ [0,1] .
Osservazione importante. Se P(E)=0, ciò non implica l’impossibilità del realizzarsi
dell’evento stesso. Vediamo un esempio.
Consideriamo un bersaglio quadrato di lato unitario e supponiamo di sparare a caso (ad
occhi chiusi) colpendo il punto di coordinate (¾,¾). Si è realizzato l’evento H = “viene
colpito il punto (¾,¾)”.
1
¾ ––––––●




0
¾
1
10
Supponiamo ora di ripetere l’esperimento: qual è la probabilità di riuscire a colpire di
nuovo il medesimo punto? Essendo infiniti i punti del piano, infinite saranno le nostre
possibilità e 0 è ciò che saremmo disposti a pagare nello scommettere sulla realizzazione
di H: l’evento è “altamente improbabile”, ma non impossibile.
2.2
Probabilità, scommesse e quote.
Ritorniamo all’evento E= “Il prossimo vincitore delle elezioni USA sarà un repubblicano”.
Su tale evento è possibile effettuare delle scommesse (nel web è facile reperire aziende
che, più in generale, gestiscono scommesse “a quota fissa”, in Italia si può vedere ad
esempio il sito della SNAI, www.snai.it). Tipicamente una società di gestione di
scommesse presenta per ogni evento sul quale si può scommettere la quota con la quale
viene ricompensata una giocata unitaria nel caso si realizzi l’evento. Naturalmente quota e
probabilità sono inversamente proporzionali ma vediamo le cose più precisamente.
Definiamo quota equa relativa all’evento E la quantità
q(E) =
1
P( E )
Dire che la quota equa è di 4 a 1, significa che all’evento viene assegnata la probabilità ¼.
Non abbiamo, però, ancora precisato il motivo per il quale parliamo di quota equa q. Infatti,
si utilizza tale aggettivo per distinguerla dalla quota reale Q. Quest’ultima risulta
comprensiva delle remunerazioni αi, per i gestori delle scommesse.
La quota reale, quella effettivamente pubblicata dal gestore (il banco) è:
Q(Ei) = (1 – αi) q(Ei)
Pertanto la valutazione di probabilità effettuata dal gestore è
P(Ei) =
1−αi
1
1
=
<
q ( Ei )
Q( Ei )
Q( Ei )
La probabilità assegnata dal gestore ad Ei è minore di
1
(1) .
Q( Ei )
(1) Per legge, il guadagno del banco viene limitato. Si parla, perciò, della cosiddetta percentuale di
n
allibramento: PA =
∑
i =1
100
Qi
. Tale percentuale deve essere inferiore alla percentuale di allibramento massima
PAmax, fissata per legge. Possiamo notare che se αi = 0
∀ i, allora: PA =
n
∑
i =1
100
= 100
q ( Ei )
∑ P(Ei) =100.
In altre parole, nel caso di tutte quote eque la percentuale di allibramento è 100. Nel caso in cui αi>0 per
almeno un indice i, si ha PA >100 ovvero, nel caso delle quote reali PA è superiore a 100.
11
2.3
Il requisito della coerenza
Consideriamo un insieme di eventi Ω = { E1, E2, E3…En } che siano incompatibili (o
esclusivi: si può realizzare soltanto uno di essi) ed esaustivi (si realizza almeno uno di
essi). Diremo in tal caso spazio campionario l’insieme Ω e chiameremo eventi elementari i
suoi elementi.
Ω
area = P(E1)
Assegnando una probabilità ad ogni evento, si ottiene una funzione:
P : Ω → [ 0, 1] ;
Ei → P(Ei)
che ad ogni evento Ei associa la corrispondente valutazione di probabilità P(Ei).
Poiché gli eventi sono esaustivi la probabilità che non si realizzi alcun evento di Ω (Evento
impossibile = Ø) è P(Ø) = 0, mentre la probabilità che si realizzi almeno un evento di Ω
ovvero che si realizzi Ω (evento certo) è P(Ω) = 1.
Vediamo ora come valutare le probabilità degli eventi dell’insieme delle parti P (Ω) dello
spazio campionario Ω (l’insieme delle parti è un insieme che ha per elementi tutti i
sottoinsiemi di Ω, compresi l’insieme vuoto Ø
e l’insieme Ω stesso). A partire dalle
probabilità assegnate agli eventi elementari possiamo estendere la valutazione ad altri
sottoinsiemi di Ω. Vogliamo però che tale estensione sia coerente nel senso che andiamo
a definire.
DEFINIZIONE
Una valutazione di probabilità è detta coerente se nessuna combinazione di scommesse
consente di realizzare un guadagno certo (assenza di arbitraggi).
12
Lavoreremo d’ora in poi solo con valutazioni di probabilità coerenti.
Teorema La richiesta di coerenza è equivalente a chiedere che, dati due qualsiasi eventi
Ei ed Ej elementari (quindi incompatibili) di Ω si abbia
P(Ei v Ej) = P(Ei) + P(Ej)
(1)
(Il simbolo v sta per “oppure”)
Per la dimostrazione si veda ad esempio Daboni (1967). Un esempio numerico può però
convincere di come il mancato rispetto della proprietà (1) porti alla possibilità di effettuare
arbitraggi, cioè all’incoerenza. Supponiamo di scommettere sul realizzarsi, separatamente,
degli eventi E1 ed E2 valutati con probabilità P(E1)=P(E2)=0.2. Nel contempo supponiamo
di accettare una scommessa (in qualità di banco) sull’evento
E1 v E2 valutato con
probabilità P(E1 v E2) = 0.5 (ovvero maggiore di P(E1) + P(E2)). In questo caso oggi pago
0.2+0.2 ma intasco 0.5 pertanto ho in tasca +0.1; in futuro, se uno dei due eventi si
realizza ottengo 1 (per aver scommesso) e pago 1 (per aver accettato la scommessa), se
nessun evento si realizza non ricevo nulla e non devo pagare. In conclusione: oggi intasco
0.1 e in futuro sono in ogni caso in pareggio, pertanto complessivamente ottengo un
guadagno certo di 0.1 (arbitraggio).
2.4
Conseguenze della coerenza
n
•
Poiché E1 v E2 v…En = Ω si ha:
P(Ω) =
∑
P(Ei) = 1
i =1
•
L’evento EC (complementare di E) che si realizza se e solo se non si realizza E, ha
probabilità
P(EC) = 1 – P(E)
infatti per mantenere la coerenza deve essere P(E v EC) = P(E) + P(EC) ma P(E v EC) = 1,
perché almeno uno dei due si realizzerà certamente, da cui la proprietà.
13
2.5
Alcuni esempi
LANCIO DI UNA MONETA
Vogliamo calcolare la probabilità di ottenere “Testa” e quella di ottenere “Croce” col lancio
di una moneta. In questo caso lo spazio degli eventi è Ω = {T,C} (T= si realizza testa; C= si
realizza croce). L’insieme delle parti è P(Ω) = {Ø, T, C, Ω }. La coerenza impone
P(T) + P(C) = 1
Questa relazione non ci consente di calcolare separatamente P(T) e P(C). A questo
scopo, occorre un’osservazione “esterna”.
Se la moneta ci appare del tutto simmetrica, ovvero non è truccata, non vediamo a priori
alcun motivo per attribuire a uno dei due esiti una probabilità maggiore o minore di quella
dell’altro. Perciò ci sentiamo autorizzati ad assumere:
P(T) = P(C) .
Le due relazioni, insieme, risolvono ora il problema della determinazione delle due probilità
fornendo:
P(T) = P(C) = ½ .
LANCIO DI DUE O PIU’ MONETE
Lanciamo due monete (o la stessa moneta due volte) e studiamo la probabilità che si
presenti testa sia al primo che al secondo lancio.
Vogliamo, in altre parole, calcolare P(TT). Poiché le realizzazioni possibili del lancio di due
monete sono TC, CC, CT, TT, mentre l’unico caso favorevole è TT, per motivi di simmetria
dell’informazione analoghi a quelli del caso del lancio di una singola moneta valutiamo
P(TT) = ¼ .
La probabilità che si presenti una testa su due lanci effettuati è invece ½
Lanciando tre monete qual è la probabilità che si presenti almeno una croce?
Se consideriamo distintamente le tre monete, allora si presentano 8 casi egualmente
probabili: TTT, TTC, TCT, CTT, CTC, CCT, CCC. Soltanto nel primo caso non si hanno
croci, quindi la valutazione di probabilità richiesta è ⅞.
LANCIO DI UN DADO
Assegniamo la probabilità a ciascuno dei sei possibili esiti del lancio di un dado:
Ω = {f1, f2, f3, f4, f5, f6}
Indicando con fi la faccia del dado sulla quale sono incisi i punti. Abbiamo
14
6
∑
P(fi) = 1
i =1
Inoltre, se il dado non presenta alcuna deformità evidente, non c’è motivo di pensare che i
diversi esiti abbiano probabilità differenti. Da ciò segue:
P(fi) =
1
6
per ogni i .
Negli esempi affrontati, abbiamo invocato una ragione di “simmetria”, che può esprimersi
come condizione a priori sulla distribuzione di probabilità. In tal caso tutti gli eventi
elementari considerati vengono ad avere la stessa valutazione di probabilità, sono ritenuti,
cioè, equiprobabili.
ALTRI ESEMPI
Determiniamo la probabilità P per ciascuno dei seguenti eventi:
a)
nel lancio di un dado si presenta un numero pari.
L’evento può verificarsi in tre modi (un 2, un 4, un 6) su 6 casi equiprobabili: P(pari) = ½ ;
b)
nel lancio di un dado si presenta 1 oppure 2.
Essendo P(1 v 2) = P(1) + P(2) si ha P(1 v 2) = ⅓.
c)
lanciando una moneta e un dado si presentano Testa e un numero pari.
Essendo i casi possibili 12 (T1, T2, T3, T4, T5, T6, C1, C2, C3, C4, C5, C6), mentre i casi
favorevoli sono 3 (T2, T4, T6), la probabilità è data da P(T,pari) = ¼.
15
2.6
Misura della probabilità nel caso di eventi compatibili
Siano dati lo spazio campionario Ω e due suoi sottoinsiemi A e B costituiti da più eventi
elementari:
Ω
A = E1 ∪ E2 ∪ E3
∪
(Il simbolo
B = E3 ∪ E4 ∪ E5
sta per “unione” ed è equivalente a v)
Qual è la probabilità P(A ∪ B)? In questo caso A e B (eventi compatibili, data la loro
possibile contemporanea realizzazione) hanno in comune l’evento E3, per cui la probabilità
non è più P(A ∪ B) = P(A) + P(B), altrimenti verrebbe conteggiato due volte E3,
intersezione di A e B. Vale infatti il seguente teorema:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Teorema
(2)
∩ sta per “intersezione”)
Dimostrazione. L’insieme A ∪ B è l’unione dei 3 eventi incompatibili A ∩ BC, A ∩ B e AC ∩ B.
(Il simbolo
Si ha
P(A ∪ B) = P(A ∩ BC)+P(A ∩ B)+P(AC ∩ B) =
= [P(A ∩ BC)+P(A ∩ B)]+[P(AC ∩ B)+ P(A ∩ B)] - P(A ∩ B) =
= P(A) + P(B) - P(A ∩ B) .
2.7
□
Probabilità condizionate o subordinate
Immaginiamo che lo spazio campionario Ω si riduca ad un suo sottoinsieme proprio H ⊂ Ω.
Graficamente:
16
Ω
Il realizzarsi dell’evento H costringe a rivedere la probabilità da assegnare alla
realizzazione dell’evento E: E dato H (si scrive E|H), ha una probabilità P(E|H) che in
generale sarà diversa rispetto a P(E).
Nell’approccio assiomatico la probabilità condizionata è definita ponendo
P(E|H) =
ovvero
P( E ∩ H )
P( H )
P(E ∩ H) = P(E|H) P(H).
Utilizzando l’approccio soggettivo alla probabilità tale formula può essere dimostrata. In
termini di quote eque essa può essere riscritta come
1
1
1
=
⋅
q( E ∩ H ) q( E | H ) q( H )
ovvero
q(E ∩ H) = q(E|H) q(H) .
Dimostriamo quest’ultima versione della formula.
Consideriamo un esperimento che si svolge negli intervalli di tempo [0, t1] e [t1,t2].
Supponiamo di giocare una unità monetaria al tempo 0 sulla realizzazione dell’evento H al
tempo t1, ottenendo in caso di vittoria la quota q(H) e di puntare al tempo t1 tutta
l’eventuale vincita sulla realizzazione dell’evento E al tempo t2.
H
0
t1
E|H
t2
In caso di vittoria, vale a dire se E|H si realizza al tempo t2, potremo intascare la quota
q(E|H) moltiplicata per la quantità giocata q(H).
Pensiamo ora di giocare un’unità monetaria al tempo 0 sulla realizzazione dell’evento
H ∩ E al tempo t2, ottenendo in caso di vittoria la quota q(H ∩ E). Si tratta di una
scommessa diversa ma equivalente alla precedente nel senso che comporta una vittoria
17
esattamente negli stessi casi. L’equità nella valutazione della probabilità soggettiva chiede
allora che sia q(E ∩ H) = q(E|H) q(H), come volevamo dimostrare.
2.8
•
□
Alcune osservazioni
Evidentemente la formula
•
P(E|H) =
P( E ∩ H )
P( H )
chiede che la probabilità che si realizzi l’evento H sia diversa da 0.
Se l’evento H si realizza certamente, P(H)=1, allora P(E|H) = P(E). Più interessante è
il caso 0<P(H)<1, in cui si ha P(E|H) > P(E ∩ H).
•
Osserviamo che
E = (E ∩ H) ∪ (E ∩ HC). Poiché E ∩ H ed E ∩ HC sono disgiunti
risulta P(E) = P(E ∩ H) + P(E ∩ HC). Ma essendo P(E ∩ H) = P(E|H) P(H) possiamo
scrivere
P(E) = P(E|H) P(H) + P(E| HC) P(HC).
•
Confrontiamo le due probabilità P(E|H) e P(E) in un caso particolare.
Consideriamo gli eventi
E = la cantante Alexia vince il Festival di Sanremo
H = una donna vince il Festival di Sanremo
In questo caso evidentemente sarà P(E|H) > P(E).
Se, invece
H = un uomo vince il Festival di Sanremo
allora P(E)>P(E|H) = 0.
In generale non esiste alcuna relazione particolare che lega le due probabilità
considerate:
o se P(E/H) > P(E) si dice che E è positivamente correlato ad H,
o se P(E/H) < P(E) si dice che E è negativamente correlato ad H,
o se P(E/H) = P(E) si dice che E è indipendente da H.
•
Nel caso di eventi indipendenti si può scrivere
P(E) = P(E/H) =
P( E ∩ H )
P( H )
18
da cui:
P(E ∩ H) = P(E) P(H)
ovvero, la probabilità che i due eventi, E ed H, si verifichino contemporaneamente
corrisponde al prodotto delle loro probabilità di realizzazione.
2.9
•
Esempi
Lanciando due monete di seguito, consideriamo la probabilità di ottenere testa al
secondo lancio, dato che si è ottenuto testa anche al primo. Essendo i due lanci
indipendenti, l’informazione a nostra disposizione non influenza la valutazione finale:
P(T2|T1) = P(T2) = ½ .
•
Determiniamo la probabilità che, lanciando due volte un dado, si verifichi l’evento
E= la somma dei punti ottenuti nei lanci è 3
Avendo in tutto 36 possibili esiti, dei quali solo due [(1,2); (2,1)] ci permettono di avere
somma 3 si ha P(E)=2/36.
Consideriamo ora l‘evento
H= al primo lancio è uscito il numero 1.
Se H si realizza allora lo spazio campionario si riduce e si ottiene:
P(E|H) =
•
P( somma = 3 ∩ lancio1 = 1) 1 / 36 1
=
=
P(lancio1 = 1)
1/ 6 6
Determiniamo, lanciando sempre due dadi, le probabilità degli eventi
A = almeno un dado presenta il numero 3
B = la somma è 4.
Utilizziamo la formula (2): P(A) = P(lancio1=3 v lancio2=3) =
=P(lancio1=3)+P(lancio2=3) – P(lancio1=3 ∩ lancio2=3) =
1
1
1 11
+
=
6
6 36 36
Inoltre
P(B) = P((1,3);(3,1);(2,2))=
Da cui otteniamo
3
36
P(A ∪ B) =
P(A ∩ B) = P((1,3);(3,1))=
11
3
2
1
+
=
.
36
36 36
3
2
36
19
2.10
Teorema di Bayes
Se nelle formule precedenti scambiamo i ruoli degli eventi E ed H otteniamo
P( H ∩ E )
P( E )
P(H|E) =
che può essere scritta anche:
P(H ∩ E) = P(H|E) P(E)
Ovviamente P(H ∩ E) = P(E ∩ H), pertanto possiamo scrivere:
P(E|H) P(H) = P(H|E) P(E)
Risulta allora dimostrato il seguente teorema.
Teorema di Bayes
P(H|E) =
P( E | H ) P( H )
P( E )
2.11 Alcuni esempi di utilizzo del teorema di Bayes
Esempio 1
Supponiamo di dover decidere quale delle due imprese (Artsystem e Buonarroti S.r.l.) di
trasporto di opere d’arte contattare per l’allestimento della nostra mostra temporanea.
Sappiamo che la probabilità di rottura o danneggiamento delle opere è del 5% per
l’impresa A su un totale di 800 pezzi trasportati e del 10% su un totale di 1000 opere
trasportate per l’impresa B, alla fine del loro viaggio. Qual è la probabilità che un’opera sia
stata trasportata da A se l’opera ha effettivamente subito dei danni? Ovvero, quanto vale
P(A|Danni)?
E’ utile alla risoluzione del problema, ricorrere al cosiddetto albero di probabilità.
Il diagramma ad albero è un mezzo usato, in generale, per enumerare tutti i possibili esiti
di una serie di esperimenti, dove ciascun esperimento può avere un numero finito di esiti.
Esso viene costruito da sinistra a destra e, ad ogni nodo, il numero dei rami verso destra
corrisponde ai possibili esiti dell’esperimento successivo.
Nel nostro caso:
a)
la probabilità che un’opera venga trasportata da A è
800 4
=
1800 9
b)
la probabilità che un’opera venga trasportata da B è
1000 5
=
1800 9
20
A questo punto, per conoscere P(A|D), dobbiamo ricorrere alla formula di Bayes:
P(A|D) =
P( D | A) P( A)
P( D)
Conosciamo P(D|A) = 0.05 e P(A) =4/9 , ci resta da valutare P(D) sommando tutti i rami
che portano all’esito D:
P(D) = P(D ∩ A) + P(D ∩ B) = P(D/A) P(A) + P(D/B) P(B)
Pertanto
0.05 ⋅
P(A|D) =
0.05 ⋅
4
9
4
5
+ 0.1 ⋅
9
9
≅
2
7
Esempio 2
Al museo di Oslo, nonostante le efficienti misure di sicurezza, sono stati sottratti, nel mese
di agosto 2004, alcuni dipinti del pittore norvegese Edward Munch.
Vengono arrestati due uomini (Arsenio Lupin e BonBon) sospettati di aver commesso il
reato. Soggettivamente, giudichiamo maggiormente probabile che il furto sia stato
compiuto da A:
P(A) = 0.6, P(B) = 0.4 .
Disponiamo però di una macchina della verità che fornisce indicazione di innocenza con
probabilità del 90% per chi è realmente innocente e con probabilità del 20% per un
colpevole2. Desideriamo conoscere la probabilità che, qualora A superi il test e B non ce la
faccia, A sia il ladro.
Costruiamo l’albero di probabilità:
2
Il fatto che A superi il test dipende esclusivamente dal suo essere o meno il colpevole, non dai risultati ottenuti, al
medesimo test, da B. Ciò consente, qualora avessimo stabilito, ad esempio, l’innocenza di A, di calcolare la probabilità
che A e B superino entrambi il test come prodotto (0.2)(0.9), che A superi il test e B no [(0.2)(0.1)], e così via.
21
La probabilità che A sia il ladro, dato che A ha superato il test e B no, in base alla formula
di Bayes è:
P(A|A supera B, non supera)
=
P(A supera B, non supera | A) P(A)
=
P(A supera B, non supera)
=
(0.2 ⋅ 0.1) ⋅ 0.6
0.012
=
= 0.04
(0.2 ⋅ 0.1) ⋅ 0.6 + (0.9 ⋅ 0.8) ⋅ 0.4
0.3
La nuova informazione costringe pertanto a spostare la valutazione della probabilità di
colpevolezza di A al 4% contro il 60% della probabilità stabilita inizialmente.
Analogamente, volendo valutare la probabilità che A sia il ladro nel caso in cui A non abbia
superato il test, mentre B vi sia riuscito si ottiene
P(A|A non supera, B supera) =
(0.8 ⋅ 0.9) ⋅ 0.6
0.432
=
≅ 0.98 .
(0.8 ⋅ 0.9) ⋅ 0.6 + (0.1 ⋅ 0.2) ⋅ 0.4 0.44
22
3. Criteri decisionali in condizioni di rischio
Introduzione
Torniamo a considerare una matrice dei payoff, contenente i risultati economici Mij,
espressi in termini di utilità (o, più semplicemente, profitto) corrispondenti al realizzarsi
dello stato di natura sj avendo in precedenza optato per la decisione di. Supponiamo ora di
essere in grado di attribuire delle probabilità riguardo alla realizzazione dei diversi scenari
(Pj = probabilità di realizzazione di sj):
s1
...
sj
d1
.
...
.
di
. . .
Mij
P1 ...
Pj
...
sn
...
Pn
...
dm
Si parla in tal caso di decisioni in condizioni di rischio: esaminiamo ora alcuni tra i più noti
criteri di scelta in tali ipotesi.
Considereremo come esempio la tabella seguente:
3.1
s1
s2
s3
d1
6
9
1
d2
13
7
6
d3
2
8
9
P
0.1
0.6
0.3
Criterio della massima verosimiglianza
Si opta per l’alternativa che fornisce il payoff massimo in corrispondenza dello scenario
con più elevata probabilità di realizzazione.
23
Nell’esempio, lo scenario con più alta probabilità di realizzazione è s2 (probabilità 0.6):
optiamo per d1 che fornisce utilità 9.
Più in generale:
a) calcoliamo per quale scenario j* si ha Pj* = max Pj
j
b) si opta per la decisione di* tale che Mi*j*= max Mij*
i
3.2 Criterio del valore atteso (o dell’utilità attesa)
Si opta per l’alternativa che fornisce il massimo valore atteso delle utilità (massima utilità
attesa).
L’utilità attesa della decisione di è definita da:
n
E(di) =
∑
Mij Pj
j =1
La scelta cade dunque sulla decisione di* tale che
E(di*) = max E(di) .
i
Nell’esempio si ottiene:
E(d1) = 6·0.1 + 9·0.6 + 1· 0.3 = 6.3
E(d2) = 13·0.1 + 7·0.6 + 6·0.3 = 7.3
E(d3) = 2·0.1 + 8·0.6 + 9·0.3 = 7.7
La scelta cade allora su d3, mentre d1 è la decisione peggiore (mentre con il criterio della
massima verosimiglianza era la scelta migliore).
Si può notare che nel caso in cui gli scenari fossero equiprobabili il criterio del valore
atteso fornisce esattamente le stesse indicazioni del criterio della media aritmetica (criterio
di Laplace) visto in precedenza.
3.3
Criterio della probabilità di rovina
È data una soglia di utilità K al di sotto della quale il decisore è da ritenersi “in rovina”.
La probabilità di rovina relativa alla decisione di è data dalla somma delle probabilità
relative a tutte gli scenari sj per i quali si ha Mij ≤ K:
P di rovina(di) =
∑ Pj
Mij ≤α
Il criterio della probabilità di rovina indica come scelta per cui optare quella cui
corrisponde probabilità di rovina minore
P di rovina(di*) = min P di rovina(di)
i
Nell’esempio, fissata la soglia K=7, si ottiene:
24
P di rovina (d1) = 0.1 + 0.3 = 0.4
P di rovina (d2) = 0.6 + 0.3 = 0.9
P di rovina (d3) = 0.1
La decisione da prendersi è ancora d3.
3.4
Criterio della probabilità di fare fortuna
Fissata una soglia di utilità H al di sopra o in corrispondenza della quale “facciamo
fortuna”.
Definita la probabilità di fare fortuna relativa alla decisione di:
P di fortuna(di) =
∑ Pj
Mij ≥H
viene scelta la decisione di* per la quale è massima la probabilità di far fortuna:
P di fortuna(di*) = max P di fortuna(di)
i
Nell’esempio, fissata la soglia H=10, si ottiene:
P di fortuna (d1) = 0
P di fortuna (d2) = 0.1
P di fortuna (d3) = 0
La scelta cade allora su d2, che, con gli altri criteri, non era mai apparsa opportuna.
3.5
Alcune osservazioni sul valore atteso.
Consideriamo la tabella seguente
s1
s2
d1
50
40
d2
90
10
P
0.5
0.5
I valori attesi delle due decisioni sono
E(d1) = 45
E(d2) = 50
25
La differenza tra le due utilità attese non è grande; la variabilità delle utilità è invece molto
più marcata, bassa con d1, con variazione 50 – 40=10, alta con d2, con variazione 90 –
10=80.
Altro esempio:
s1
s2
d1
50
40
d2
90
0
P
0.5
0.5
Ora si ha E(d1) = E(d2) = 45: nel caso fossimo “avversi al rischio”, sarebbe opportuno
scegliere d1.
Consideriamo ora:
s1
s2
d1
1000
1000
d2
1001
0
P
p
1-p
Si ottiene: E(d1) = 1000, E(d2) = 1001⋅ p + 0⋅ (1 – p) .
Utilizzando il criterio del valore atteso, la scelta cade su d2 quando
1001⋅ p > 1000, ovvero con p > 1000/1001 ≈ 0.999
Il criterio di massima verosimiglianza, al contrario, suggerisce di optare per d2, quando
p>1–p. Dunque, è sufficiente p = 0.501(vs p ≅ 0.999 del primo criterio), perché si scelga d2!
26
3.6
Valore atteso dell’informazione perfetta (EPI=expected value of perfect
information)
Supponiamo che per un museo si prospettino tre possibili strategie che portano
all’aumento dell’offerta espositiva:
d1 = utilizzo dei magazzini, dopo opportuno adeguamento
d2 = costruzione di una nuova ala
d3 = affitto di alcune sale di un edificio adiacente
In seguito, vengono valutati i possibili profitti, ipotizzando quattro possibili scenari:
s1 = domanda molto elevata
s2 = domanda elevata
s3 = domanda media
s4 = domanda bassa
La matrice dei payoff, comprensiva delle probabilità di realizzazione degli scenari, è la
seguente:
s1
s2
s3
s4
150
110
60
-40
101.00
d1
d2
E
-210 171.00
280
200
100
70
47.5
20
-5
0.4
0.3
0.2
0.1
d3
P
45.75
Sulla base di queste informazioni, con il criterio del valore atteso si sceglie d*= d2 .
Supponiamo, ora, di poter ottenere nuove informazioni, in particolare un esperto sia in
grado di dirci esattamente quale stato di natura si realizzerà e sia disposto a venderci tali
informazioni: fino a quale prezzo siamo disposti a pagare?
Cerchiamo di stabilire un prezzo limite, al di sopra del quale non siamo più disposti a
comperare l’informazione.
27
Se avessimo l’informazione, a seconda dello scenario indicato come certo dall’esperto
sceglieremmo ovviamente la decisione che presenta, in corrispondenza di tale scenario, la
massima utilità. Nell’esempio avremmo: s1 , s2 , s3 → d2 ; s4 → d3 .
Poiché non sappiamo quale scenario ci verrà indicato possiamo solo valutare il valore
atteso dell’utilità che la nuova informazione può procurare:
V = 280⋅0.4 + 200⋅0.3 + 100⋅0.2 - 5⋅0.1 =191.5
Essendo V > E(d*) = E(d2) la differenza tra V e E(d2) rappresenta il vantaggio mediamente
ottenibile nel caso in cui disponessimo dell’informazione perfetta, quindi è questo il prezzo
massimo che siamo disposti a pagarla:
EPI = V – E(d*)
Nell’esempio si ha:
EPI = 191.5 – 171 = 20.5.
3.7 Valore atteso dell’informazione campionaria (EIC)
Supponiamo di poter riuscire ad ottenere delle informazioni mediante un’indagine
campionaria, anziché utilizzando le conoscenze di un esperto. L’indagine campionaria
ovviamente comporta dei costi e si rende necessario decidere se investire o meno e fino a
quale budget utilizzare.
Consideriamo un esempio numerico relativo ad un sistema di prenotazione/vendita online
dei biglietti di un museo. Assumiamo che si possa verificare uno fra gli scenari
s1 = domanda alta,
s2 = domanda bassa.
e con matrice dei payoff:
s1
s2
d1
10
-20
d2
2
0
P
0.6
0.4
E
-2
1.2
Dove d1 è la decisione di investire, d2 è la decisione di non investire nella nuova attività.
Con il criterio del valore atteso la scelta ottima è di non investire in questa nuova attività.
Immaginiamo, però, di condurre un’indagine di mercato per ottenere indicazioni più
aggiornate relativamente al realizzarsi degli scenari. Sulla base della nostra esperienza
precedente, sappiamo che una tale strategia fornisce indicazioni sulla domanda reale con
diversi livelli di attendibilità, riassunti dalla seguente matrice dei payoff:
28
Esito del test
Mercato favorevole Mercato non favorevole
Domanda reale
ts1
s1(alta)
0.8
s2(bassa)
0.4
ts2
0.2
0.6
I valori della tabella rappresentano la probabilità subordinata:
P(test=tsj|domanda reale=si)
Chiediamoci, per esempio, quale sia la probabilità che la domanda reale sia alta, dato che
l’indagine indica uno scenario favorevole, vogliamo cioè P( s1 | ts1 ).
Applicando la formula di Bayes:
P(s1 | ts1) =
P(ts1 | s1) P(s1)
P(ts1)
da cui anche
=
P(ts1 | s1) P(s1)
P(ts1| s1) P(s1) + P(ts1 | s2) P(s2)
0.8 ⋅ 0.6
= 0.75
(0.8 ⋅ 0.6) + (0.4 ⋅ 0.4)
P(s2|ts1) = 1 – 0.75 = 0.25 essendo i due eventi incompatibili (la domanda
è alta oppure bassa).
Invece
P(s2 | ts2) =
=
P(ts2 | s2) P(s2)
P(ts2)
=
0.4 ⋅ 0.6
2
= 0.6 =
(0.4 ⋅ 0.6) + (0.6 ⋅ 0.2)
3
da cui: P(s1| ts2) = 1 – 2/3=1/3.
29
Osserviamo infine che P(ts1) = (0.8 ⋅ 0.6) + (0.4 ⋅ 0.4) = 0.64 e P(ts2) = 1 – 0.64 = 0.36 .
Supponiamo, adesso, che l’indagine indichi un mercato effettivamente favorevole (si
realizza ts1); ricostruiamo, allora, la matrice dei payoff con le diverse probabilità di
realizzazione degli scenari, P(si | ts1), e i corrispondenti valori attesi:
s1
s2
E
d1
10
-20
2.5
d2
2
0
1.5
0.75
0.25
P(si | ts1)
Analogamente nel caso di una indicazione di mercato non favorevole:
s1
s2
E
d1
10
-20
-10
d2
2
0
2/3
P(si | ts2)
1
3
2
3
Il valore atteso con l’informazione campionaria sarà, quindi:
W = P(ts1)·2.5+ P(ts2) ·2/3 = 0.64·2.5 + 0.36 ·2/3 =1.84
Il valore atteso dell’informazione campionaria è allora
EIC = W – E(d*)
che nel nostro caso porge
EIC = 1.84 – 1.20 = 0.64 . Si tratta del massimo prezzo che saremo
ragionevolmente disposti a pagare per effettuare l’indagine ed ottenere, così,
l’informazione.
Naturalmente il valore atteso dell’informazione campionaria è inferiore rispetto al valore
atteso dell’informazione perfetta. In particolare nell’esempio si ha
EPI= V-E(d*) = (0.6·10)+(0.4·0) -1.2 = 6-1.2 = 4.8 .
30
Bibliografia
Anderson, Sweeney, Williams, An introduction to management science, South Western
College Publishing, 2000.
Daboni L., Elementi di calcolo delle probabilità, Boringhieri, Torino, 1967.