INTEGRATORE E DERIVATORE REALI
-Schemi elettrici:
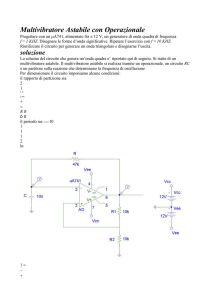
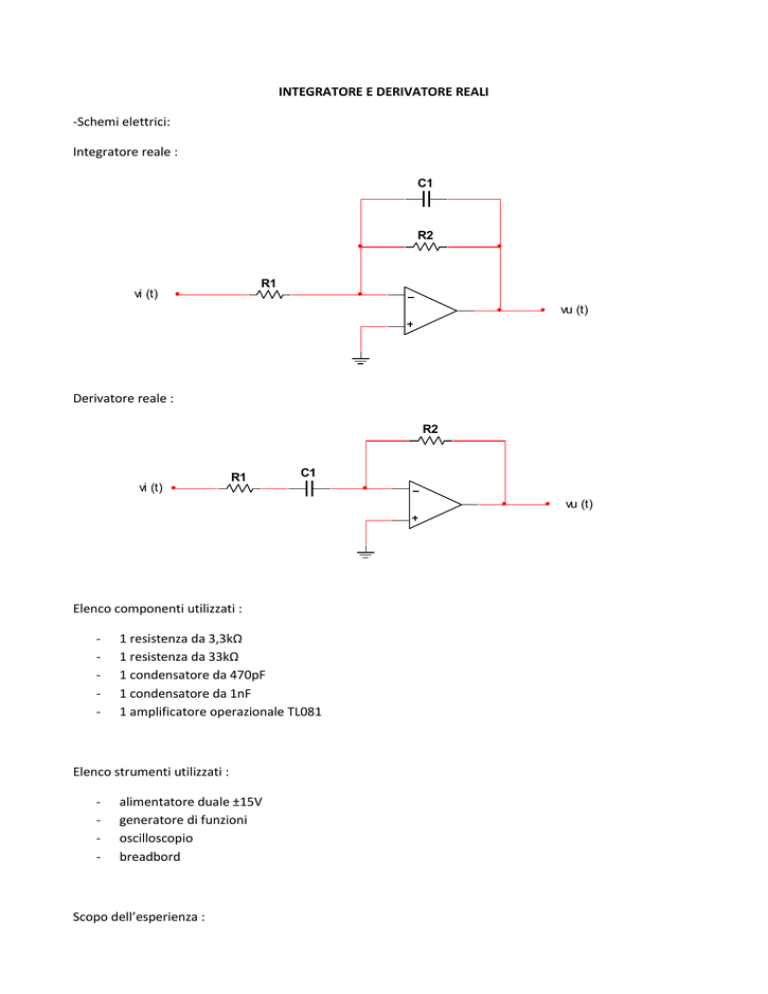
Integratore reale :
C1
R2
R1
vi (t)
vu (t)
Derivatore reale :
R2
vi (t)
R1
C1
vu (t)
Elenco componenti utilizzati :
-
1 resistenza da 3,3kΩ
1 resistenza da 33kΩ
1 condensatore da 470pF
1 condensatore da 1nF
1 amplificatore operazionale TL081
Elenco strumenti utilizzati :
-
alimentatore duale ±15V
generatore di funzioni
oscilloscopio
breadbord
Scopo dell’esperienza :
Verificare in laboratorio il funzionamento di integratore e derivatore reali .
Cenni teorici:
-Integratore invertente:
L’integratore è un circuito che permette di ottenere in uscita l’integrale rispetto al tempo del segnale di
ingresso. Il circuito dell’integratore ideale di Miller, è il seguente:
Esso ricorda la connessione invertente di un operazionale, in cui però la resistenza di reazione R2 è stata
sostituita da un condensatore, C, nel quale, per il fatto che un operazionale ideale non assorbe corrente ai
propri ingressi, scorre la stessa corrente (i) che scorre nella resistenza R. Inoltre, sempre perché
l’operazionale viene considerato ideale, la differenza di potenziale fra i terminali invertente e non
invertente è uguale a zero e perciò il terminale invertente è come se fosse collegato a massa virtuale; la
corrente circolante in R vale quindi :
ricordando che la tensione ai capi di un condensatore (considerandolo inizialmente scarico) è data da:
e sapendo che la tensione di uscita è
otteniamo:
E’ dimostrato quindi che la tensione di uscita di questo circuito è l’integrale del segnale di ingresso
moltiplicato per un certo fattore
.
Se il condensatore fosse inizialmente carico a una certa tensione
, otteniamo :
L’inconveniente di questo circuito è che può andare facilmente in saturazione, a causa di disturbi a basse
frequenze che potrebbero arrivare all’ingresso dell’operazionale; infatti per la frequenza del disturbo che
tende a zero, la reattanza del condensatore tende a infinito, il condensatore diventa quindi un circuito
aperto; l’operazionale è come se fosse connesso in catena aperta e la sua amplificazione è quindi infinita,
arrivando così alla saturazione.
Per ovviare a questo fenomeno, si inserisce in parallelo al condensatore una resistenza (e questo è il
circuito da noi utilizzato, che ho inserito all’inizio), in modo che il guadagno massimo dell’operazionale sia
limitato al valore Av = -R2/R1. La R2 deve essere dimensionata in maniera tale che alla frequenza di lavoro
dell’integratore la sua resistenza sia trascurabile (e quindi molto maggiore) rispetto alla reattanza del
condensatore; possiamo scrivere che perché il circuito funzioni da integratore dobbiamo avere:
Dove f è la frequenza di lavoro dell’integratore; si noti che il circuito da noi considerato, svolge anche la
funzione di filtro passa basso, infatti
è proprio la frequenza di taglio del filtro; possiamo dire
quindi che perché questo circuito funzioni da integratore, la frequenza del segnale di ingresso deve essere
molto maggiore della frequenza di taglio, detta anche frequenza critica. In genere si pone la frequenza di
lavoro a 10*fc, con fc la frequenza critica.
-Derivatore invertente:
Il derivatore è un circuito che permette di ottenere in uscita la derivata rispetto al tempo del segnale di
ingresso.
Il circuito del derivatore ideale è il seguente :
Esso parte sempre dalla connessione invertente di un operazionale, in cui però la resistenza R1 è stata
sostituita da un condensatore, C; nella resistenza di reazione R scorre la stessa corrente che scorre nel
condensatore, per la stessa considerazione effettuata per l’integratore e cioè che gli ingressi
dell’operazionale ideale non assorbono corrente. Inoltre, dato che il potenziale invertente è come se fosse
connesso a massa virtuale, la tensione sul condensatore coincide con la tensione di ingresso e la tensione di
uscita è data da –R*i. Ricordando che la relazione che lega la corrente circolante nel condensatore alla
tensione ai suoi capi è:
otteniamo:
Abbiamo così dimostrato che in questo circuito il segnale di uscita è la derivata rispetto al tempo del
segnale di ingresso; anche il derivatore ideale, appunto perché tale, non può essere usato “così com’è” ma
ha bisogno di opportune modifiche perché funzioni correttamente. Infatti, se ipotizziamo che in ingresso
abbiamo un disturbo ad alta frequenza, l’operazionale va in saturazione, perché il condensatore diventa un
cortocircuito e l’amplificazione diventa infinita; per ovviare a questo problema, si pone una resistenza in
serie al condensatore C, in modo da ottenere il circuito da noi utilizzato che ho inserito alla prima pagina;
l’amplificazione risulta così limitata al rapporto –R2/R1 anche nel caso in cui vi siano disturbi di alta
frequenza all’ingresso dell’operazionale. Lo stesso discorso fatto per l’integratore, vale per il derivatore: alla
frequenza di lavoro, la resistenza R1 deve avere valore trascurabile rispetto alla reattanza del
condensatore, e quindi dato che i due elementi sono in serie, la reattanza del condensatore deve essere
molto maggiore rispetto alla resistenza.
Otteniamo quindi:
Dove f è la frequenza di lavoro del derivatore; si noti che il circuito da noi considerato, svolge anche la
funzione di filtro passa alto, infatti
è proprio la frequenza di taglio del filtro; possiamo dire
quindi che perché questo circuito funzioni da derivatore, la frequenza del segnale di ingresso deve essere
molto minore della frequenza di taglio, detta anche frequenza critica. In genere si pone la frequenza di
lavoro a 1/10 della frequenza di taglio.
Ci è stato richiesto di progettare un integratore e un derivatore, avendo la frequenza di taglio di ciascuno e
di verificare il loro comportamento per diverse frequenze del segnale in ingresso.
-Dimensionamento dei componenti dell’integratore:
Per l’integratore, ci è stata richiesta una frequenza di taglio di 10kHz; abbiamo posto l’amplificazione, cioè il
rapporto R2/R1 uguale a dieci, in modo che in banda passante (cioè prima dei 10kHz, dato che l’integratore
è un filtro passa basso) il circuito potesse accettare in ingresso tensioni di 1Vmax (cioè 2Vpp), ottenendo in
uscita 10Vmax, senza correre il rischio che l’operazionale vada in saturazione. Abbiamo posto R1 = 3,3k e
R2 = 33k, mantenendo tali valori di resistenze anche per il derivatore. Ci siamo calcolati poi il valore della
capacità da porre in parallelo alla R2, in modo da ottenere la frequenza di taglio richiesta:
Abbiamo approssimato al valore commerciale 470pF; la frequenza di taglio varia di poco, dai 10kHz richiesti
ci ritroviamo :
Di ciò terremo conto nell’effettuare le misure, considerando la frequenza di taglio non più 10kHz ma
10,26kHz.
-Dimensionamento dei componenti del derivatore:
Per il derivatore, ci è stata richiesta una frequenza di taglio di 50kHz; abbiamo mantenuti invariati i valori di
R1 e R2; ci siamo calcolati il valore della capacità da porre in serie alla R1, in modo da ottenere la frequenza
di taglio richiesta:
Abbiamo approssimato al valore commerciale 1nF; la frequenza di taglio varia, dai 10kHz richiesti ci
ritroviamo :
Di ciò terremo conto nell’effettuare le misure, considerando la frequenza di taglio non più 50kHz ma
48,23kHz.
Effettuare le misure sull’integratore:
Una volta progettato e montato il circuito su breadbord, applichiamo all’ingresso dell’integratore un
segnale ad onda quadra, con le frequenze riportate in tabella; ci siamo ricavati quindi, per ogni valore di
frequenza, la forma d’onda in uscita al circuito e la tensione d’uscita picco-picco. Se non fosse stata inserita
la R2, e sarebbe stato quindi possibile utilizzare un integratore ideale, il circuito avrebbe funzionato da
integratore per tutte le frequenze del segnale di ingresso, e quindi da un onda quadra avremmo ottenuto
sempre un’onda triangolare, per qualsiasi frequenza del segnale di ingresso : si ricordi infatti che l’integrale
di una costante rispetto al tempo è una retta di equazione m*t, dove m è il coefficiente angolare della
retta; quindi applicando al circuito un segnale ad onda quadra, a valor medio nullo e con duty cycle del
50%, in uscita otterremo un’onda triangolare, cioè un segnale formato da due rampe, una crescente
(ottenuta quando l’onda quadra assume valori negativi, perché il derivatore è invertente) e una
decrescente (ottenuta quando l’onda quadra assume valori positivi, per lo stesso motivo di prima). Tuttavia
noi abbiamo utilizzato l’integratore reale, e quindi il circuito non funzionerà da integratore per tutte le
frequenze del segnale di ingresso; il nostro compito è quello di verificare a che frequenza il circuito inizia a
funzionare da integratore.
Effettuare le misure sul derivatore:
Una volta progettato e montato il circuito su breadbord, applichiamo all’ingresso del derivatore un segnale
ad onda triangolare, con le frequenze riportate in tabella; ci siamo ricavati quindi, per ogni valore di
frequenza, la forma d’onda in uscita al circuito e la tensione d’uscita picco-picco. Se non fosse stata inserita
la R1, e sarebbe stato quindi possibile utilizzare un derivatore ideale, il circuito avrebbe funzionato da
derivatore per tutte le frequenze del segnale di ingresso, e quindi da un onda triangolare avremmo
ottenuto sempre un’onda quadra, per qualsiasi frequenza del segnale di ingresso : si ricordi infatti che la
derivata di una retta rispetto al tempo è il suo coefficiente angolare m; quindi applicando al circuito un
segnale ad onda triangolare, a valor medio nullo e con duty cycle del 50%, in uscita otterremo un’onda
quadra, che sarà positiva quando la rampa che forma l’onda triangolare sarà decrescente, e negativa
quando la rampa che forma l’onda triangolare sarà crescente ( si ricordi che il derivatore è invertente).
Tuttavia noi abbiamo utilizzato il derivatore reale, e quindi il circuito non funzionerà da derivatore per tutte
le frequenze del segnale di ingresso; il nostro compito è quello di verificare a che frequenza il circuito inizia
a funzionare da derivatore.
Nelle pagine successive, riporto le misure effettuate sui due circuiti, riportando per ciascuno di esso, per
ogni valore di frequenza del segnale di ingresso, i grafici delle forme d’onda ottenute in uscita e il loro
valore di ampiezza picco-picco. In ingresso, ad entrambi i circuiti è stato applicato un segnale di 2Vpp, per
essere certi di non mandare in saturazione l’operazionale.
Misure sull’integratore ( ft = 10,26kHz) :
Frequenza
1/20 ft
Grafico delle forme d’onda
Tensione di
uscita piccopicco
510 Hz
20Vpp
1/10 ft
1026Hz
20Vpp
ft
10,26kHz
18Vpp
2*ft
20,52kHz
13Vpp
10*ft
102,61kHz
3,2Vpp
20*ft
205,2kHz
1,8Vpp
Misure sul derivatore ( ft = 48,23kHz) :
Frequenza
20 ft
Grafico delle forme d’onda
Tensione di
uscita piccopicco
964,6kHz
20Vpp
10 ft
482,3kHz
20Vpp
ft
48,23kHz
11,5Vpp
1/10 ft
4,82kHz
1,3Vpp
1/20 ft
2,41kHz
0,65Vpp
-Commenti sulle misure effettuate sull’integratore :
Nell’integratore, si può notare come per basse frequenze del segnale di ingresso ad onda quadra, il segnale
di uscita rimane più o meno un’onda quadra, sfasata di 180 gradi rispetto a quella in ingresso (per l’uso
della connessione invertente), di ampiezza 10 volte maggiore (infatti l’amplificazione è 10) e con i fianchi in
salita e in discesa leggermente arrotondati; ciò avviene perché il circuito, essendo un filtro passa basso,
elimina le componenti più alte del segnale ad onda quadra, e quindi il segnale in uscita risulta leggermente
distorto rispetto a quello in ingresso; ciò avviene fino alla frequenza 1/10 ft. Trascurando la leggera
distorsione dell’onda quadra, possiamo dire che questo circuito fino alla frequenza 1/10 ft funziona come
amplificatore invertente, perché la reattanza del condensatore è trascurabile rispetto alla resistenza R2.
Alla frequenza di taglio invece, il segnale in uscita non è più quadro, perché sempre più armoniche
dell’onda quadra vengono eliminate e il segnale di uscita risulta parecchio distorto rispetto al segnale in
ingresso; qui inoltre la reattanza del condensatore non è più trascurabile rispetto alla resistenza R2:
all’aumentare della frequenza, la reattanza del condensatore diminuisce, e quindi anche l’amplificazione
diminuisce; infatti l’ampiezza picco-picco del segnale di uscita è inferiore rispetto alle ampiezze dei segnali
precedenti, con frequenza minore di ft. Ora notiamo che man mano che aumentiamo la frequenza del
segnale di ingresso, l’ampiezza picco-picco del segnale di uscita tende a diminuire, e inoltre esso tende a
diventare un’onda triangolare; possiamo affermare che il circuito inizia a funzionare da integratore a una
frequenza dieci volte quella di taglio, infatti a questa frequenza abbiamo in uscita un’onda triangolare; il
circuito funziona da integratore a 10*ft proprio perché la resistenza R2 è ora trascurabile rispetto alla
reattanza del condensatore, e quindi è come se non ci fosse, riportandoci nella condizione di integratore
ideale. Alla frequenza 20*ft, il segnale di uscita è sempre un’onda triangolare, ma di ampiezza minore:
questo perché il periodo dell’onda quadra diminuisce all’aumentare della sua frequenza, e siccome
l’ampiezza del segnale di uscita è data da
si nota come, al diminuire del tempo considerato, e cioè il periodo dell’onda quadra, diminuisce l’ampiezza
della tensione in uscita. Per cui la condizione di funzionamento dell’integratore alla frequenza 10*ft è un
buon compromesso fra la forma del segnale in uscita, che è perfettamente triangolare, e la sua ampiezza;
nella pratica, la frequenza 10*ft viene considerata la frequenza di lavoro dell’integratore. I risultati ottenuti
in laboratorio coincidono con quelli ottenuti con la simulazione mediante software.
-Commenti sulle misure effettuate sul derivatore:
Nel derivatore, si può notare che per alte frequenze del segnale di ingresso ad onda triangolare, il segnale
di uscita è sempre un segnale ad onda triangolare, sfasata di 180 gradi rispetto a quella in ingresso, sempre
per lo stesso motivo di cui ho discusso nell’integratore: per frequenze fino a 10*ft, nel derivatore il
condensatore in serie alla R1 ha reattanza trascurabile rispetto alla resistenza stessa, e la configurazione
circuitale approssima quella di un amplificatore invertente; alla frequenza ft, invece, la reattanza del
condensatore inizia “a farsi sentire”: l’ampiezza del segnale in uscita subisce una notevole attenuazione e
anche una distorsione, dovuta alla modifica delle ampiezze di alcune componenti del segnale ad onda
triangolare, soprattutto quelle più basse (perché il circuito è un filtro passa alto); ora notiamo che man
mano che diminuiamo la frequenza del segnale di ingresso, il segnale di uscita approssima sempre più
un’onda quadra. Infatti già a 1/10 ft la resistenza R1 è trascurbile rispetto alla reattanza del condensatore in
serie ad essa, e quindi si può non considerare, riportandoci alla condizione di derivatore ideale; tuttavia
notiamo che il segnale in onda quadra in uscita a 1/10 ft ha ancora i fianchi leggermente arrotondati; per
avere dei fianchi un po’ più ripidi, dobbiamo passare a 1/20 ft; nella pratica questa viene considerata la
frequenza di lavoro del derivatore; anche qui, tuttavia, aumentando la frequenza, diminuisce l’ampiezza del
segnale in uscita per le stesse osservazioni effettuate sull’integratore (utilizzando naturalmente le formule
del derivatore). I risultati ottenuti in laboratorio coincidono con quelli ottenuti con la simulazione mediante
software.