RETTE NEL PIANO
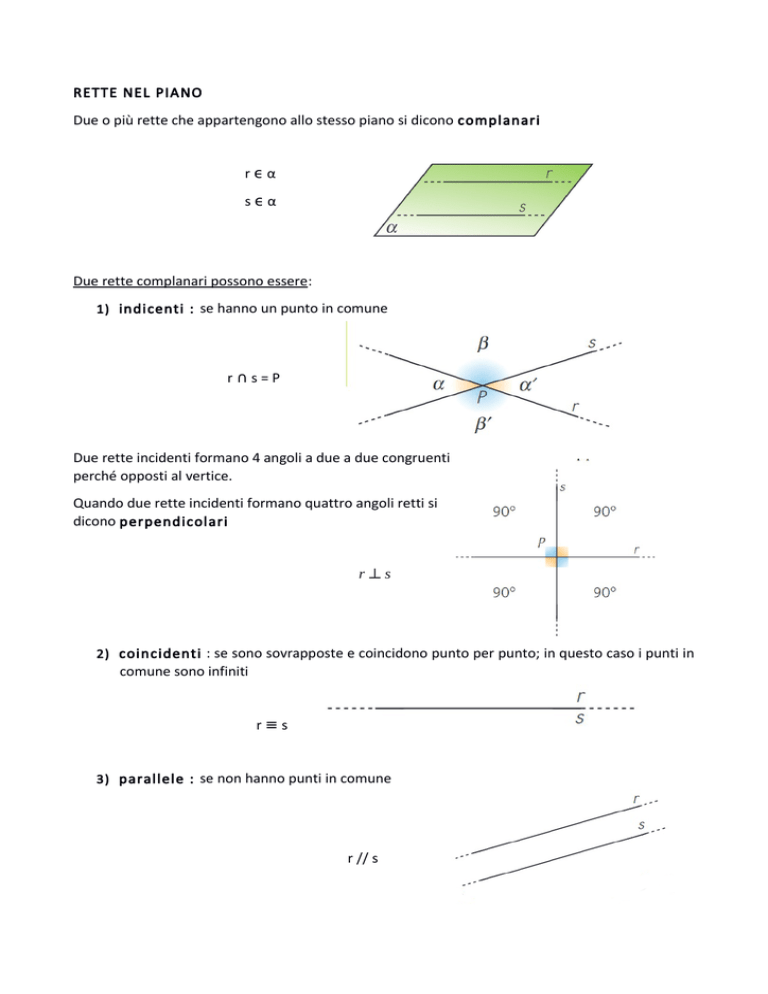
Due o più rette che appartengono allo stesso piano si dicono complanari
rϵα
sϵα
Due rette complanari possono essere:
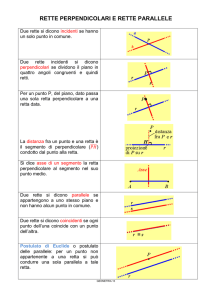
1) indicenti : se hanno un punto in comune
r∩s=P
Due rette incidenti formano 4 angoli a due a due congruenti
perché opposti al vertice.
Quando due rette incidenti formano quattro angoli retti si
dicono perpendicolari
r⊥s
2) coincidenti : se sono sovrapposte e coincidono punto per punto; in questo caso i punti in
comune sono infiniti
r≡s
3) parallele : se non hanno punti in comune
r // s
PROPRIETA’:
1) Perpendicolarità
Data una retta r ed un punto P esterno ad essa esiste UNA ED UNA SOLA retta passante per
P e perpendicolare a r
Il punto H di intersezione tra la
retta r e la perpendicolare è detto
piede della perpendicolare o
proiezione di P su r.
Il segmento PH è detto distanza del punto P dalla retta r e rappresenta il percorso più
breve possibile per raggiungere la retta partendo dal punto. Quindi scegliendo qualsiasi
altro punto Q sulla retta risulta che PH < PQ
→ La distanza di un punto da una retta è il segmento di perpendicolare
condotto dal punto alla retta
2) Postulato delle parallele
Data una retta r ed un punto P esterno ad essa esiste UNA ED UNA SOLA retta passante per
P e parallela a r
→ La distanza tra due rette parallele è un segmento che ha gli estremi sulle due rette ed è
perpendicolare ad entrambe le rette. I segmenti AH, BK e PL sono congruenti tra loro e
rappresentano la distanza tra le due rette parallele.
Due rette parallele mantengono sempre la stessa distanza
3)
Teoremi delle rette parallele tagliate da una trasversale
In generale, due rette r e s intersecate da una terza retta t , detta trasversale, formano otto angoli
che sono stati numerati da 1 a 8 in figura. Questi otto angoli vengono considerati a coppie a cui
vengono dati nei nomi particolari.
Coppie
Nome
3e6;4e5
alterni interni
1 e 8; 2 e 7
alterni esterni
6 e 2; 8 e 4; 5 e 1; 7 e 3
corrispondenti
6 e 4; 5 e 3
coniugati interni
8 e 2; 7 e 1
coniugati esterni
In generale queste coppie di angoli non sono congruenti tra loro. Ad esempio dall'immagine si
osserva che nella coppia di angoli alterni interni 3 e 6 l'angolo 3 è minore dell'angolo 6.
Se le rette tagliate da una trasversale sono parallele si può dimostrare che:
→ le coppie di angoli alterni interni, alterni esterni e corrispondenti sono congruenti
→ le coppie di angoli coniugati interni e coniugati esterni sono supplementari
coppie congruenti:
3 e 6 ; 4 e 5;
1 e 8; 2 e 7;
6 e 2; 8 e 4; 5 e 1; 7 e 3
coppie supplementari:
6 e 4; 5 e 3;
8 e 2; 7 e 1
Questo teorema vale anche al contrario ed è utile per capire in maniera rapida se due rette sono
parallele.
→ Se due rette intersecate da una trasversale formano 1 coppia di angoli alterni interni o alterni
esterni o corrispondenti congruenti oppure 1 coppia di angoli coniugati supplementari allora le
due rette sono parallele tra di loro.