Probl.discussione 2

Esercizi
Problemi di trigonometria con discussione
Problemi sui triangoli rettangoli
1 Considera una semicirconferenza di diametro AB e raggio unitario. Determina su di essa un punto P in modo che,
detta M la sua proiezione ortogonale sulla perpendicolare in B ad AB, risulti AP þ PM ¼ k.
bP ¼ x, si ottiene l’equazione 2 cos2 x 2 cos x þ k 2 ¼ 0, con 0 x ;
Posto BA
2
5
due soluzioni per 2 k 2
2 Determina la misura dell’angolo al vertice di un triangolo isoscele ottusangolo (non degenere), conoscendo il raggio r del cerchio circoscritto e la differenza kr tra il doppio della base e il triplo dell’altezza.
bC ¼ 2x si ottiene l’equazione 8 sin x cos x 6 cos2 x ¼ k
Sia ABC il triangolo inscritto, isoscele sulla base BC; posto BA
< x < ; una soluzione per 0 < k 1 e due soluzioni per 1 < k 2
con
4
2
3 In un triangolo rettangolo ABC (non degenere) l’ipotenusa BC misura 2a e il cateto AC è minore o uguale al cateto
AB. Detto O il punto medio di BC ed M il punto in cui la perpendicolare in O a BC incontra la retta AB, determina l’angolo ABbC in modo che l’area del rettangolo avente i lati congruenti ad AC e OM sia uguale a 2ka2 .
Posto ABbC ¼ x, si ottiene l’equazione cos2 x þ k cos x 1 ¼ 0 con 0 < x ;
4
pffiffiffi 2
1 soluzione per 0 < k 2
In un triangolo rettangolo ABC (non degenere) si ha BC ¼ 2a e ABbC ¼ x. Determina x in modo che la somma tra la
misura della mediana relativa al cateto AB e la misura della metà del cateto stesso valga ka.
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4 pffiffiffi
3
Si ottiene l’equazione 4 3 cos2 x ¼ k cos x, con 0 < x < ; due soluzioni per 2 < k 2
3
4
bB ¼ x in modo che, costruito il
Dato un cerchio di centro O e raggio r, determina un angolo al centro convesso AO
2
triangolo equilatero ABC sulla corda AB da parte opposta del centro, sia kr l’area del quadrilatero OACB.
pffiffiffi
pffiffiffi
Si ottiene l’equazione sin x 3 cos x ¼ 2k 3 con 0 x ;
pffiffiffi
pffiffiffi
pffiffiffi
3þ2
una soluzione per 0 k < 3 e due soluzioni per 3 k 2
8
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
5 Considera una semicirconferenza di diametro AB ¼ 2r. Determina una corda AC tale che, detta AD la corda che bi
bC, si abbia AC þ AD ¼ 2kr.
seca BA
bB ¼ 2x, con 0 x , si ottiene l’equazione 2 cos2 x þ cos x 1 ¼ k;
Posto CA
pffiffiffi
4
2
k2
una soluzione per
2
2
b
b
, determina l’angolo AOC ¼ 2x, dove C è un pun6 Dato un settore circolare AOB, di centro O, raggio r e ampiezza
3
_
to dell’arco AB, in modo che il rapporto tra i perimetri dei triangoli COB e AOC sia k.
pffiffiffi
Si ottiene l’equazione 3 cos x ð1 þ 2kÞ sin x þ 2 2k ¼ 0 con 0 x ;
3
pffiffiffi pffiffiffi
2þ 3
una soluzione per 2ð2 3Þ k 2
r
7 Dato un cerchio di raggio r, traccia una corda AB la cui distanza dal centro è . Determina, sul minore dei due archi
2
_
AB, un punto C in modo che sia soddisfatta la relazione: 2AC þ 3BC ¼ 2kr.
pffiffiffi
bB ¼ x, si ottiene l’equazione 2 sin x þ 3 cos x ¼ k con 0 x ;
Ponendo CA
pffiffiffi
pffiffiffi
3
pffiffiffi
pffiffiffi
3 3
3 3
e due soluzioni per
k 7
una soluzione per 3 k <
2
2
1/5
Problemi di trigonometria con discussione
,
3
è interna all’angolo convesso limitato dalle altre due ed è tale che la proiezione ortogonale di ogni suo punto sulla retta
cui appartiene c cade sulla semiretta c. Fissato sulla semiretta a il segmento unitario OA, siano B e C rispettivamente, le
proiezioni ortogonali di A su b e c. Determina l’angolo x formato dalle semirette a e c, sapendo che il triangolo BOC è
equivalente a un triangolo di base OA e altezza relativa di misura k.
pffiffiffi
1 pffiffiffi
Si ottiene l’equazione sin x cos x þ 3 cos2 x ¼ 4k con 0 x ; una soluzione per 0 k <
3;
2
4 pffiffiffi 1 pffiffiffi
2þ 3
due soluzioni per
3k
8
4
4
10 Un cateto di un triangolo rettangolo misura 2a e l’angolo acuto adiacente a esso ha coseno uguale a . Condotta
5
per il vertice dell’angolo retto una retta t che non attraversa il triangolo e indicata con x la misura dell’angolo che questa
retta forma con il cateto maggiore, determina x in modo che il volume del solido generato dal triangolo quando compie
una rotazione completa intorno alla retta t sia ka3 .
3
5
Si ottiene l’equazione 4 sin x þ 3 cos x ¼ 2k con 0 x ; una soluzione per k < 2; due soluzioni per 2 k 2
2
2
Le semirette a, b e c di origine comune O sono complanari. La semiretta a forma con la semiretta b un angolo di
9
a.
b.
c.
d.
ESERCIZI
11
Indicato con VV 0 un diametro di una sfera di centro O e raggio r, considera i seguenti quattro coni:
un cono di vertice O, asse OV 0 e base tangente alla sfera;
il cono opposto al vertice del precedente, avente la circonferenza di base sulla superficie sferica;
il cono di vertice V, asse VV 0 , apertura metà di quella dei due coni precedenti, e inscritto nella sfera;
il cono di vertice V 0 , inscritto nella sfera, e avente la stessa base di quella del terzo cono.
Indicati con V1 , V2 , V3 , V4 , rispettivamente i volumi dei quattro coni, determina l’angolo x di apertura del primo cono
in modo che sia soddisfatta la relazione:
V1 V2
V1 þ V2
ðk 3Þ
¼ 2k
V4
V3
Si ottiene l’equazione ð4 3kÞcos2 x þ ðk 2Þ cos x þ 4 k ¼ 0 con 0 < x < ; una soluzione per 2 < k 4;
2
pffiffiffiffiffiffi 30 þ 4 15
due soluzioni per 4 < k 11
Problemi sui triangoli qualunque
12
ESERCIZIO SVOLTO
_
Figura e scelta dell’incognita
_
Costruiamo una figura (fig. 1) e osserviamo che la posizione del punto P sull’arco BM resta univocamente individuata
bB. Possiamo porre perciò P A
bB ¼ x.
una volta che si conosce l’angolo PA
È importante fare alcune osservazioni circa le misure degli angoli che abbiamo annotato in figura:
bM è retto, quindi l’angolo alla circonferenza APbM, insistendo sullo stesso arco di AO
bM, è con– l’angolo al centro AO
gruente alla sua metà e misura ;
4
b
b
– P AB ffi P Q M perché angoli alterni interni rispetto alle due rette parallele AB e MQ, tagliate dalla trasversale AQ;
– poiché M PbQ ¼ 3
b Q ¼ 3 x ¼ x.
¼
, segue che PM
4
4
4
4
π
–x
4
M
t
π
4
Figura 1
A
x
r
O
x
P
r
B
Q
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
Considerare una semicirconferenza di diametro AB ¼ 2r e, indicato con M il punto medio dell’arco AB, tracciare
_
la tangente t alla semicirconferenza in M. Sull’arco BM determinare un punto P in modo che la semiretta AP inpffiffiffi
tersechi la retta t in un punto Q, distinto da M, per cui: PM 2 þ PQ ¼ kMQ. Discutere il problema rispetto al parametro k.
2/5
Problemi di trigonometria con discussione
Limiti geometrici dell’incognita
_
Al variare di P su BM , x varia evidentemente tra 0 e . Analizziamo i casi limite.
4
– Se P B, è x ¼ 0 (fig. 2) e la retta AP è parallela alla tangente t alla semicirconferenza in M, quindi non esiste Q.
– Se P M, è x ¼
(fig. 3) e la retta AP interseca la tangente in P stesso, quindi Q P M.
4
M
t
Figura 2
r
O
r
P≡M≡Q
π
4
P≡B
A
r
r
O
x=0
x=
π
4
ESERCIZI
A
t
B
Figura 3
Il testo del problema richiede che la retta AP intersechi la retta t e che il punto di intersezione sia distinto da M, condizioni
che evidentemente non sono soddisfatte in corrispondenza dei casi limite. Escludiamo perciò i casi limite e assumiamo
come domino per l’incognita x l’intervallo:
0<x<
4
Espressione dell’equazione fornita dal problema
pffiffiffi
Nelle ipotesi assunte si ha MQ 6¼ 0, quindi possiamo dividere entrambi i membri della relazione PM 2 þ PQ ¼ kMQ per
MQ, ottenendo l’equazione equivalente:
PM pffiffiffi
PQ
2þ
¼k
MQ
MQ
[1]
k= 2
Y
2 2
B , 
2 2
O
X2 + Y2 = 1
X
A
k=1
Figura 4 La retta passante per B è tangente
alla circonferenza goniometrica.
13 Considera una semicirconferenza di diametro di misura AB ¼ 2r; traccia nel semipiano, avente come origine la retta
AB, che la contiene la semiretta tangente in A alla semicirconferenza e considera su tale semiretta il punto M tale che
2
2
2
AM ¼ 4r. Determina sulla semicirconferenza
un punto P in modo che sia verificata la relazione MP ¼ AP þ kBP .
bP ¼ x si ha l’equazione 4 4 sin x cos x ¼ k sin2 x, con 0 < x ;
Ponendo BA
2
due soluzioni per 3 k 4, una soluzione per k > 4
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
Questa osservazione ci consente di scrivere facilmente l’equazione espressa dal problema in funzione di x. Infatti i rapporti che compaiono nella [1] sono rapporti tra coppie di lati del triangolo PMQ e sono quindi uguali ai rapporti tra i seni
degli angoli a essi opposti. Facendo riferimento alla fig. 1, otteniamo cosı̀ che la [1] equivale a:
x
sin
sin x pffiffiffi
4
2þ
¼k
3
3
sin
sin
4
4
ossia, svolgendo i calcoli: sin x þ cos x ¼ k.
Questa equazione va discussa rispetto alle limitazioni 0 < x < .
4
Discussione dell’equazione
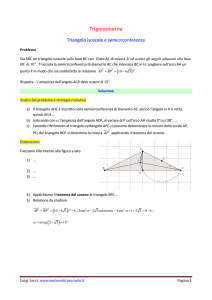
Ponendo sin x ¼ Y e cos x ¼ X ed effettuando la discussione, otteniamo la fig. 4, da cui deduciamo che il problema ampffiffiffi
mette una soluzione per 1 < k < 2.
3/5
Problemi di trigonometria con discussione
In un triangolo ABC le misure dei lati AC e CB sono rispettivamente 3 e 2 e l’angolo ACB misura . Determina sul
3
lato AC un punto P e sul lato BC un punto Q, in modo che:
14
AP ¼ BQ
e
2
2
2
2
AB þ BQ þ QP þ PA ¼ k
Ponendo AP ¼ BQ ¼ x, si ottiene l’equazione 3x2 5x þ 14 ¼ k con 0 x 2;
143
k 14 e una soluzione per 14 < k 16
due soluzioni per
12
Due semicirconferenze di diametri AB ¼ BC ¼ 2r sono tangenti esternamente nel punto B e giacciono dalla stessa
che incontrano le due semicirparte rispetto ad AC. Da B si conducono due semirette formanti fra loro un angolo di
4
conferenze, oltre che in B, rispettivamente nei punti D ed E. Determina l’angolo ABbD ¼ x in modo che sia
2
2
2
DE þ EC ¼ kBD .
Si ottiene l’equazione ð2 kÞ cos2 x sin x cos x þ 1 ¼ 0, con
< x < ; una soluzione per k > 3
4
2
15
ESERCIZI
In una circonferenza di centro O e raggio 1, la corda AB è il lato del quadrato inscritto. Condotta nel punto B la semiretta tangente alla circonferenza che giace, rispetto alla retta AB, nel semipiano che contiene il centro O, determina
sulla semiretta un punto P tale che sia verificata la relazione:
pffiffiffi
BM þ 2 2MP
¼k
PB
16
dove M è l’ulteriore punto di intersezione del segmento AP con la circonferenza.
bP ¼ x, si ottiene l’equazione 3 sin x þ cos x k ¼ 0 con 0 < x < ;
Posto BA
4
pffiffiffi
una soluzione per 1 < k < 2 2
bC ¼ . Considerata la semicirconferenza di diametro AB, esterna
Nel triangolo ABC, rettangolo in B, è AB ¼ 1 e BA
4
al triangolo, determina su di essa un punto P in modo che, condotta per P la perpendicolare ad AB fino a incontrare l’ipotenusa AC nel punto Q, risulti:
17
AQ þ QP ¼ kAB
a. la misura del lato BC e delle due parti in cui è diviso dal punto S;
b. il coseno dell’angolo in B e la misura della bisettrice AS.
2
2
2
Determina quindi un punto P, sul segmento AS, in modo che si abbia: PA þ PB þ PC ¼ k.
pffiffiffiffiffiffi
pffiffiffiffiffiffi
21
5 pffiffiffiffiffiffi
4 pffiffiffiffiffiffi
20 pffiffiffi
b
a. BC ¼ 21, BS ¼
21, CS ¼
21; b. cos ABC ¼
, AS ¼
3;
9
9
9
7
pffiffiffi
20 pffiffiffi
posto AP ¼ x si ottiene l’equazione 3x2 9 3x þ 41 k ¼ 0, con 0 x 3;
9
83
229
229
k
e una soluzione per
< k 41
due soluzioni per
4
9
3
bC ¼ e OA ¼ 1. Posto CA
bO ¼ x,
Il punto O è l’ortocentro di un triangolo acutangolo ABC del quale è noto che BA
esprimi in funzione di x e le misure dei tre lati del triangolo e quelle dei segmenti OB e OC. Supposto poi che
1
cos ¼ , determina x in modo che si abbia:
3
19
2OB þ 3OC ¼ kBC
pffiffiffi
pffiffiffi
1
Si ottiene l’equazione 7 sin x þ 4 2 cos x 2k 2 ¼ 0 con 0 < x < arccos ;
3
pffiffiffi 9 2
una soluzione per 2 < k 3 e due soluzioni per 3 < k 4
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
pffiffiffi
bP ¼ x si ha l’equazione ð1 þ 2Þ cos2 x þ sin x cos x ¼ k con 0 x ;
Posto BA
2
q
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffi
pffiffiffi
pffiffiffi
pffiffiffi
pffiffiffi
1
1þ 2þ 4þ2 2
una soluzione per 0 k < 1 þ 2, due soluzioni per 1 þ 2 k 2
18 Il triangolo ABC ha i lati AB e AC che misurano rispettivamente 5 e 4 e l’angolo fra essi compreso misura . Detta
3
AS la bisettrice interna dell’angolo di vertice A, calcola:
4/5
Problemi di trigonometria con discussione
20 Data una semicirconferenza di diametro AB e raggio 3r, considera sul diametro AB il punto D tale che AD ¼ r. Determina sulla semicirconferenza un punto C in modo che, condotta da C la tangente alla semicirconferenza, essa intersechi la parallela ad AC condotta da D in un punto E e si abbia DE ¼ kr.
bC ¼ x, si ottiene l’equazione 4 cos2 x k cos x þ 1 ¼ 0 con 0 x < ;
Ponendo BA
2
due soluzioni per 4 k 5, una soluzione per k > 5
Sia CD una corda di una semicirconferenza di centro O e diametro AB e sia E il punto in comune ai prolungamenti
7
bE in modo che sia vedelle corde AC, BD. Sapendo che il rapporto fra CD e AB è
, determina la misura x dell’angolo BA
25
rificata la relazione:
21
bE ¼ x si ottiene l’equazione 5 sin x þ 6 cos x 6k ¼ 0, con arcsin 7 x ;
Posto BA
25
2
pffiffiffiffiffiffi 5
179
179
61
e due soluzioni per
k
una soluzione per k <
6
150
150
6
ESERCIZI
AE
13 BE
þ
¼k
25 AB
AB
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
5/5