Valentina Rindinella 4H
2015/16
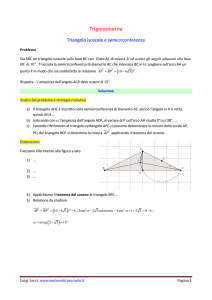
Nel triangolo ABC la misura di AC è 4 e il coseno
dell'angolo in A è ¾. Il punto D divide AB nei segmenti
AD=2 e DB=1. Trova CD, CB e la misura di CM, mediana
relativa ad AB
C
DATI
AC=4
AD=2
DB=1
cos A=3/4
α
A
DATI RICHIESTI
CD=?
CB=?
CM=?
B
M
D
Sapendo che a2=b2+c2-2bc cos α (Teorema del coseno)
Consideriamo prima il triangolo ACD e poniamo:
AC=b ; AD=c ; CD=a
a2=16+4-2(4)(2)(3/4)=8
a=2√2 quindi
C
CD=2√2
Consideriamo ora il triangolo CBA e poniamo:
AC=b ; AB=c ; CD=a
Sapendo che AB=AD+DB allora AB=3
a2=16+9-2(4)(3)(3/4)=7
A
α
a=√7 quindi CB=√7
Consideriamo infine il triangolo ACM e poniamo:
AC=b ; AM=c ; CM=a
a2=16+9/4-2(4)(3/2)(3/4)=37/4
a=√37/2 quindi CM=√37/2
M
D
B