archi speciali - maurolabarbera

FUNZIONI GONIOMETRICHE DI ARCHI SPECIALI
30° e 60°
̂ di ampiezza 𝜋 (60°) e
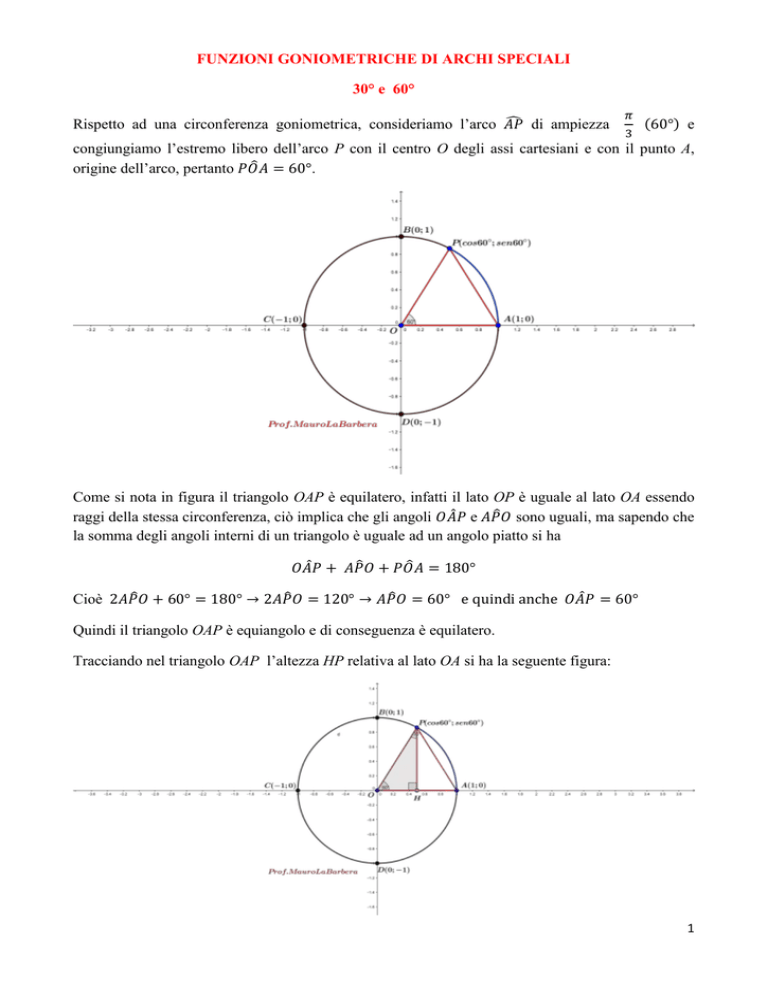
Rispetto ad una circonferenza goniometrica, consideriamo l’arco 𝐴𝑃
3
congiungiamo l’estremo libero dell’arco P con il centro O degli assi cartesiani e con il punto A,
origine dell’arco, pertanto 𝑃𝑂̂𝐴 = 60°.
Come si nota in figura il triangolo OAP è equilatero, infatti il lato OP è uguale al lato OA essendo
raggi della stessa circonferenza, ciò implica che gli angoli 𝑂𝐴̂𝑃 e 𝐴𝑃̂𝑂 sono uguali, ma sapendo che
la somma degli angoli interni di un triangolo è uguale ad un angolo piatto si ha
𝑂𝐴̂𝑃 + 𝐴𝑃̂𝑂 + 𝑃𝑂̂𝐴 = 180°
Cioè 2𝐴𝑃̂𝑂 + 60° = 180° → 2𝐴𝑃̂ 𝑂 = 120° → 𝐴𝑃̂𝑂 = 60° e quindi anche 𝑂𝐴̂𝑃 = 60°
Quindi il triangolo OAP è equiangolo e di conseguenza è equilatero.
Tracciando nel triangolo OAP l’altezza HP relativa al lato OA si ha la seguente figura:
1
e sapendo che in un triangolo equilatero l’altezza relativa ad un lato è anche mediana si ottiene
̅̅̅̅
𝑂𝐻 = ̅̅̅̅
𝐻𝐴 =
1
2
1
̅̅̅̅
𝑂𝐴 ed essendo ̅̅̅̅
𝑂𝐴 = 1 si ottiene ̅̅̅̅
𝑂𝐻 = ̅̅̅̅
𝐻𝐴 =
2
Inoltre, sapendo che in un triangolo equilatero l’altezza relativa ad un lato è anche bisettrice si ha
𝐴𝑃̂𝐻 = 𝐻𝑃̂𝑂 =
1
1
𝐴𝑃̂𝑂 = 60° = 30°
2
2
Applicando il Teorema di Pitagora al triangolo rettangolo OHP si può scrivere
̅̅̅̅2 = 𝑂𝐻
̅̅̅̅ 2 + 𝐻𝑃
̅̅̅̅ 2
𝑂𝑃
Calcolando il cateto maggiore HP si ottiene:
̅̅̅̅2 − 𝑂𝐻
̅̅̅̅ 2 = √1 −
̅̅̅̅ = √𝑂𝑃
𝐻𝑃
1
4−1
3
√3 √3
=√
=√
=
=
4
3
4
2
√4
Pertanto, per definizione di seno si ha
̅̅̅̅̅ = 𝒔𝒆𝒏 𝝅 = √𝟑 cioè 𝒔𝒆𝒏𝟔𝟎° = √𝟑
𝑯𝑷
𝟑
𝟐
𝟐
e per definizione di coseno si ha
̅̅̅̅̅ = 𝒄𝒐𝒔 𝝅 = 𝟏 cioè 𝒄𝒐𝒔𝟔𝟎° = 𝟏
𝑶𝑯
𝟑
𝟐
𝟐
Osservazione:
Analogamente si può dimostrare che
𝝅
𝟏
𝟔
𝟐
𝒔𝒆𝒏 =
e 𝒄𝒐𝒔
𝝅
𝟔
=
√𝟑
𝟐
cioè 𝒔𝒆𝒏𝟑𝟎° =
𝟏
𝟐
e 𝒄𝒐𝒔𝟑𝟎° =
√𝟑
𝟐
.
2
FUNZIONI GONIOMETRICHE DI ARCHI SPECIALI
45°
̂ di ampiezza 𝜋 (45°) e
Rispetto ad una circonferenza goniometrica, consideriamo l’arco 𝐴𝑃
4
congiungiamo l’estremo libero dell’arco P con il centro O degli assi cartesiani, inoltre sia H la
proiezione del punto P sull’asse delle ascisse, pertanto 𝑃𝑂̂𝐻 = 45°.
Come si nota in figura il triangolo OHP è rettangolo ed isoscele, infatti
̂ 𝑃 = 90° , 𝑃𝑂̂𝐻 = 𝐻𝑃̂𝑂 = 45° ,
𝑂𝐻
in virtù del Teorema di Pitagora si ha
̅̅̅̅2 = 𝑂𝐻
̅̅̅̅ 2 + 𝐻𝑃
̅̅̅̅ 2
𝑂𝑃
Ed essendo i cateti uguali, cioè ̅̅̅̅
𝐻𝑃 = ̅̅̅̅
𝑂𝐻 si può scrivere
̅̅̅̅
̅̅̅̅ 2
𝑂𝑃2 = 2𝑂𝐻
Di conseguenza sapendo che ̅̅̅̅
𝑂𝑃 = 1 poiché raggio della circonferenza si ottiene
̅̅̅̅ 2 = 1 → ̅̅̅̅
2𝑂𝐻
𝑂𝐻 2 =
1
1
1
√2
→ ̅̅̅̅
𝑂𝐻 = √ =
=
2
2 √2
2
Pertanto, per definizione di seno si ha
𝝅
√𝟐
√𝟐
̅̅̅̅̅
𝑯𝑷 = 𝒔𝒆𝒏 =
cioè 𝒔𝒆𝒏𝟒𝟓° =
𝟒
𝟐
𝟐
e per definizione di coseno si ha
̅̅̅̅̅ = 𝒄𝒐𝒔 𝝅 = √𝟐 cioè 𝒄𝒐𝒔𝟒𝟓° = √𝟐 .
𝑶𝑯
𝟒
𝟐
𝟐
3