19/12/2014
1) Due molle di costanti elastiche e lunghezza a riposo rispettivamente di K1= 10 N/m, K2=
20 N/m, l1=10 cm ed l2=20 cm, sono collegate in serie e sottoposte a trazione tramite
lʼapplicazione nel punto A di una forza F parallela alle molle. Per effetto di questa forza
la lunghezza del sistema delle due molle è L=40 cm. Calcolare la lunghezza di ciascuna
molla nella situazione di deformazione prodotta dalla forza F. Calcolare infine lʼenergia
potenziale del sistema.
2) La posizione di due particelle di massa m1=1Kg ed m2=2Kg è descritta delle equazioni
r1=3t i + 2t2 j ed r2=4t2 i + (5t+1)j. Calcolare la posizione del centro di massa del
sistema e la sua velocità allʼistante t=2s.
3) Allʼestremità di una molla di costante elastica K=400N/m viene ancorata una massa
m=2 Kg. La molla viene poi allungata lungo la direzione y e portata allʼaltezza ya=50 cm.
Il corpo in tale configurazione è soggetto alla forza peso e alla forza di richiamo della
molla. Calcolare la velocità del corpo quando, dopo esser stato rilasciato, si porta alla
quota yb=10 cm. Si supponga yeq.=0.
4) Calcolare il campo elettrico generato da una lastra piana indefinita su cui è presente
una carica positiva con densità costante σ=10-8 C/m2.
5) Due sfere di massa m1=1 kg ed m2=2 kg sono saldate agli estremi di un asta di
lunghezza 2m e massa 1kg. Lʼasta è vincolata a ruotare attorno ad un asse verticale
passante per il suo centro. Calcolare il momento dʼinerzia del sistema. Si calcoli inoltre
lʼenergia cinetica e il momento angolare L del sistema ipotizzando che questo venga
messo in rotazione con velocità angolare ω= 1 rad/s.
6) Sul bordo esterno di una piattaforma circolare di raggio R=3m, inizialmente in quiete,
cʼè un uomo fermo. La piattaforma è vincolata a ruotare intorno al suo centro e ha
momento dʼinerzia I=1800 kgm2. Lʼuomo comincia a correre con velocità tangenziale
v=4.2 m/s, rispetto allʼambiente esterno. Calcolare la velocità angolare della
piattaforma, lʼenergia cinetica dellʼuomo e della piattaforma e il lavoro compiuto
dallʼuomo. Si consideri la massa dellʼuomo uguale a 60 Kg.
7) Un blocco scorrevole di massa M=3.3 Kg è appoggiato ad una superficie orizzontale
priva di attrito e legato, con una fune che passa su una puleggia priva di massa e attrito,
ad un secondo blocco appeso di massa m=2.1 Kg. Mentre il blocco appeso cade, quello
scorrevole verrà accelerato. Trovare lʼaccelerazione del blocco scorrevole,
lʼaccelerazione del blocco appeso, la tensione della corda.
8)Un satellite per le telecomunicazioni si muove su un orbita geostazionaria, cioè un
orbita circolare situata nel piano equatoriale, alla stessa velocità angolare di
rotazione della terra, in modo che le antenne paraboliche al suolo che ricevono i
segnali provenienti dal satellite possano essere orientate in una direzione fissa. Si
calcoli il raggio dellʼorbita geostazionaria e la velocità periferica rispetto ad un
sistema di riferimento inerziale avente origine nel centro della terra. La massa della
terra è MT=5.97 1024 Kg.
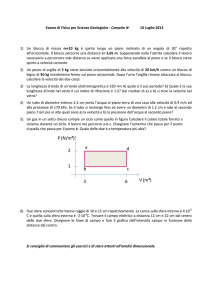
9) Una massa m, si trova su un piano orizzontale liscio ed è attaccata a due molle di
costanti elastiche K1 e K2 come in figura. La massa viene spostata di una quantità x
rispetto alla posizione in cui è in quiete ed entrambe le molle sono in condizioni di
riposo. Determinare il moto della massa. Si consideri K1= 10N/m, K1= 20N/m ed m=2 kg.