Esercizio: calcolo dei valori di
probabilità del valor medio di
n = 10 lanci di dado
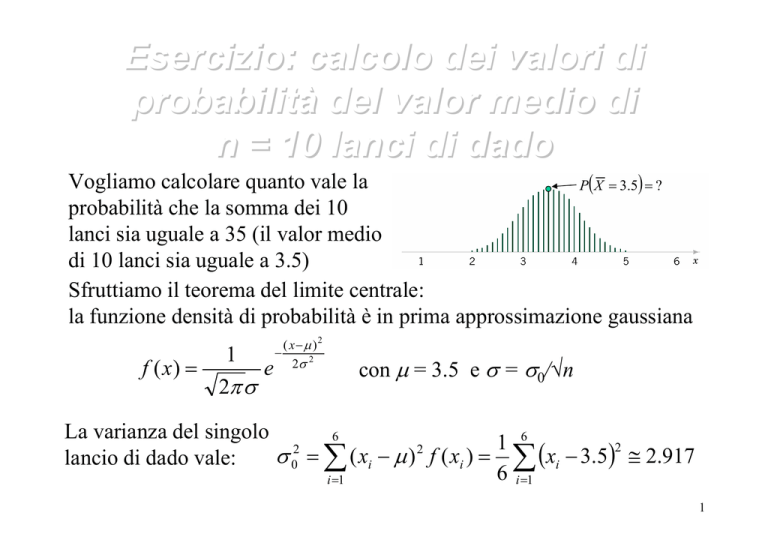
Vogliamo calcolare quanto vale la
P (X = 3.5) = ?
probabilità che la somma dei 10
lanci sia uguale a 35 (il valor medio
di 10 lanci sia uguale a 3.5)
Sfruttiamo il teorema del limite centrale:
la funzione densità di probabilità è in prima approssimazione gaussiana
f ( x) =
1
e
2π σ
−
( x−µ )2
2σ 2
con µ = 3.5 e σ = σ0/√n
La varianza del singolo
6
6
1
2
2
2
(
)
σ
=
x
−
µ
f
x
=
x
−
3
.
5
≅ 2.917
(
)
(
)
lancio di dado vale:
∑
∑
0
i
i
i
6 i =1
i =1
1
Esercizio: calcolo dei valori di
probabilità del valor medio di
n = 10 lanci di dado
Lo scarto quadratico medio del
P (X = 3.5) = ?
valor medio dopo 10 tiri vale:
σ 02
2.917
σ=
≅
≅ 0.540
10
10
Per calcolare la probabilità di avere 3.5 è necessario integrare la densità
di probabilità. In prima approssimazione l’integrale vale f(x) calcolata
nel punto per il passo di discretizzazione ∆x=1/n=0.1
f (3.5) =
1
e
2π σ
−
( 3.5 − µ ) 2
2σ 2
=
1
≅ 0.739
2π 0.54
La probabilità di fare 35 come somma di 10 lanci di dado
vale quindi: f(3.5)·0.1 ≅ 0.074
2












