RELAZIONE DI LABORATORIO
Esercitazione di laboratorio di Elettrotecnica N° 1
Svolta in data 12/10/2010
Corso di laurea in Ingegneria Aerospaziale
Docente del corso ZICH RICCARDO
Squadra (A,B,C) B
Tavolo N° 4
Componenti:
COGNOME
NOME
MATRICOLA
Capocchiano
Carlo
744790
Chiementin
Luca
742073
Chow
Alex Nicolas
743474
Pag. 1 di 7
MISURAZIONE DELLE RESISTENZE
1. OBIETTIVI
Verificare il valore della resistenza di #2 resistori e la coerenza dei dati ottenuti sperimentalmente con i
valori ricavati attraverso la lettura del codice colore.
2. DESCRIZIONE DELL’ESPERIMENTO E SCHEMA CIRCUITALE
Lettura del codice colore riportato su i due elementi.
Costruzione del circuito composto dal resistore in esame collegato tramite due cavi ad un
multimetro, settato come ohmmetro.
Successiva lettura della resistenza equivalente dei resistori connessi in parallelo ed in serie.
Tabulazione dei dati ottenuti.
3. STRUMENTI E MATERIALI UTILIZZATI
#2 resistori (di resistenza incognita).
Il resistore ideale è un componente passivo che, se attraversato da corrente, causa una caduta di tensione ai
suoi capi. Quelli utilizzati sono lineari e rispondono quindi alla legge di Ohm.
Basetta millefori.
Consente di effettuare i collegamenti. E’ realizzata in modo tale che due elementi circuitali i cui estremi
siano posizionati sulla medesima riga vengano messi in contatto da una lamina metallica interna.
Multimetro Agilent 34401A.
Un multimetro è uno strumento che, come dice il nome, permette la misurazione di diverse grandezze
fisiche. In questo esperimento sarà utilizzato come ohmmetro (la funzione è evidenziata nel cerchio rosso).
Lo strumento genera una ddp e misura una corrente: attraverso la legge di Ohm ottiene la resistenza. Il valore
è automaticamente visualizzato sullo schermo dello strumento con opportuna unità di misura e prefissi che
permettono di riportare con brevità valori con ordini di grandezza molto diversi tra loro.
Cavi di collegamento, di colori rosso e nero.
Un cavo ideale è un corto circuito, di conseguenza ha una resistenza nulla.
Nei calcoli seguenti, tutti gli elementi circuitali sono considerati ideali.
Pag. 2 di 7
4. RISULTATI ATTESI (TEORICI)
Il codice colore è una convenzione che permette l’immediata lettura del valore di una resistenza. Consiste in
quattro o cinque bande colorate disposte sequenzialmente lungo l’asse del resistore stesso. Le prime tre o
quattro bande indicano il valore nominale della resistenza. L’ultima indica la tolleranza che il valore reale
deve rispettare.
Nel nostro caso:
Resistenza 1
Colore
Significato[Ω]
Resistenza 2
Colore
Significato[Ω]
Marrone
1
Rosso
2
Nero
0
Nero
0
Arancione
000
Arancione
000
Oro
±5%
Oro
±5%
Teoricamente otteniamo che la resistenza equivalente risulta:
Parallelo
Req
R1 R2
R1 R2
6.667 kΩ
Serie
Req
R1 R2
30 kΩ
5. RISULTATI SPERIMENTALI
I risultati ottenuti sperimentalmente sono riassunti nella tabella seguente:
Resistenza 1
Resistenza 2
Parallelo
Serie
Valore Atteso [kΩ]
10
20
6.667
30
Valore Misurato [kΩ]
9.945
19.789
6.619
29.734
Errore ε%
-0.55%
-1.06%
-0.72%
-0.89%
6. CONCLUSIONI
Nel procedere della misura si è reso necessario pressare i terminali metallici dei cavi sulle estremità
del resistore utilizzando le dita. Lasciandolo semplicemente appoggiato sulle punte metalliche la misura
risulta estremamente imprecisa poiché qualunque perturbazione esterna, ad esempio vibrazioni, causa un
errore di misura che non permette di ottenere un valore attendibile, in quanto in ogni istante il multimetro
legge valori molto diversi tra loro.
Questo modo di procedere causa tuttavia un errore, seppur ben più modesto, dovuto al contatto con
le dita stesse che collegano il corpo (che ha resistenza dell’ordine del MΩ) in parallelo con gli elementi in
esame: il multimetro “vede” una resistenza inferiore.
Per evitare questo problema si è agito fissando, in un secondo momento, i resistori su una basetta
millefori e pressando sopra i terminali. Si è evitato così il contatto con le dita.
L’errore calcolato con questo modo di procedere risulta del tutto accettabile, non solo rientra pienamente nel
range di tolleranza dichiarato dal costruttore (5%) ma è ≤1%: possiamo quindi affermare di avere ottenuto
una misura ragionevolmente precisa.
Pag. 3 di 7
PARTITORE RESISTIVO DI TENSIONE IN C.C.
1. OBIETTIVI
Verificare sperimentalmente la Legge di Kirchhoff delle Tensioni (KVL) attraverso il partitore di tensione.
2. DESCRIZIONE DELL’ESPERIMENTO E SCHEMA CIRCUITALE
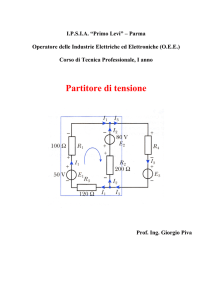
Si è costruito il circuito posizionando i resistori in serie sulla basetta millefori (come in figura).
Le resistenze sono state connesse al generatore tramite due morsetti a coccodrillo.
Il generatore è stato impostato a 5 V.
È stata misurata la tensione a vuoto e assunta come potenziale teorico Eth.
Infine, per effettuare la misura, i morsetti collegati al multimetro, sono stati posizionati, in due fasi
successive, in parallelo alle resistenze, così da rilevare la caduta di tensione su R1 e R2.
Come controprova è stata misurata la caduta di potenziale su R1 + R2.
3. STRUMENTI E MATERIALI UTILIZZATI
#2 resistori (di resistenza 10 kΩ e 20 kΩ).
Basetta millefori.
Multimetro Agilent 34401A.
Il settaggio in modalità voltmetro è illustrato nella figura seguente.
Generatore di tensione Stab AR140.
Il generatore di tensione ideale è un elemento
circuitale che impone una differenza di
potenziale costante tra due punti, qualunque sia
la corrente che lo attraversa.
Cavi di collegamento, di colori
rosso e nero.
(Riferimenti teorici al secondo esperimento)
Pag. 4 di 7
4. RISULTATI ATTESI (TEORICI)
La tensione a vuoto misurata è Eth = 5.155V.
La formula utilizzata per calcolare V1 e V2 è il partitore di tensione.
Il valore di E è calcolato utilizzando la KVL (come controprova, risulta uguale a Eth).
Resistenza 1
V1
Eth
Resistenza 2
V2
Eth
R1
R1
1.718 V
R2
R2
R1
3.437 V
R2
E V1 V2
E
5.155 V
5. RISULTATI SPERIMENTALI
I risultati ottenuti sperimentalmente sono riassunti nella tabella seguente:
V1
V2
E
Valore Atteso [V]
1.718
3.437
5.155
Valore Misurato [V]
1.723
3.429
5.155
Errore ε%
0.29%
-0.23%
0.00%
Come controprova, abbiamo calcolato la somma tra V1 e V2 (ad ulteriore verifica della KVL risulta
uguale al valore di E):
V1 + V2
5.155
5.152
-0.06%
6. CONCLUSIONI
La Legge di Kirchhoff delle Tensioni afferma che il potenziale elettrico è funzione solo della
posizione e non dipende quindi dal percorso seguito. Di conseguenza lungo un circuito chiuso, la sommatoria
di tutte le tensioni è pari a 0V.
Per i calcoli teorici sono stati
utilizzati i valori nominali dei resistori:
l’errore percentuale ottenuto risulta
imputabile unicamente ad un valore
errato della resistenza inserita nelle
formule teoriche. Utilizzando infatti i
valori misurati al primo esperimento
l’errore si riduce allo 0%. Ovviamente i
valori misurati con il multimetro
risentono dell’errore strumentale di
quest’ultimo, che non possiamo né
correggere né stimare.
Come controprova abbiamo
sommato i valori di V1 e V2: possiamo
vedere che questo valore si discosta di
solo lo 0.06% da E, a riconferma della
validità di quanto esposto. Si sottolinea
il fatto che la caduta di potenziale su un resistore è proporzionale al valore della resistenza stessa, come ci si
attende dalla formula del partitore e che la tensione misurata a vuoto risulta uguale (seppur fino alla terza
cifra decimale) alla caduta di tensione misurata sulle due resistenze in serie.
Pag. 5 di 7
PARTITORE RESISTIVO DI CORRENTE IN C.C.
1. OBIETTIVI
Verificare sperimentalmente la Legge di Kirchhoff delle correnti (KCL) attraverso il partitore di corrente.
2. DECRIZIONE DELL’ESPERIMENTO E SCHEMA CIRCUITALE
Si è costruito il circuito posizionando i resistori in parallelo sulla basetta millefori (come in figura).
Le resistenze sono state connesse al generatore tramite due morsetti a coccodrillo.
Il generatore è stato impostato a 5.1 V.
Per effettuare la misura, il multimetro, è stato posizionato, in due fasi successive, in serie ad ogni
resistenza, così da rilevare la corrente passante per le singole R1 e R2. Per collegare in parallelo le
due resistenze, i loro estremi vanno allacciati sulla stessa fila della basetta. Per aggiungere in serie ad
una singola resistenza l’amperometro, un estremo del resistore prescelto si inserisce in una diversa
riga della basetta e tra le due resistenze così posizionate viene inserito l’amperometro.
Sono state misurate la corrente erogata I e la tensione imposta Eth.
3. STRUMENTI E MATERIALI UTILIZZATI
#2 resistori (di resistenza 10 kΩ e 20 kΩ).
Basetta millefori.
Multimetro Agilent 34401A.
Il settaggio in modalità amperometro è illustrato nella figura seguente:
Generatore di tensione Stab AR140.
Cavi di collegamento, di colori rosso e nero.
(Riferimenti teorici al secondo esperimento)
Pag. 6 di 7
4. RISULTATI ATTESI (TEORICI)
La tensione a vuoto misurata è Eth = 5.430 V. La resistenza equivalente (calcolata a pag. 3) è Req = 6.667 kΩ.
La formula utilizzata per calcolare I1 e I2 è il partitore di corrente.
I th
Ith
Resistenza 1
I1
I th
Resistenza 2
I2
I th
Eth
Req
0.815 mA
R2
R1
R2
R1
R1
R2
0.543 mA
0.272 mA
5. RISULTATI SPERIMENTALI
I risultati ottenuti sperimentalmente sono riassunti nella tabella seguente:
I1
I2
I
Valore Atteso [mA]
0.543
0.272
0.815
Valore Misurato [mA]
0.546
0.274
0.820
Errore ε%
0.55%
0.74%
0.68%
6. CONCLUSIONI
La Legge di Kirchhoff delle Correnti afferma che la sommatoria delle correnti entranti ed uscenti da
una superficie chiusa è pari a 0A. Nel caso particolare di un nodo, le correnti entranti sono uguali alle
correnti uscenti. Per verificare
tale legge abbiamo utilizzato il
partitore di corrente, verificando
che i valori misurati siano
coerenti con le correnti calcolate.
In effetti i valori misurati si
discostano di meno dell’1%
rispetto ai dati teorici.
Ciononostante l’errore è
maggiore di quello ottenuto nel
secondo esperimento poiché la Ith
è stata calcolata tramite la Req
teorica, che differisce da quella
reale per lo 0,72% (pag. 3).
Come già detto per il secondo
esperimento, è l’utilizzo dei
valori ideali delle resistenze a
causare gli errori sopra elencati:
utilizzando infatti i valori
sperimentali l’errore si riduce
allo 0%.
È infine interessante notare che, come ci si aspetta dalla formula del partitore, la corrente passante
per un ramo del parallelo è direttamente proporzionale alla resistenza presente sul ramo opposto.
Pag. 7 di 7