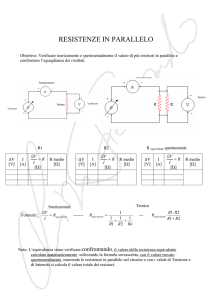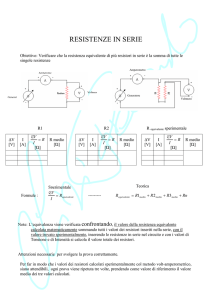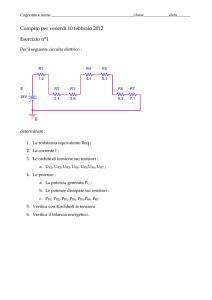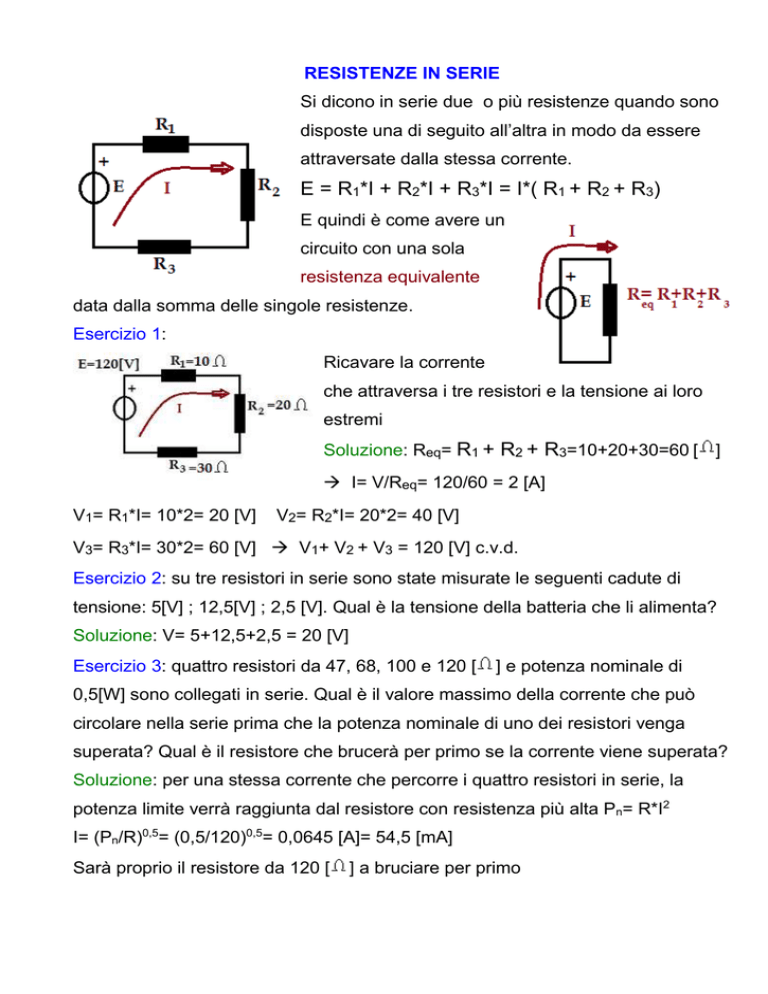
RESISTENZE IN SERIE
Si dicono in serie due o più resistenze quando sono
disposte una di seguito all’altra in modo da essere
attraversate dalla stessa corrente.
E = R1*I + R2*I + R3*I = I*( R1 + R2 + R3)
E quindi è come avere un
circuito con una sola
resistenza equivalente
data dalla somma delle singole resistenze.
Esercizio 1:
Ricavare la corrente
che attraversa i tre resistori e la tensione ai loro
estremi
Soluzione: Req= R1 + R2 + R3=10+20+30=60 [ ]
I= V/Req= 120/60 = 2 [A]
V1= R1*I= 10*2= 20 [V]
V2= R2*I= 20*2= 40 [V]
V3= R3*I= 30*2= 60 [V] V1+ V2 + V3 = 120 [V] c.v.d.
Esercizio 2: su tre resistori in serie sono state misurate le seguenti cadute di
tensione: 5[V] ; 12,5[V] ; 2,5 [V]. Qual è la tensione della batteria che li alimenta?
Soluzione: V= 5+12,5+2,5 = 20 [V]
Esercizio 3: quattro resistori da 47, 68, 100 e 120 [
] e potenza nominale di
0,5[W] sono collegati in serie. Qual è il valore massimo della corrente che può
circolare nella serie prima che la potenza nominale di uno dei resistori venga
superata? Qual è il resistore che brucerà per primo se la corrente viene superata?
Soluzione: per una stessa corrente che percorre i quattro resistori in serie, la
potenza limite verrà raggiunta dal resistore con resistenza più alta Pn= R*I2
I= (Pn/R)0,5= (0,5/120)0,5= 0,0645 [A]= 54,5 [mA]
Sarà proprio il resistore da 120 [
] a bruciare per primo
RESISTENZE IN PARALLELO
Due o più resistenze si dicono collegate in
parallelo quando hanno la stessa d.d.p. ai loro
capi.
I= I1+ I2+ I3= E/R1+ E/R2+ E/R3
=E*(1/R1+1/R2+1/R3) E= Req*I da cui risulta:
La resistenza equivalente di più resistori in parallelo è
pari al reciproco della somma dei reciproci delle singole
resistenze.
Esercizio: calcolare E, I1, I2, I3, P1,P2,P3, Ptot
Soluzione: Req= 18,18 [
]
E= Req*I= 18,18*2= 36,36 [V]
I1= E/R1= 0,727 [A]
I2= E/R2= 0,363 [A]
I3= E/R3= 0,909 [A]
P1= V*I1= 26,4 [W]
P2= V*I2=13,2 [W]
P3= V*I3= 33 [W]
Ptot= P1+ P2+ P3= 72,7 [W] che è anche uguale a E*I= 36,36*2 c.v.d.