1
Congruenza diretta e inversa
PROPRIETÀ. La congruenza tra due figure piane mantiene inalterata la lunghezza dei segmenti e
l’ampiezza degli angoli; ciò che cambia è la posizione delle figure nel piano.
DEFINIZIONE. Si chiamano movimenti rigidi quelle trasformazioni geometriche che mantengono
inalterate forma ed estensione. Possiamo distinguerli in:
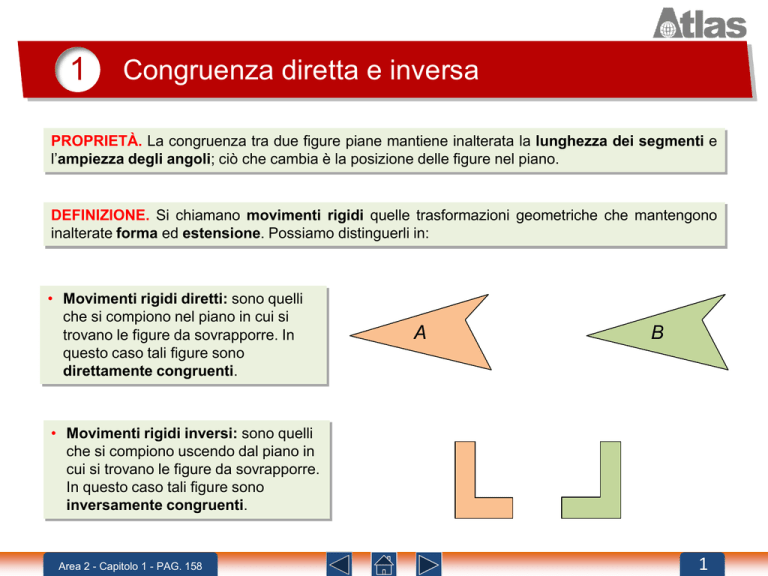
• Movimenti rigidi diretti: sono quelli
che si compiono nel piano in cui si
trovano le figure da sovrapporre. In
questo caso tali figure sono
direttamente congruenti.
A
B
• Movimenti rigidi inversi: sono quelli
che si compiono uscendo dal piano in
cui si trovano le figure da sovrapporre.
In questo caso tali figure sono
inversamente congruenti.
Area 2 - Capitolo 1 - PAG. 158
1
2
La traslazione
Consideriamo il triangolo rettangolo ABC e
spostiamolo nel piano in modo tale che i
segmenti che uniscono A con A’, B con B’ e C
con C’ siano paralleli tra loro e tali da avere:
la stessa lunghezza, che prende il nome di
modulo;
la stessa direzione, quella della retta a cui
appartengono;
lo stesso verso di percorrenza, in questo
caso da sinistra verso destra, come indicato
dalla freccia.
DEFINIZIONE. La traslazione è un movimento isometrico diretto del piano determinato da un
vettore che fissa modulo, direzione e verso di spostamento.
PROPRIETÀ. La traslazione è una trasformazione geometrica che conserva la misura delle
lunghezze e l’ampiezza degli angoli; due figure ottenute mediante una traslazione sono direttamente
congruenti.
Area 2 - Capitolo 1 - PAG. 159
2
3
La rotazione
La rotazione è un movimento rigido che
permette di ruotare una figura attorno a un
punto, detto centro di rotazione, di un angolo
con ampiezza assegnata.
La rotazione può essere oraria o antioraria.
DEFINIZIONE. La rotazione è un movimento isometrico diretto del piano determinato da un centro
di rotazione e da un angolo orientato che definisce l’ampiezza e il verso del movimento nel piano.
PROPRIETÀ. La rotazione è una trasformazione geometrica che conserva la misura delle
lunghezze e l’ampiezza degli angoli; due figure ottenute mediante una rotazione sono direttamente
congruenti.
Area 2 - Capitolo 1 - PAG. 161
3
4
La simmetria assiale
DEFINIZIONE. La simmetria assiale di asse a è un
movimento isometrico del piano ed è tale da associare ad ogni
punto del piano un punto simmetrico rispetto alla retta a.
PROPRIETÀ. La simmetria assiale è una trasformazione
geometrica che conserva la misura delle lunghezze e
l’ampiezza degli angoli; due figure ottenute tramite una
simmetria assiale sono inversamente congruenti.
DEFINIZIONE. Tutti i punti della figura che appartengono
contemporaneamente anche all’asse si chiamano punti uniti.
PROPRIETÀ. Una figura possiede un asse di simmetria se
esiste una retta tale che è possibile associare a ciascun punto
della figura un altro punto anch’esso appartenente alla figura.
Area 2 - Capitolo 1 - PAG. 163
4
5
La simmetria centrale
DEFINIZIONE. La simmetria centrale di centro O è un
movimento isometrico diretto del piano ed è tale da associare ad
ogni punto del piano un punto simmetrico rispetto al centro O.
PROPRIETÀ. Due punti qualunque A e A’ si corrispondono in
una simmetria centrale di centro O se O è il punto medio del
segmento AA’.
PROPRIETÀ. La simmetria centrale è una trasformazione
geometrica che conserva le misure delle lunghezze e l’ampiezza
degli angoli; due figure ottenute tramite una simmetria centrale
sono direttamente congruenti.
PROPRIETÀ. Una figura possiede un centro di simmetria se
esiste un punto tale che è possibile associare a ciascun punto
della figura un altro punto anch’esso appartenente alla figura.
Area 2 - Capitolo 1 - PAG. 164
5
6
La simmetria e i poligoni
Bisettrice di un angolo
La bisettrice dell’angolo è l’asse di simmetria dell’angolo.
Tutti i punti della bisettrice r e il vertice V sono punti uniti.
Triangolo isoscele
In un triangolo isoscele la bisettrice, l’altezza, l’asse e la
mediana, rispetto alla base, coincidono nello stesso segmento.
La retta r che contiene tale segmento rappresenta l’asse di
simmetria del triangolo.
Tutti i punti notevoli del triangolo e gli altri punti del segmento
CH sono punti uniti.
Area 2 - Capitolo 1 - PAG. 167
6
6
La simmetria e i poligoni
Triangolo equilatero
In un triangolo equilatero la bisettrice, l’altezza, la mediana e
l’asse di ciascun lato coincidono nello stesso segmento. Le rette
r1, r2, r3, che contengono tali segmenti sono tre assi di simmetria
del triangolo equilatero.
Parallelogrammo
Il punto O d’incontro delle due diagonali è il centro di simmetria
del parallelogrammo. In generale il parallelogrammo non ha assi
di simmetria.
Area 2 - Capitolo 1 - PAG. 167
7
6
La simmetria e i poligoni
Rettangolo
Le due rette r1 e r2, perpendicolari nei punti medi della base e
dell’altezza, sono assi di simmetria. Il punto O, intersezione
delle rette r1 e r2, rappresenta il centro di simmetria del
rettangolo.
Quadrato
Le quattro rette r1, r2, perpendicolari nei punti medi dei lati, e r3 e
r4, contenenti le diagonali BD e AC, sono gli assi di simmetria
del quadrato. Il punto O, comune alle quattro rette, è il centro di
simmetria del quadrato.
Area 2 - Capitolo 1 - PAG. 167
8
6
La simmetria e i poligoni
Rombo
Le due rette r1 e r2 contenenti le diagonali sono assi di
simmetria del rombo. I punti del segmento AC sono punti uniti
all’asse r2, i punti dell’asse BD sono punti uniti dell’asse r1. Il
punto O, intersezione delle due diagonali, è il centro di
simmetria del rombo.
Trapezio isoscele
La retta r perpendicolare alle due basi e passante per il loro
punto medio è l’asse di simmetria del trapezio.
Area 2 - Capitolo 1 - PAG. 168
9
6
La simmetria e i poligoni
Poligoni regolari
Le sei rette della figura a lato rappresentano altrettanti assi di
simmetria. In generale, un poligono regolare ha tanti assi di
simmetria quanti sono i suoi lati. Tutti i poligoni con un numero
pari di lati hanno anche un centro di simmetria; quelli con un
numero dispari di lati non possiedono centro di simmetria.
Circonferenza e cerchio
Qualunque retta passante per il centro della circonferenza
rappresenta un asse di simmetria. La circonferenza e il cerchio
possiedono quindi infiniti assi di simmetria. Il centro O della
circonferenza è il centro di simmetria.
Area 2 - Capitolo 1 - PAG. 168
10