Isometrie: trasformazioni geometriche di figure nel piano che

LE ISOMETRIE
Isometria: trasformazione
geometrica di figure nel piano
che mantiene la lunghezza dei
segmenti e l’ampiezza degli
angoli ma cambia la posizione
della figura.



Traslazione
Rotazione
Simmetria:
- Centrale
- Assiale
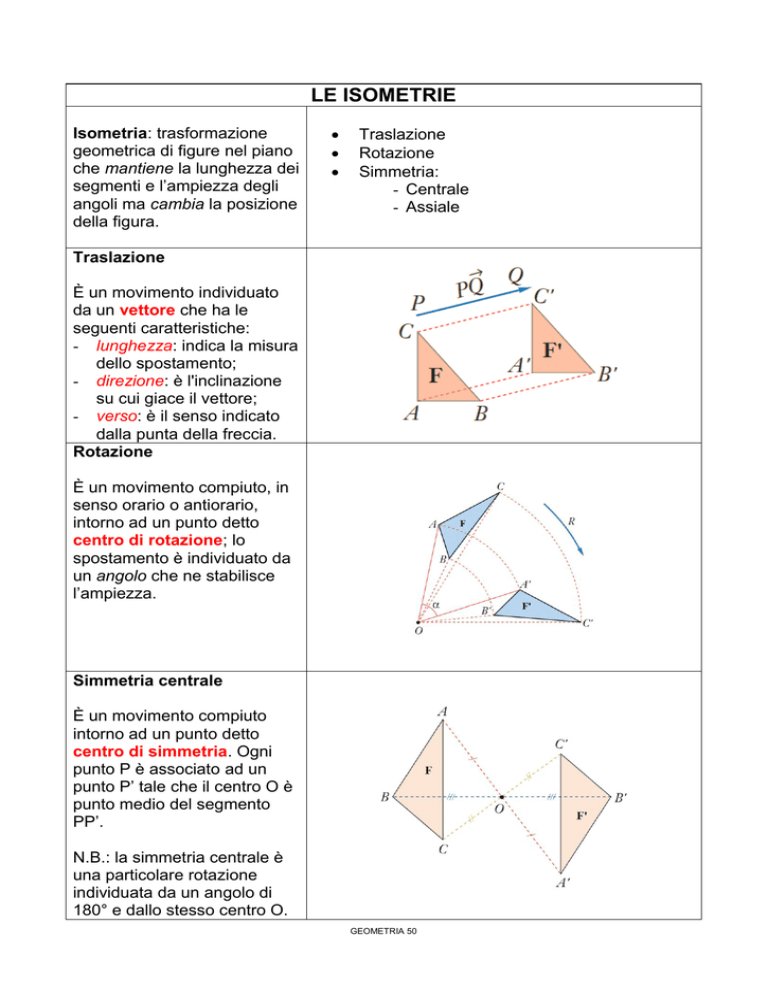
Traslazione
È un movimento individuato
da un vettore che ha le
seguenti caratteristiche:
- lunghezza: indica la misura
dello spostamento;
- direzione: è l'inclinazione
su cui giace il vettore;
- verso: è il senso indicato
dalla punta della freccia.
Rotazione
È un movimento compiuto, in
senso orario o antiorario,
intorno ad un punto detto
centro di rotazione; lo
spostamento è individuato da
un angolo che ne stabilisce
l’ampiezza.
Simmetria centrale
È un movimento compiuto
intorno ad un punto detto
centro di simmetria. Ogni
punto P è associato ad un
punto P’ tale che il centro O è
punto medio del segmento
PP’.
N.B.: la simmetria centrale è
una particolare rotazione
individuata da un angolo di
180° e dallo stesso centro O.
GEOMETRIA 50
Simmetria assiale
È
una
trasformazione
isometrica individuata da una
retta detta asse di simmetria.
Ogni punto P è associato ad
un punto P’ equidistante
dall’asse di simmetria. P e P’
sono
su
una
retta
perpendicolare all’asse di
simmetria.
Ad un poligono è possibile
applicare consecutivamente
due o più isometrie.
Simmetria e poligoni
Alcune figure possiedono uno
o più assi di simmetria:
un asse: triangolo isoscele,
trapezio isoscele
due assi: rettangolo, rombo
I poligoni regolari hanno tanti
assi di simmetria quanti sono i
loro lati.
Il cerchio ha infiniti assi di
Esempi di assi di simmetria nelle figure piane.
simmetria: qualsiasi retta
passante per il suo centro.
GEOMETRIA 51
Isometrie: esercizi guidati
Quale trasformazione geometria fa
corrispondere:
 la figura F alla figura F’?
…………………………………
.
 la figura F’ alla figura F’’?
………………………………....
.
 la figura F alla figura F’’?
…………………………………
.
Come sono tra loro gli assi r ed s?
………………………………………..
La
composizione
di
due
simmetrie……………………………
ad
assi
…………………..
corrisponde ad una
…………………………………….. o
....................................................
Quale trasformazione geometrica fa
corrispondere:
 la figura F alla figura F’?
………………………………….
 la figura F’ alla figura F’’?
…………………………………
 la figura F alla figura F’’?
…………………………………
Come sono tra loro gli assi r ed t?
…………………………………………
La composizione di due simmetrie
………………………………………….
ad
assi
…………………..
corrisponde
ad
una
………………………………..
GEOMETRIA 52
Stabilisci quali tra le seguenti coppie
di figure sono state ottenute
mediante una simmetria assiale
quindi tracciane l’asse si simmetria.
Disegna sul piano cartesiano il
poligono di vertici A(1;1), B(5;1) e
C(2;4).
Applica ad esso una simmetria
centrale avente centro in O(5;4).
Utilizzando le regole della simmetria
centrale è stato disegna il punto C’
tale che CO = OC’.
Traccia ora i punti B’ e A’ poi unisci
A’ B’ C’.
Osserva i disegni, la retta tracciata è
l'asse di simmetria della figura?
GEOMETRIA 53