INTEGRALI
1. Integrali indefiniti
Sia f(x) una funzione continua in [a, b]. Una funzione F(x) definita e continua in [a, b],
derivabile in ]a, b[, dicesi primitiva di f(x) in [a, b] se F’(x) = f(x), ∀ x ∈ ]a, b[.
Teoremi
1. Se F(x) è una primitiva di f(x) in [a, b] allora anche G(x) = F(x) + k, con k ∈ R, è una primitiva
di f(x) in [a, b]
Infatti, basta osservare che G(x) è una funzione definita e continua in [a, b], derivabile in ]a, b[ e
che G’(x) = [ F(x) + k ]’ = F’(x) = f(x), ∀ x ∈ ]a, b[.
2. Se F(x) e G(x) sono due primitive qualsiasi di f(x) in [a, b] allora esse differiscono per una
costante, cioè esiste una costante k ∈ R tale che risulti G(x) = F(x) + k, ∀ x ∈ [a, b].
Infatti posto H(x) = G(x) – F(x) si ha H’(x) = [G(x) –F(x)]’ = G’(x) – F’(x) = f(x) – f(x) = 0, ∀x ∈
]a b[. Per un corollario del teorema di Lagrange segue che H(x) e’ costante in [a, b], cioè esiste una
costante k ∈ R tale che H(x) = G(x) – F(x) = k, ossia G(x) = F(x) +k
Dicesi integrale indefinito di f(x) in [a, b] l’insieme di tutte le sue primitive in [a, b] e si indica col
simbolo
∫ f ( x)dx
.
L’integrazione, in simboli
∫ f ( x)dx , è l’operazione inversa della derivazione.
Un importante teorema ci assicura che ogni funzione continua è integrabile, cioè possiede una
primitiva, tuttavia la determinazione di una primitiva di una funzione composta non sempre risulta
agevole.
Dalla “tabella delle derivate” e dalla regola di derivazione di una funzione composta segue
facilmente:
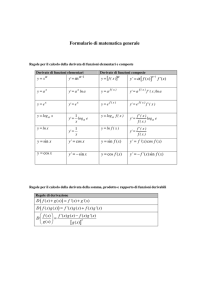
∫ dx = x + k
x α +1
∫ x dx = α + 1 + k
a
(α ≠ −1)
- Integrali -
1
1
∫ x dx = log x + k
∫ cos xdx = senx + k
∫ senxdx = − cos x + k
1
∫ cos
2
dx = tgx + k
x
1
∫ sen
2
dx = − cot gx + k
x
x
∫ a dx =
∫e
x
dx = e x + k
1
∫
ax
+k
log a
1− x2
1
∫1+ x
2
dx = arcsenx + k
dx = arctgx + k
∫ cos f ( x) ⋅ f ' ( x)dx = senf ( x) + k
∫ senf ( x) ⋅ f ' ( x)dx = − cos f ( x) + k
f ' ( x)
dx = tgf ( x) + k
2
f ( x)
∫ cos
f ' ( x)
dx = − cot gf ( x) + k
2
f ( x)
∫ sen
f (x)
∫a
∫e
∫
f (x)
f (x)
a
⋅ f ' ( x)dx =
+k
log a
⋅ f ' ( x)dx = e f ( x ) + k
f ' ( x)
1 − f 2 ( x)
dx = arcsenf ( x) + k
f ' ( x)
dx = arctgf ( x) + k
2
( x)
∫1+ f
f
a +1
( x)
+k
α +1
∫
f α ( x) ⋅ f ' ( x)dx =
∫
f ' ( x)
dx = log f ( x) + k
f ( x)
(α ≠ −1 )
- Integrali -
2
2. Regole di integrazione
•
Dalla regola di derivazione della somma (differenza) di due funzioni segue:
∫ ( f ( x) ± g ( x))dx = ∫ f ( x)dx ± ∫ g ( x)dx
•
Dalla regola di derivazione del prodotto di una costante per una funzione segue:
∫ k ⋅ f ( x)dx = k ∫ f ( x)dx
•
Dalla regola di derivazione del prodotto di due funzioni, avendosi:
D[u(x)⋅v(x)] = u’(x)⋅v(x) + u(x)⋅v’(x),
ossia
u’(x)⋅v(x) = D[u(x)⋅v(x)] – u(x)⋅v’(x)
segue
ossia
∫ u' ( x) ⋅ v( x)dx = ∫ D[u ( x) ⋅ v( x)]dx − ∫ u ( x) ⋅ v' ( x)dx
(*) ∫ u ' ( x) ⋅ v( x)dx = u ( x) ⋅ v( x) − ∫ u ( x) ⋅ v' ( x)dx
Posto u’(x) = h(x) la (*) diventa:
(**) ∫ h( x) ⋅ v( x)dx = P[h( x)] ⋅ v( x) − ∫ P[h( x) ⋅ v' ( x)dx
essendo P[h(x)] una primitiva di h(x).
La (*) ovvero la (**) dicesi regola di integrazione per parti. Essa risulta particolarmente utile
quando si debba calcolare l’integrale del prodotto di due funzioni. Poiché nel secondo
membro della (**) compaiono la derivata di una delle due funzioni e una primitiva
dell’altra e’ chiaro che nell’applicare tale regola conviene scegliere come funzione h(x)
quella di cui si conosce già una primitiva e per v(x) quella funzione la cui derivata abbia
un espressione più’ semplice di v(x).
- Integrali -
3
Esempi:
•
∫ xe
x
dx
v( x) = x
poniamo
x
u ' ( x) = h( x) = e
∫ xe
•
x
x
dx = e x x − ∫ e x dx = e x − e x + C
∫ x sen xdx
v( x) = x
poniamo
u ' ( x) = h( x) = sen x
∫ x sen xdx = − x cos x − ∫ − cos xdx = − x cos x + sen x + C
•
∫ cos
2
dx
v( x) = cos x
poniamo
u ' ( x) = h( x) = cos x
∫ cos
2
xdx = ∫ cos x cos xdx = sen x cos x − ∫ − sen 2 xdx = sen x cos x + ∫ (1 − cos 2 x)dx =
= sen x cos x + ∫ dx − ∫ cos 2 xdx = sen x cos x + x + C − ∫ cos 2 xdx
es sen do
∫ cos
2
2
xdx = sen x cos x + x + C − ∫ cos 2 xdx segue
2∫ cos xdx = sex cos x + x + C
∫ cos
2
xdx =
ossia
1
(sen x cos x + x ) + C
2
- Integrali -
4
3. Integrali definiti
Ancora da inserire
Vedi testi suggeriti
- Integrali -
5
4. Regole e proprietà’ degli integrali definiti
•
Teorema fondamentale del calcolo integrale:
Se f(x) è una funzione continua e ≥ 0, l’area A del sottografico di f(x) nell’intervallo [a, b]
(trapezoide) è data da:
b
A = ∫ f ( x)dx = [F ( x)]a = F (b) − F (a)
b
a
b
dove il simbolo
∫
f ( x ) dx è detto integrale definito della funzione f(x) nell’intervallo [a, b] e
a
F(x) è una qualsiasi primitiva di f(x).
•
Nel caso in cui f(x) è una funzione continua e nell’intervallo [a, b] risulta essere f(x) ≤ 0,
cioè il suo grafico in detto intervallo sta nel semipiano negativo delle y, l’area del
sottografico di f(x) relativo all’intervallo [a, b] è data da:
b
A = − ∫ f ( x)dx = −[F ( x)]a = F (a) − F (b)
b
a
(basti pensare che in tal caso sarà –f(x) ≥ 0 e che i sottografici di f(x) e –f(x) nell’intervallo
[a, b] hanno la stessa area).
•
Se y = f(x) e y = g(x) sono due funzioni tali che in tutti i punti dell’intervallo [a, b] è g(x)
≤ f(x) (anche se g(x) è in parte ≤ 0) l’area della regione piana delimitata superiormente
dal grafico di y = f(x) e inferiormente dal grafico di y = g(x) e dalle rette x = a e x = b è
data dalla formula:
b
A = ∫ ( f ( x) − g ( x) )dx = [F ( x) − G ( x)]a
b
a
essendo F(x) e G(x) due qualsiasi primitive rispettivamente di f(x) e di g(x).
y
y =f(x)
a
b
x
y = g(x)
- Integrali -
6
•
E’ possibile spezzare l’intervallo di integrazione in due o più parti. Più precisamente se
c è un punto interno ad [a, b] è
b
∫
a
c
b
a
c
f ( x)dx = ∫ f ( x)dx + ∫ f ( x)dx
Esempio:
x2 − 4
per
x ≤ −2 ∪ x ≥ 2
4 − x2
per − 2 < x < 2
7
dovendosi calcolare
∫x
2
− 4 dx , poiché è x 2 − 4 =
−1
si ha:
2
7
x3
x3
x
−
4
dx
=
(
4
−
x
)
dx
+
(
x
−
4
)
dx
=
4
x
−
+
− 4 x = ............
∫−1
∫−1
∫2
3 −1 3
2
7
2
7
2
2
2
Si osservi che tale proprietà è utile quando è necessario calcolare integrali del tipo
b
∫ f ( x)dx
con f(x) discontinua in un numero finito di punti interni all’intervallo [a, b]. Se ad
a
esempio c e d, con c < d, sono punti di discontinuità della f(x) all’interno di [a, b] viene
spontaneo porre:
b
∫
a
c
d
b
a
c
d
f ( x)dx = ∫ f ( x)dx + ∫ f ( x)dx + ∫ f ( x)dx
E’ chiaro che gli integrali a secondo membro esistono purché f(x) possieda limite sinistro e
limite destro finiti in ciascuno dei suoi punti di discontinuità’.
•
Chiaramente se la funzione f(x) è simmetrica rispetto all’origine, cioè f(x) è una
a
funzione dispari, si ha:
∫ f ( x)dx = 0
−a
2 x4
44
4 4
2
2
Esempio: ∫ (2 x − x )dx = x − = 4 −
− (− 4) − − = 0
4
4
−4
4
−4
4
4
3
- Integrali -
7
•
Volume di un solido di rotazione.
Facendo ruotare attorno all’asse x il grafico di f(x) nell’intervallo [a, b], si ottiene un solido
di rotazione il cui volume è:
b
V = π ∫ f 2 ( x)dx
a
Esempio. La funzione y = r 2 − x 2 , definita nell’intervallo [-r, r] ruotando attorno all’asse
x genera la sfera di centro l’origine e raggio r e il suo volume è:
r
V =π ∫
−r
(r
2
−x
2
) dx = π ∫ (
2
r
−r
x3
r3
r 3 4
r − x dx = π r 2 x − = π r 3 − − − r 3 + = πr 3
3 −r
3
3 3
2
2
r
)
Integrali generalizzati.
La nozione di integrale definito può essere estesa ai casi di intervalli non limitati del tipo
[a, +∞), illimitato a destra, oppure (-∞, a], illimitato a sinistra, o infine (-∞, +∞), illimitato
da entrambi i lati.
Si parla allora di integrali generalizzati.
Per definizione è:
+∞
b
∫ f ( x)dx = lim ∫ f ( x)dx
b → +∞
a
b
∫
−∞
a
b
f ( x)dx = lim ∫ f ( x)dx
a → −∞
a
ovviamente tali definizioni hanno senso solo quando il limite a secondo membro esiste
finito.
Nel caso di integrale esteso ad un intervallo illimitato da entrambi i lati (-∞, +∞) basta
spezzarlo negli intervalli (-∞, c], [c, +∞) con c un arbitrario punto dell’asse reale per
ricondursi ai due casi precedenti.
E’ dunque
+∞
c
b
∫ f ( x)dx = lim ∫ f ( x)dx + lim ∫ f ( x)dx
−∞
a → −∞
a
b → +∞
c
- Integrali -
8
Esempi.
0
•
∫e
x
dx esiste
−∞
0
poichè è
•
+∞
1
∫ x dx
[ ]
lim ∫ e x dx = lim e x
a → −∞
a → −∞
a
0
a
= lim (1 − e a ) = 1
a → −∞
invece non esiste
1
b
poichè è
lim
b → +∞
∫ x dx = lim [log x]
1
1
b → +∞
b
1
= lim log b = +∞
b → +∞
- Integrali -
9