Approssimazione della distribuzione binomiale alla

Approfondimento 3.3
Approssimazione della distribuzione binomiale alla normale
Come aveva notato de Moivre, se il numero di prove è sufficientemente ampio e la probabilità del
successo π sufficientemente maggiore di zero − anche se nessuno, poi, ha mai specificato cosa
intende per “numero di prove sufficientemente ampio” (alcuni riferiscono maggiore di 5, altri di 10,
altri ancora di 30…) e “probabilità di successo π sufficientemente maggiore di zero” − la
distribuzione binomiale può essere approssimata alla normale. Solani (2008) suggerisce che questa
operazione è possibile date le seguenti condizioni:
• Se π < ,05 o π ≥ ,95 e n ≥ 100
• Se ,05 ≤ π < ,10 o ,90 ≤ π < ,95 e n ≥ 50
• Se ,10 ≤ π < ,90 e n ≥ 20
mentre Borra e Di Ciaccio (2008) indicano che la numerosità può considerarsi adeguata quando n ×
π ≥ 5 e n × (1 − π) ≥ 5.
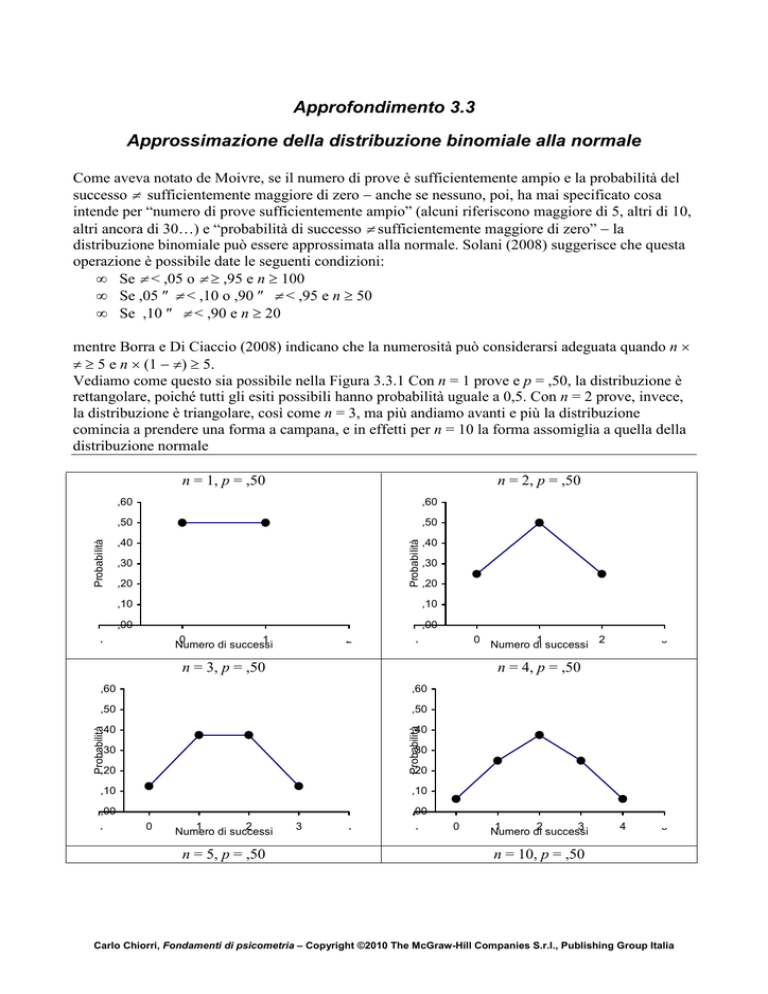
Vediamo come questo sia possibile nella Figura 3.3.1 Con n = 1 prove e p = ,50, la distribuzione è
rettangolare, poiché tutti gli esiti possibili hanno probabilità uguale a 0,5. Con n = 2 prove, invece,
la distribuzione è triangolare, così come n = 3, ma più andiamo avanti e più la distribuzione
comincia a prendere una forma a campana, e in effetti per n = 10 la forma assomiglia a quella della
distribuzione normale
n = 2, p = ,50
,60
,60
,50
,50
,40
,40
Probabilità
Probabilità
n = 1, p = ,50
,30
,20
,10
,30
,20
,10
,00
,00
-1
0
1
Numero
di successi
2
-1
0 Numero di1 successi 2
n = 3, p = ,50
n = 4, p = ,50
,50
,50
,40
,40
,20
Probabilità
,60
Probabilità
,60
,10
,10
,30
,00
-1
3
,30
,20
0
1 di successi
2
Numero
n = 5, p = ,50
3
4
,00
-1
0
1
3
Numero
di2 successi
4
5
n = 10, p = ,50
Carlo Chiorri, Fondamenti di psicometria – Copyright ©2010 The McGraw-Hill Companies S.r.l., Publishing Group Italia
,60
,50
,50
,40
,40
Probabilità
Probabilità
,60
,30
,30
,20
,20
,10
,10
,00
-1
,00
-1
0
1 Numero
2 di successi
3
4
5
6
0
1
2
3
4
5
6
7
8
9 10 11
Numero di successi
n = 20, p = ,50
n = 30, p = ,50
,30
,20
,15
Probabilità
Probabilità
,20
,10
,10
,05
,00
-1 0 1 2 3 4 5 6
7 8 9 10111213141516171819202122
Numero
di successi
,00
Numero di successi
-1 0 1 2 3 4 5 6 7 8 9 1011121314151617181920212223242526272829303132
Figura 3.3.1 Approssimazioni successive della distribuzione binomiale alla normale per p = ,50
L’approssimazione alla normale della distribuzione binomiale vale anche per probabilità di
successo diverse da ,50, e quindi distribuzioni binomiali asimmetriche. In questo caso, però, la
distribuzione binomiale ha bisogno di un numero maggiore di prove per approssimarsi
adeguatamente alla normale. La Figura 3.3.2 e 3.3.3 mostrano i casi di p = ,33 e p =,10
n = 1, p = ,33
n = 2, p = ,33
,70
,50
,40
Probabilità
Probabilità
,50
,30
,10
,20
,10
,00
-,10
-1
,30
0
1
Numero di successi
n = 3, p = ,33
2
-1
0 Numero di1 successi 2
3
n = 4, p = ,33
Carlo Chiorri, Fondamenti di psicometria – Copyright ©2010 The McGraw-Hill Companies S.r.l., Publishing Group Italia
,50
,50
,40
,40
,20
Probabilità
,60
Probabilità
,60
,10
,10
,30
,30
,20
,00
-1
0
1 di successi
2
Numero
3
4
,00
-1
0
1
3
Numero
di2 successi
5
n = 10, p = ,33
,60
,50
,50
,40
,40
,30
,30
,20
,20
,10
,10
,00
-1
,00
-1
Probabilità
,60
Probabilità
n = 5, p = ,33
4
0
1 Numero
2 di successi
3
4
5
6
n = 20, p = ,33
0
1
2 Numero
3 4 di5 successi
6 7 8
9 10 11
n = 30, p = ,33
,30
,20
,15
Probabilità
Probabilità
,20
,10
,10
,05
,00
-1 0 1 2 3 4 5 6
7 8 9 10111213141516171819202122
Numero
di successi
,00
Numero di successi
-1 0 1 2 3 4 5 6 7 8 9 1011121314151617181920212223242526272829303132
Figura 3.3.2 Approssimazioni successive della distribuzione binomiale alla normale per p = ,33
n = 2, p = ,10
1,00
1,00
,80
,80
Probabilità
Probabilità
n = 1, p = ,10
,60
,40
,40
,20
,20
,00
,00
-1
,60
0
1
Numero di successi
n = 3, p = ,10
2
-1
0 Numero di1 successi 2
3
n = 4, p = ,10
Carlo Chiorri, Fondamenti di psicometria – Copyright ©2010 The McGraw-Hill Companies S.r.l., Publishing Group Italia
,80
,80
Probabilità
1,00
Probabilità
1,00
,60
,60
,40
,40
,20
,20
,00
-1
0
1 di successi
2
Numero
3
4
,00
-1
0
n = 5, p = ,10
1
3
Numero
di2 successi
4
5
n = 10, p = ,10
1,00
,60
,80
,50
Probabilità
Probabilità
,40
,60
,30
,40
,20
,20
,10
,00
-1
,00
-1
0
1Numero
2 di successi
3
4
5
6
n = 20, p = ,10
,30
0
1
2 Numero
3 4 di5 successi
6 7 8
9 10 11
n = 30, p = ,10
,30
,25
,20
Probabilità
Probabilità
,20
,15
,10
,10
,05
,00
-1 0 1 2 3 4 5 6
7 8 9 10111213141516171819202122
Numero
di successi
,00
Numero di successi
-1 0 1 2 3 4 5 6 7 8 9 1011121314151617181920212223242526272829303132
Figura 3.3.3 Approssimazioni successive della distribuzione binomiale alla normale per p = ,10
Supponiamo quindi che ci venga chiesto di determinare quale è la probabilità di ottenere, con una
moneta onesta, un numero di teste compreso fra 233 e 260 su 500 lanci. Naturalmente potremmo
 500  233 500−233
,50 ,50
,
munirci di (molta) pazienza e metterci a calcolare tutti i vari p(233) = 
 233
 500  234 500−234
 500  235 500−235
,50 ,50
,50 ,50
p(234) = 
, p(235) = 
,…,
 234 
 235 
 500  2600 500−260
,50 ,50
p(260) = 
, e sommare tutti i risultati, ma comprendente bene che, a meno di
 260 
farlo fare al computer, è un’impresa improba. Possiamo però sfruttare l’approssimazione della
normale alla binomiale, e considerare l’intervallo 233-260 come un intervallo di classe i cui limiti
reali siano 232,5 e 260,5. Questa operazione si chiama correzione di continuità, perché non
dimenticate che stiamo approssimando ad una distribuzione continua una distribuzione che per sua
natura è invece discreta. A questo punto dobbiamo trasformare in punti z i valori 233,5 e 260,5. La
Carlo Chiorri, Fondamenti di psicometria – Copyright ©2010 The McGraw-Hill Companies S.r.l., Publishing Group Italia
distribuzione binomiale ha media µ = n × p e deviazione standard σ = n × p × q = n × p × (1 − p) ,
per cui, visto che stiamo considerando il caso di n = 500 lanci, avremo che µ = 500 × 0,50 = 250 e σ
= 500×,50×,50 = 11,18. Per cui i punti z corrispondenti sono:
232,5 − 250
104 − 100
z1 =
= −1,56
z2 =
= 0,94
11,18
15
A questo punto il procedimento è identico a quello già visto nel caso della distribuzione normale
standardizzata. Dobbiamo calcolare la somma delle due aree della Figura 3.3.4
Figura 3.3.4 Area di probabilità compresa fra 233 e 260 successi
Le aree si ricavano dalla tavola dei punti z (Figura 3.3.5):
Figura 3.3.5 Valori di probabilità per punteggi z compresi fra la media e -1,56 e fra la media e 0,94
Carlo Chiorri, Fondamenti di psicometria – Copyright ©2010 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Poiché i due valori di area sono ,4406 e ,3264, la soluzione è:
p(233 < successi < 260) → p(-1,56 < z < 0,94) = p(-1,56 < z < 0) + p(0 < z < 0,94) = ,4406 + ,3264
= ,7670
La probabilità di estrarre un punteggio ottenere un numero di teste compreso fra 233 e 260 con una
moneta onesta è dunque del 76,70%. Se avessimo calcolato tutte le probabilità esatte con le formule
viste nel paragrafo 2.1 di questo capitolo il risultato sarebbe stato 76,75%.
Carlo Chiorri, Fondamenti di psicometria – Copyright ©2010 The McGraw-Hill Companies S.r.l., Publishing Group Italia