AENTULA SERIE HR 15
HR 30 -15
HR 20 -15
Producibilità Energetica: aspetti teorici e valori di riferimento
Densità di probabilità [(m/s)-1]
Distribuzione di Weibull
con diversi valori del fattore di scala A
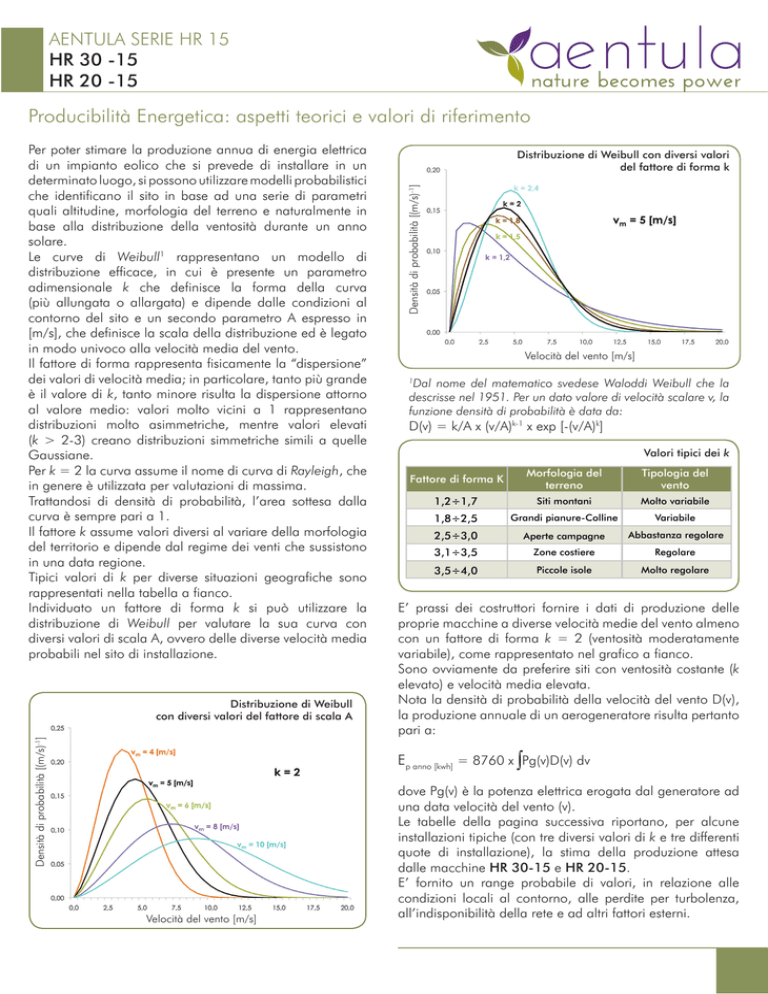
Distribuzione di Weibull con diversi valori
del fattore di forma k
Densità di probabilità [(m/s)-1]
Per poter stimare la produzione annua di energia elettrica
di un impianto eolico che si prevede di installare in un
determinato luogo, si possono utilizzare modelli probabilistici
che identificano il sito in base ad una serie di parametri
quali altitudine, morfologia del terreno e naturalmente in
base alla distribuzione della ventosità durante un anno
solare.
Le curve di Weibull1 rappresentano un modello di
distribuzione efficace, in cui è presente un parametro
adimensionale k che definisce la forma della curva
(più allungata o allargata) e dipende dalle condizioni al
contorno del sito e un secondo parametro A espresso in
[m/s], che definisce la scala della distribuzione ed è legato
in modo univoco alla velocità media del vento.
Il fattore di forma rappresenta fisicamente la “dispersione”
dei valori di velocità media; in particolare, tanto più grande
è il valore di k, tanto minore risulta la dispersione attorno
al valore medio: valori molto vicini a 1 rappresentano
distribuzioni molto asimmetriche, mentre valori elevati
(k > 2-3) creano distribuzioni simmetriche simili a quelle
Gaussiane.
Per k = 2 la curva assume il nome di curva di Rayleigh, che
in genere è utilizzata per valutazioni di massima.
Trattandosi di densità di probabilità, l’area sottesa dalla
curva è sempre pari a 1.
Il fattore k assume valori diversi al variare della morfologia
del territorio e dipende dal regime dei venti che sussistono
in una data regione.
Tipici valori di k per diverse situazioni geografiche sono
rappresentati nella tabella a fianco.
Individuato un fattore di forma k si può utilizzare la
distribuzione di Weibull per valutare la sua curva con
diversi valori di scala A, ovvero delle diverse velocità media
probabili nel sito di installazione.
Velocità del vento [m/s]
Dal nome del matematico svedese Waloddi Weibull che la
descrisse nel 1951. Per un dato valore di velocità scalare v, la
funzione densità di probabilità è data da:
1
D(v) = k/A x (v/A)k-1 x exp [-(v/A)k]
Valori tipici dei k
Fattore di forma K
Morfologia del
terreno
Tipologia del
vento
1,2÷1,7
Siti montani
Molto variabile
1,8÷2,5
Grandi pianure-Colline
Variabile
2,5÷3,0
Aperte campagne
Abbastanza regolare
3,1÷3,5
Zone costiere
Regolare
3,5÷4,0
Piccole isole
Molto regolare
E’ prassi dei costruttori fornire i dati di produzione delle
proprie macchine a diverse velocità medie del vento almeno
con un fattore di forma k = 2 (ventosità moderatamente
variabile), come rappresentato nel grafico a fianco.
Sono ovviamente da preferire siti con ventosità costante (k
elevato) e velocità media elevata.
Nota la densità di probabilità della velocità del vento D(v),
la produzione annuale di un aerogeneratore risulta pertanto
pari a:
Ep anno [kwh] = 8760 x !Pg(v)D(v) dv
Velocità del vento [m/s]
dove Pg(v) è la potenza elettrica erogata dal generatore ad
una data velocità del vento (v).
Le tabelle della pagina successiva riportano, per alcune
installazioni tipiche (con tre diversi valori di k e tre differenti
quote di installazione), la stima della produzione attesa
dalle macchine HR 30-15 e HR 20-15.
E’ fornito un range probabile di valori, in relazione alle
condizioni locali al contorno, alle perdite per turbolenza,
all’indisponibilità della rete e ad altri fattori esterni.
* Range di valori probabili in relazione alle condizioni locali al contorno (alberi, edifici, morfologia del terreno), a perdite per turbolenza, indisponibilità della rete e altri fattori esterni.
AENTULA SERIE HR 15
HR 30 -15
Stima della produzione annua di energia elettrica per installazioni tipiche*
HR 20 -15