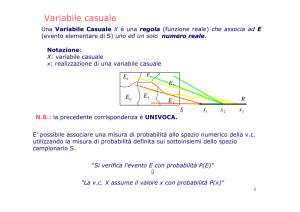
LE VARIABILI CASUALI CONTINUE
La variabile casuale è continua se assume un
qualsiasi valore nell’ambito di uno specifico
intervallo. Ad esempio altezza delle piante, diametro
di un albero, tempo di reazione nella frenata.
La variabile casuale si indica con le lettere latine
maiuscole.
LE VARIABILI CASUALI CONTINUE
FUNZIONE DI DENSITA'
Data una variabile casuale continua X si chiama
funzione di densità e si indica con f(x) una funzione
che permette di determinarne la probabilità.
LA VARIABILE CASUALE NORMALE
Per determinare la probabilità che una variabile
casuale continua assuma valori in un determinato
intervallo è spesso indispensabile conoscere la
funzione di densità ad essa associata.
La ricerca ha permesso di sapere che molti fenomeni
naturali si distribuiscono secondo una normale.
Esempi:
Diametro di una mela, altezza di una pianta, altezza
degli individui, errore di misurazione ecc.
Funzione di densità Normale
X ≈ N (µ ;σ )
2
f ( x) =
1
σ 2π
e
(
x − µ )2
−
2σ 2
µ ∈ R, σ ∈ R
+
µ : media
σ : var ianza
2
Funzione di densità Normale
Media = 0 e Varianza = 1
µ = 0
σ =1
2
La funzione di densità Normale varia al variare della media e
della varianza.
Ci sono infinite funzioni densità Normale.
µ = 0
σ =1
2
µ = 0
σ 2 = 16
µ = 10
σ 2 = 25
µ = 20
σ 2 = 25
La probabilità che una variabile casuale normale assuma
valori in un determinato intervallo si può calcolare:
1.attraverso il computer richiamando la funzione di densità
normale con quella specifica media e varianza
2.attraverso la funzione di densità normale standardizzata
che ha la media nulla e la varianza unitaria.
1. attraverso il computer richiamando la funzione di densità
normale con quella specifica media e varianza
ESEMPIO: da indagini precedentemente condotte è noto che
l’altezza dei diciottenni trentini si distribuisce
secondo una normale con media pari a 170 cm e
varianza pari a 100 cm2 .
Viene estratto un diciottenne
trentino. Qual è la probabilità che
abbia un’altezza compresa fra
180 e 200 cm?
La probabilità di osservare un valore
compreso fra 180 e 200 e' uguale a
0.157305355899827
Viene estratto un diciottenne trentino e viene misurata la
sua altezza. Qual è la probabilità che non superi i 180 cm?
La probabilità di osservare un
valore non superiore a 180 e'
uguale a 0.841344746068543
2. attraverso la funzione di densità normale standardizzata
che ha la media nulla e la varianza unitaria.
Se una variabile casuale si distribuisce secondo una
normale con una determinata media e una determinata
varianza: X ≈ N ( µ ; σ 2 )
Allora si può dimostrare che la variabile casuale trasformata:
X −µ
σ
si distribuisce secondo la normale come media nulla e
varianza unitaria:
X −µ
σ
≈ N (0;1)
La trasformazione avvenuta si chiama standardizzazione e
si indica con Z
STANDARDIZZAZIONE
X ≈ N (µ ;σ )
2
Z=
X −µ
σ
Z ≈ N (0;1)
STANDARDIZZAZIONE
Per determinare la probabilità che una variabile casuale
normale assuma valori in un determinato intervallo sono
state predisposte delle tavole che forniscono la probabilità di
una variabile casuale normale standardizzata.
Per fare ciò è necessario standardizzare la variabile casuale
normale:
Utilizzo di una tavola
Per calcolare la probabilità relativa alla variabile casuale
normale standardizzata si può utilizzare una tavola che
fornisce la probabilità che tale variabile assuma valore
compreso fra 0 e un determinato numero reale a
P (0 < Z < a )
P (0 < Z < 1.96) = 0.4750
P ( −1.96 < Z < 0) = ?
P ( −1.96 < Z < 0) =
= P (0 < Z < 1.96) = 0.475
P ( −1.96 < Z < 1.96) = ?
P (−1.96 < Z < 1.96) =
= 2 * P (0 < Z < 1.96) =
= 2 * 0.4750 = 0.95
P ( Z < 1.96) = ?
P (Z < 1.96) =
= P (∞ < Z < 1) + P (0 < Z < 1.96) =
= 0.5 + 0.4750 = 0.9750
ESEMPIO: da indagini precedentemente condotte è noto che
l’altezza dei diciottenni trentini si distribuisce
secondo una normale con media pari a 170 cm e
varianza pari a 100 cm2 .
X ≈ N (170;100)
P (180 < X < 200) = .......
STANDARDIZZAZIONE
X ≈ N (µ ;σ )
2
Z=
X −µ
σ
Z ≈ N (0;1)
X ≈ N (170;100)
P (180 < X < 200) = .......
X − 170
Z=
10
180 − 170 X − 170 200 − 170
P
<
<
= ......
10
10
10
P (1 < Z < 3) = ......
Z ≈ N (0;1)
P (1 < Z < 3) =
= P (0 < Z < 3) − P (0 < Z < 1) =
= 0.4987 − 0.3413 = 0.1574