Variabile casuale

Variabile casuale
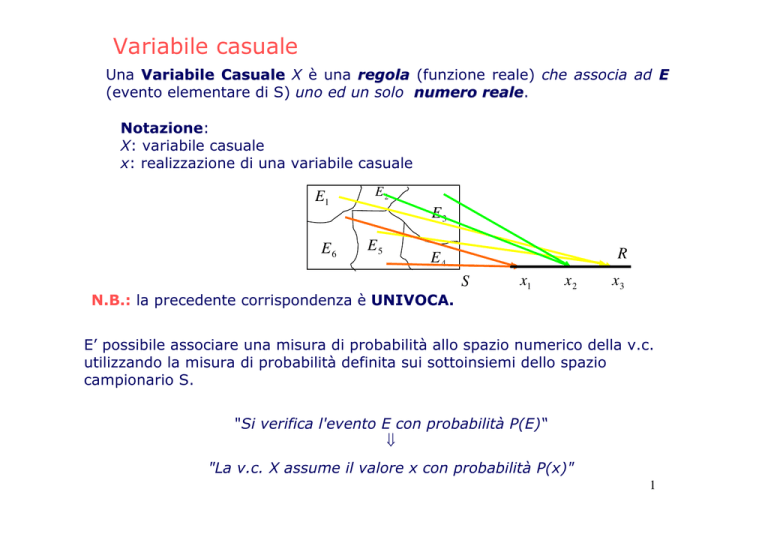
Una Variabile Casuale X è una regola (funzione reale) che associa ad E
(evento elementare di S) uno ed un solo numero reale.
reale
Notazione:
X: variabile casuale
x: realizzazione di una variabile casuale
E1
E2
E3
E6
E5
R
E4
S
x1
x2
x3
N.B.: la precedente corrispondenza è UNIVOCA.
E’ possibile associare una misura di probabilità allo spazio numerico della v.c.
utilizzando la misura di probabilità definita sui sottoinsiemi dello spazio
campionario S.
"Si verifica l'evento E con probabilità P(E)“
⇓
"La v.c. X assume il valore x con probabilità P(x)"
1
Una v.c. X è una variabile che assume valori nello spazio dei numeri reali
secondo una funzione di probabilità P(X).
1
P[X(E)]
S
E
X(E)
0
ℜ
Rappresentazione grafica dello schema
di costruzione di una v.c. discreta
1
E
1
E
6
E
E
p3
2
5
E
E
p2
3
R
4
S
x1
x2
x3
p1
0
2
Una Variabile Casuale è nota se è nota la sua distribuzione di probabilità
ESEMPI
1. Consideriamo una famiglia con 3 figli
E1
E2
E3
E4
E5
E6
E7
E8
Ω = {MMM, MMF, MFM, FMM, MFF, FMF, FFM, FFF}
P=
1/8
1/8
1/8
1/8
1/8
1/8
1/8
1/8
Variabile casuale X=“numero dei figli maschi”
{E8 }
{E5
{E2
∪ E6 ∪ E7 }
∪ E3 ∪ E 4 }
{E1 }
X
0
1
2
3
pi
1/8
3/8
3/8
1/8
xi
P(xi)
0
0,125
1
0,375
2
0,375
3
0,125
1
3
VARIABILI CASUALI DISCRETE
Assumono valori discreti (solitamente sono ottenute come risultato di
un conteggio).
Per ogni realizzazione xi risulta:
pi ≥ 0


∀i = 1, ,k
∑ pi
=1
pi
x1
x2
pi = p(xi) = probabilità che
X assuma il valore xi
x3
xi
Momenti della variabile casuale:
∑ xipi
2
Var ( X) = ∑ xi − E ( X)  pi
E (X) =
4
Esempio: lancio simultaneo di 2 monete.
Eventi elementari di Ω:
E1=TT
E2=TC
E3=CT
E4=CC
Variabile casuale “X=numero di croci”
Ei
TT
TC
CT
CC
xi
0
1
1
2
pi
1/4
1/4
1/4
1/4
Ad ogni xi associamo una probabilità pari alla somma delle probabilità
degli eventi corrispondenti.
xi
pi
0
1/4
1
2/4
2
1/4
Le xi sono le realizzazione della v.c., mentre le pi identificano la
distribuzione di probabilità della v.c. in questione
5
VARIABILI CASUALI CONTINUE
Ammettono infiniti valori, quindi non è possibile attribuire le singole
probabilità ad ogni realizzazione xi.
Si associa ad ogni intervallo una funzione f(x) detta funzione di
densità di probabilità.
N.B.:
f(x) NON è la probabilità che
X assuma il valore x!
f(x)
x
f(x) è la probabilità che X sia compresa in un
intervallo infinitesimale dx intorno ad x.
f ( x ) = p ( x − dx ≤ X ≤ x + dx )
Densità di frequenza ↔ Densità di probabilità
FUNZIONE DI DENSITÀ DI PROBABILITÀ
La funzione di densità f(x) è nulla per quei valori compresi in
esterni al campo di definizione
intervalli
Condizioni necessarie affinché una funzione di densità f(x) sia ben definita
(ossia individui una v.c.) sono:
f ( x ) ≥ 0

 +∞
 ∫ f ( x ) dx = 1
 −∞
Momenti della variabile casuale:
+∞
E (X) = µ =
∫
xf ( x )dx
−∞
2
Var ( X ) = σ2 = E ( x − µ )
7
FUNZIONE DI RIPARTIZIONE
Il passaggio dallo spazio degli eventi allo spazio dei numeri reali R
permette di ragionare in termini della relazione di ordine in R.
Considerando le realizzazioni della v.c. si può pensare alla
probabilità che X assuma valori al massimo uguali ad un x0:
∑
pi
v.c. discrete
xi ≤ x0
F (x 0 ) = P (X ≤ x 0 ) =
x0
∫ f ( x )dx
v.c. continue
−∞
Proprietà di F(x):
1) è non decrescente:
∀ x i < x j ⇒ F (x i ) ≤ F (x j )
2) 0 ≤ F(x) ≤ 1
3) lim F ( x ) = 0
x →−∞
e
lim F ( x ) = 1
x →+∞
8
VARIABILI CASUALI DISCRETE
Funzione di (distribuzione di) probabilità
pi
P (xi ) = P (X = x i )
Funzione di ripartizione
F (x 0 ) = P (X ≤ x 0 ) =
∑
x0
x1
x0
x1
xi
pi
xi ≤ x 0
Proprietà di F(x):
1) è non decrescente:
2) 0
1
≤ F(x) ≤ 1
3) lim F ( x ) = 0
x →−∞
F(x)
e
lim F ( x ) = 1
x→+∞
F(x1)
F(x0)
9
x
ESEMPIO
X: “Punteggio ottenuto nel lancio di un dado”
Funzione (o distribuzione) di probabilità
X
P(x)
1
2
3
4
5
6
1/6
1/6
1/6
1/6
1/6
1/6
pi
1/6
1
2
3
4
5
6
xi
Funzione di ripartizione
F(x)
1
∑
F ( x0 ) = P ( X ≤ x0 ) =
5/6
p ( xi )
xi ≤ x0
4/6
3/6
F (4) = P (X ≤ 4) =
2/6
1/6
∑ p ( xi ) =
xi ≤ 4
1
2
3
4
5
6
x
=
1
6
+
1
6
+
1
6
+
1
6
=
4
6
= 0, 67
VARIABILI CASUALI CONTINUE
F ( x1 ) =
x1
∫
F ( x)
f(x)dx
1
F ( x1)
F ( x0 )
−∞
Proprietà di F(x):
1) è non decrescente:
2) 0
≤ F(x) ≤ 1
3) lim F ( x ) = 0
x →−∞
e
x 0 x1
lim F ( x ) = 1
x
x→+∞
x0
F (x 0 ) =
∫
f ( x )d x
−∞
⇔
d
dx
F(x ) = f(x )
F (x 0 ) = P (X ≤ x 0 ) =
x0
∫ f ( x )dx
−∞
x0
11
PROBABILITÀ IN UN INTERVALLO CONTINUO
x0
x1
P ( x 0 ≤ X ≤ x1 ) = P ( X ≤ x1 ) − P ( X ≤ x 0 ) = F ( x1 ) − F ( x 0 ) =
x1
∫
f(x)dx
x0
x0
P (X > x0 ) = 1 − P (X ≤ x0 ) = 1 − F (x 0 ) = 1 −
x0
∫
−∞
f(x)dx
12
Alcuni schemi teorici per il calcolo della probabilità di
fenomeni reali
Per attribuire delle probabilità ad una variabile statistica (fenomeno reale) è
necessario ricondurla ad uno schema teorico, ossia inquadrare i possibili
valori che essa può assumere come possibili risultati di un esperimento
casuale, per poi tradurla in una variabile casuale.
Alcuni schemi teorici:
Schema teorico di riferimento:
Esperimento tipo:
Modello di v. c.:
• 1 prova con risultato dicotomico
• Lancio moneta (successo-insuccesso) • Bernoulli
• n prove con risultato dicotomico
• lancio della moneta n volte (numero
di successi in n prove)
• Binomiale, Poisson
• Equiprobabilità
• Lancio del dado
• Uniforme
• Simmetria intorno alla media
• Misura (fenomeni continui)
• Normale
Se si riesce a risalire ad una variabile casuale nota, ossia di cui si conosce la
distribuzione di probabilità, il calcolo delle probabilità per i diversi valori della
variabile statistica è immediato.
13
Famiglie di variabili casuali
Normale
Bernoulli
Binomiale
Ipergeometrica
Geometrica
Binomiale Negativa
Poisson
Uniforme
Esponenziale
Gamma
Chi-quadrato
T di Student
F di Fisher
Cauchy
Lognormale
Logistica
Laplace
Beta
Pareto
Weibull
14