Triangolo rettangolo

Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
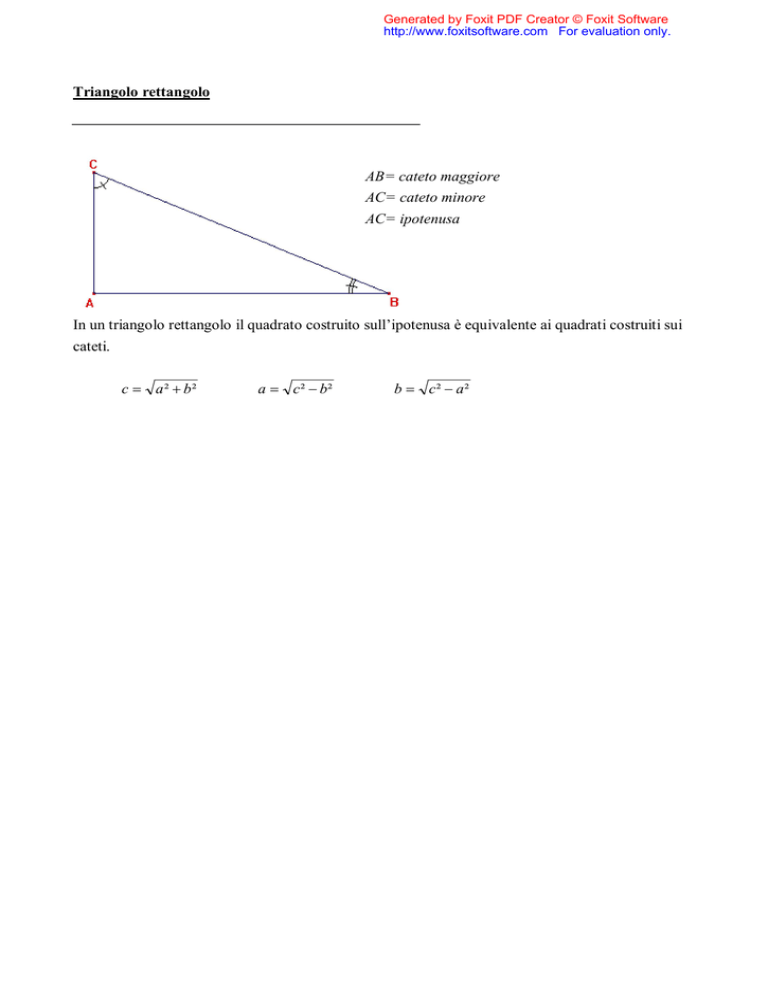
Triangolo rettangolo
AB= cateto maggiore
AC= cateto minore
AC= ipotenusa
In un triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente ai quadrati costruiti sui
cateti.
c  a ²  b²
a  c ²  b²
b  c²  a²
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
Triangolo rettangolo isoscele (triangolo emiquadrato)
Il triangolo rettangolo isoscele è la metà di un quadrato.
AB= a (cateto)
BD= c (ipotenusa)
 i cateti sono congruenti (AB=AD)
 Gli angoli acuti misurano 45° (B=D).
1. Se conosci il cateto:
 L’ipotenusa è uguale al cateto per radice di due
ca 2
2. Se conosci l’ipotenusa:
 Il cateto è uguale all’ipotenusa fratto la radice di due
a
c
2
Problemi
Un quadrato ha il lato 15 cm. Calcola la lunghezza della diagonale.
d  l 2  15 2cm
Un triangolo rettangolo isoscele ha l'ipotenusa lunga 20 cm. Calcola la lunghezza del cateto.
a
c
2

20
2

400
 200  10 2cm
2
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
Triangolo rettangolo con gli angoli di 30° e 60° (triangolo emiquilatero)
Il triangolo rettangolo avente gli angoli acuti di 30° e 60° è la metà di un triangolo equilatero.
In questo triangolo
 il cateto minore è opposto all’angolo di 30°
(AB=a)
 il cateto maggiore è opposto all’angolo di
60° (AC=b)
Come si calcola un lato conoscendo l’altro
1. Se conosci il cateto minore:
 L’ipotenusa è uguale al doppio del cateto
minore
 Il cateto maggiore è uguale al cateto minore
per la radice di tre
ba 3
c  2a
2. Se conosci il cateto maggiore:
 Il cateto minore è uguale al cateto maggiore fratto la radice di tre
 L’ipotenusa è uguale al doppio del cateto maggiore fratto la radice di tre
a
b
3
c2
b
3
Problemi
Un triangolo equilatero ha il lato lungo 24 cm. Calcola l’altezza.
h  l 3  24 3cm
Un triangolo rettangolo ha un angolo acuto di 60° e il cateto maggiore lungo 30 cm. Clacola la
lunghezza dei lati.
a
b
3

30
3

c  2a  20 3cm
900
 300  10 3cm
3