Test chi-quadrato di indipendenza

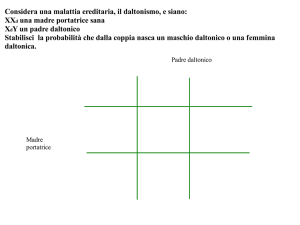
Test chi-quadrato di indipendenza
X e Y sono due variabili QUALITATIVE e si vuole verificare se sono indipendenti.
La definizione di indipendenza nel caso di variabili qualitative e’ la seguente:
P[ X  xi , Y  y j ]  P[ X  xi ]P[Y  y j ] , per ogni valore di i e j
Il modo piu’ intuitivo di scrivere le ipotesi del test di indipendenza e’ il seguente :
 H 0 : P[ X  xi , Y  y j ]  P[ X  xi ]P[Y  y j ]

 H1 : P[ X  xi , Y  y j ]  P[ X  xi ]P[Y  y j ]
ESEMPIO
Le variabili X e Y sono :


X : colore degli occhi (modalita’ CHIARI e SCURI)
Y : colore dei capelli (modalita’ BIONDI, CASTANI e NERI)
I dati relativi ad un campione di dimensione n=50 sono rappresentati nella
seguente tabella dei conteggi:
CAPELLI
O
BIONDI
CASTANI
NERI
TOTALE
C
CHIARI
10
10
2
22
C
SCURI
10
12
6
28
H
TOTALE
20
22
8
50
I
La tabella seguente rappresenta le frequenze :
O
C
C
H
I
CHIARI
SCURI
TOTALE
BIONDI
0.2
0.2
0.4
CAPELLI
CASTANI
0.2
0.24
0.44
NERI
0.04
0.12
0.16
TOTALE
0.44
0.56
1
Per poter effettuare un test e’ necessario costruire una statistica test T .
In generale si ha che :
T  n
i, j
f
ij  f i f
fi f
j

2
 2  ( I  1)( J  1)   2  2
j
In questo caso :
 n rappresenta il numero di elementi del campione
 I rappresenta il numero di livelli della variabile X (I=2)
 J rappresenta il numero di livelli della variabile Y (J=3)
Utilizzando la precedente tabella si possono ricavare i valori :
CAPELLI
BIONDI
CASTANI
0.176
0.1936
O
C
CHIARI
C
SCURI
0.224
H
TOTALE
0.4=fBiondi.
NERI
0.0704
TOTALE
0.44=f.Chiari
0.2464
0.0896
0.56=f.Scuri
0.44= fCastani.
0.16= fNeri.
f..
I
Il livello a cui si vuole effettuare il test e’ 5%.
La statistica test T e’ la seguente :
T   2 ( I 1)( J 1)   2  2
Dalle tavole si ottiene :
P   2  2  5.99   0.05 e quindi la regione di rifiuto vale R= (5.99,+)
Il valore della statistica T relativa ai dati del campione e’
  0.2  0.176 2  0.2  0.1936 2  0.04  0.0704 2  0.2  0.224 2  0.24  0.2464 2  0.12  0.0896 2 
t





  50
0.176
0.1936
0.0704
0.224
0.2464
0.0896


= 1.49 .
Poiche’ il valore di t non appartiene a R (tR) si accetta l’ipotesi H0, cioe’
che X e Y sono indipendenti.