Similitudine
Sul triangolo isoscele inscritto in una circonferenza ed una corda
Problema
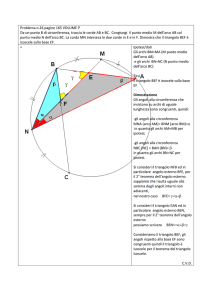
Il triangolo isoscele ABC è inscritto nella circonferenza di centro O. Detta CE una corda della
circonferenza che interseca la base AB in D, dimostrare che il lato AC è medio proporzionale tra
CD e CE.
(Suggerimento: Unire E con A e B)
Dimostrazione
In riferimento alla figura riportata a lato occorre dimostrare che sussiste la seguente proporzione:
CD : AC = AC : CE
Per la dimostrazione della tesi proveremo che sono simili i
triangoli BCD e BCE.
Cominciamo con l’osservare che i suddetti triangoli hanno
l’angolo nel vertice C in comune. Inoltre, notiamo che l’angolo
del triangolo BCD è angolo alla circonferenza che
C BD
del triangolo BCE è
insiste sull’arco AC e che l’angolo BEC
. Poiché i
angolo alla circonferenza che insiste sull’arco BC
sono sottesi rispettivamente dalle corde
due archi AC , BC
AC, BC, che sono congruenti in quanto lati del triangolo
isoscele ABC sulla base AB, si deduce che sono congruenti i
suddetti archi e quindi che sono congruenti anche gli angoli
, BEC
che su tali archi insistono.
C BD
A questo punto possiamo concludere che i due triangoli sono congruenti per il primo criterio di
similitudine avendo due angoli ordinatamente congruenti. Ne segue che risultano congruenti anche i
≅ C BE
.
terzi angoli: BDC
Dalla similitudine dimostrata deduciamo le seguenti coppie di lati omologhi (BC; CE), (CD; BC),
(BD; BE) e dunque che sussiste la proporzione
CD : BC = BC : CE
Poiché BC≅AC, sostituendo nella precedente proporzione BC con AC si ottiene la tesi.
Luigi Lecci: www.matematicaescuola.it