CORSO DI LAUREA IN SCIENZE BIOLOGICHE
Prova scritta di FISICA – 13 gennaio 2009
1) Meccanica:
Una slitta di massa m=12 Kg si muove lungo un piano inclinato di 30°, lungo s =10 metri. Sapendo
che il coefficiente di attrito dinamico slitta-piano è = 0.15, si calcoli:
a) la forza , parallela al piano inclinato, con cui la slitta deve essere tirata per farla salire con velocità
costante.
b) la velocità con cui raggiunge la base del piano inclinato, partendo dalla sommità con velocità
nulla e con a bordo un bimbo di massa M=15 kg .
2) Elettrostatica:
Nel punto P (0, d) di un sistema di assi (x,y) di origine O è fissata una carica q positiva. Nel punto R
(0, - 2d) è fissata un’ altra carica qx, positiva. Sapendo che q = 2 nC e d = 10 cm , calcolare :
a) il valore di qx in modo tale che il campo elettrico in O sia nullo
b) il potenziale nel punto O nel caso in cui qx sia pari a q e nel caso in cui qx abbia il valore
trovato al punto a).
(0 = 8.85 10-12 C2/Nm2 ).
3) Fluidi:
In un liquido ideale di densità l= 0.7 g/ cm3 è totalmente immerso , appeso ad una fune, un cubetto
di alluminio ( densità Al = 2.7 g/ cm3 ) di lato L= 10 cm.
a) Si calcoli la tensione della fune.
b) Si ripeta il calcolo supponendo che il cubetto, totalmente immerso , abbia al suo interno una
cavità sferica, in cui c’è il vuoto, di raggio r=3 cm.
4) Termodinamica:
Due moli di un gas perfetto monoatomico compie un ciclo reversibile a partire dallo stato iniziale A, in
cui la pressione pA = 6 105 Pa e il volume VA = 2 10–3 m3 , costituito dalle seguenti trasformazioni
AB: la pressione aumenta linearmente con il volume ed inoltre pB = 2 pA e VB = 3 VA ;
BC: isovolumica con pC = pA;
CA: isobara.
a) si disegni il ciclo in un diagramma p, V e si calcoli il lavoro compiuto dal gas nelle trasformazioni
AB e CA.
b) si calcoli la quantità di calore scambiata dal gas nell’intero ciclo.
(Nota: R= 8.31 J/Kmole =0.082 l atmo /Kmole)
SCRIVERE IN MODO CHIARO. GIUSTIFICARE BREVEMENTE I PROCEDIMENTI.
SOSTITUIRE I VALORI NUMERICI SOLO ALLA FINE. NON SCORDARE LE UNITA`
DI MISURA. Testi, soluzioni ed esiti alle pagine: www2.fisica.unimi.it/bettega/ (AD),
fisbio.webhop.net (EN), www.mi.infn.it/~sleoni (OZ)
Soluzione Esercizio 1
a. La forza risultante agente sulla slitta è nulla quando la slitta si muove con velocità costante .
Scelto il semiasse positivo x, parallelo al piano e con verso concorde a quello del moto ( verso
l’alto), deve pertanto essere:
F – mg sen 30° - mg cos 30° = 0
dove F, -mgsen30° e - mg cos 30° sono le componenti lungo l’asse x rispettivamente della forza
con cui tirare la slitta, della forza peso e della forza di attrito.
Sostituendo i valori numerici si trova F 74.1 N
b. Durante la discesa lungo il piano inclinato agisce la forza peso, la cui componente lungo l’asse x
è concorde con il verso del moto, e la forza di attrito , con verso opposto a quello del moto. Il lavoro
compiuto dalla risultante della forza peso e della forza di attrito uguaglia la variazione dell’energia
cinetica della slitta con il bimbo nel tratto percorso lungo il piano inclinato ( teorema lavoro energia cinetica ) , pertanto:
(( m +M)g sen 30° - (m+ M) g cos 30°) s = ⅟₂ (m+ M) v2fin - ⅟₂ (m+ M) v2iniz
L’energia cinetica iniziale ⅟₂ (m+ M) v2iniz è nulla , sostituendo i valori numerici si ottiene pertanto:
vfin = 8.5 m/s
Soluzione Esercizio 2
a. Il campo elettrostatico creato in O dalla carica q fissata in P vale :
Eq = (q / 40 d2 ) (- j )
Il campo elettrostatico creato in O dalla carica qx fissata in R vale :
Eqx = (qx / 160 d2 ) ( j ).
I due campi hanno verso opposto, pertanto affinchè il campo totale in O sia nullo i due campi
devono avere lo stesso modulo:
( q / 40 d2 ) = (qx / 160 d2 )
da cui, sostituendo i valori numerici , si ottiene
qx = 4 q = 8 nC.
b. Il potenziale in O dovuto alle due cariche è
V(O) = ( q /40 d) + ( qx /80 d)
Se qx = q , V = 270 Volt
Se qx = 4q , V = 540 Volt
Soluzione Esercizio 3
a. Agiscono sul cubetto immerso nel fluido la forza peso, P= mg, la spinta di Archimede S =
mliq g , peso del fluido spostato , opposta alla forza peso , la tensione della fune T, opposta alla
forza peso .
All’equilibrio, il modulo della tensione T vale :
T= mg – mliq g = Al V g - l V g dove V è il volume del cubetto.
Sostituendo i valori numerici si ottiene T= 19.6 N
b. Nel caso in cui nel cubetto ci sia una cavità di volume Vcavità, il peso del cubetto sarà
Al ( V - Vcavità ) g, mentre la spinta Archimedea non varia ed è l V g .
La tensione della fune è pertanto:
T= Al ( V - Vcavità ) g - l V g
Vcavità = ( 4/3) π r 3
Sostituendo i valori numerici si ha .
T = 16.7 N
Soluzione Esercizio 4
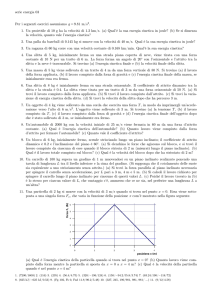
a. La figura mostra il ciclo in un diagramma pV :
In un diagramma di questo tipo il Lavoro compiuto dal gas nelle trasformazioni AB e CA è pari
all’area delimitata dalle trasformazioni stesse e dall’asse V, tra lo stato iniziale e quello finale.
Pertanto:
LAB = (pB + pA ) (VB-VA) /2 = (2pA+pA)(3VA-VA) /2= 3pAVA = 3600 J
LCA = (VA- VC ) pA= (VA-3VA)pA=-2pAVA = -2400 J
b. La variazione di energia interna relativa all’intero ciclo è nulla e pertanto la quantità di calore
scambiata nell’intero ciclo è uguale al lavoro compiuto dal gas nell’intero ciclo.
Il lavoro totale è la somma di quello compiuto nella trasformazione AB e nella trasformazione CA
(quello relativo alla trasformazione BC è nullo) .
La quantità di calore scambiata nell’intero ciclo è pertanto
Qtot= 3600 J- 2400 J = 1200 J.