TEOREMA DI TALETE
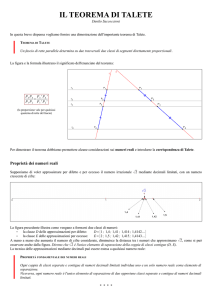
Questo teorema sostiene che: “un fascio di rette parallele tagliato da due trasversali forma due
famiglie di segmenti direttamente proporzionali”
Andiamo ad analizzarlo
Una retta trasversale che interseca una retta di un fascio interseca anche tutte le altre.
Sono corrispondenti: i punti (A,A’,B,B’,C,C’, etc..)e i segmenti(AB,A’B’,etc..).
In sostanza AB/BC=AB’/BC’
Ipotesi
Tesi
Dimostrazione
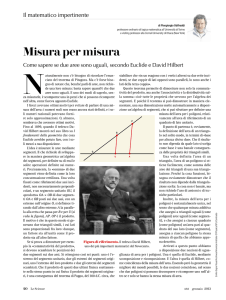
Dato un triangolo ABC, tagliato da un segmento DE parallelo a BC.
Si congiungano D con C ed E con B, ottenendo due triangoli BDE e CDE.
Tali triangoli sono equivalenti, in quanto hanno la stessa base e stessa altezza (tale altezza sarebbe la distanza tra DE e
BC).
Quindi possiamo tranquillamente scrivere:
Ma, avendo CDE e ADE la stessa altezza (col piede sul lato AC), si può dedurre che il rapporto tra le aree è uguale al
rapporto delle basi:
Per la stessa ragione:
Unendo le ultime due proporzioni possiamo così ottenere che:
Conseguenze del teorema di Talete
-se per il punto medio di un lato di un triangolo si traccia la parallela ad un altro lato, questa taglia il terzo
lato nel suo punto medio
-viceversa, se si congiungono i punti medi di due lati di un triangolo, il segmento ottenuto è parallelo al terzo
lato ed è inoltre congruente alla sua metà.
ESERCIZI PER LA CLASSE:
1) Nel triangolo ABC si ha AC=18 cm e BC=15 cm. Se D è un punto di AC tale che CD=12
cm, a che distanza da B si deve prendere un punto E, appartenente a CB, in modo che risulti DE
// AB?
2) Tre rette parallele determinano su una trasversale due segmenti consecutivi che misurano 7a
e 8a. Al segmento somma di questi due, corrisponde su un’ altra trasversale, un segmento che
misura 105a. Determinare le misure corrispondenti dei segmenti dati sopra la seconda
trasversale.
3) Quattro rette parallele staccano su una trasversale tre segmenti consecutivi le cui misure
sono: a, 4a, 2a. La somma di questi tre segmenti ha per corrispondente, sopra una seconda
trasversale, un segmento di misura 8a. Quanto misurano, sulla seconda trasversale, i
corrispondenti dei tre segmenti inizialmente considerati?
Soluzione esercizio n. 1:
Svolgimento
Dati: AC=18cm; BC=15; CD=12cm
Ipotizzando che DE//AB, abbiamo per costruzione che i triangoli BAC ed EDC sono simili, avendo
un angolo in comune e 2 angoli corrispondenti rispetto alla rispettiva trasversale.
Essendo i triangoli simili, allora i lati omologhi sono in proporzione tra loro: DC/AC = EC/BC,
12/18=EC/15
quindi avremo: (12x15):18= 10cm
Di conseguenza calcoleremo BE:
BC-EC= (15-10)= 5cm
SOLUZIONE ESERCIZIIO N°2
Dati: AB=7°;BC=8°;DF=105°
Le nostre incognite sono: DE=x; EF=y
Quindi: x+y 105a
Per il teorema di Talete sappiamo inoltre che i lati sono in proporzione tra loro, ovvero:
x/7a=y/8a
x=7/8y
Sostituendo nella precedente otteniamo:
7/8y+y=105a 15/8y=105a
Y=56a
x=49a
SOLUZIONE ESERCIZIO N°3
Dai dati avremo: AB=a
BC=4a
CD=2a
EH=8a
Di conseguenza avremo anche che: AD=7a
Sfruttiamo questa condizione, applicando il teorema di Talete, per risolvere il problema:
EF:AB=EH:AD
EF=ABxEH/AD=ax8a/7a
FG:BC=EH:AD
FG=BCxEH/AD=4ax8a/7a=32/7a
GH;CD=EH:AD
GH=CDxEH/AD=2ax8a/7a=16/7a