Il teorema di Talete in breve
Attribuito a Talete di Mileto che ne era sicuramente a conoscenza ma
tale relazione era già nota agli antichi babilonesi. La prima
dimostrazione di cui si abbia documentazione è di Euclide (III sec
a.C. Elementi VI 2).
TEOREMA
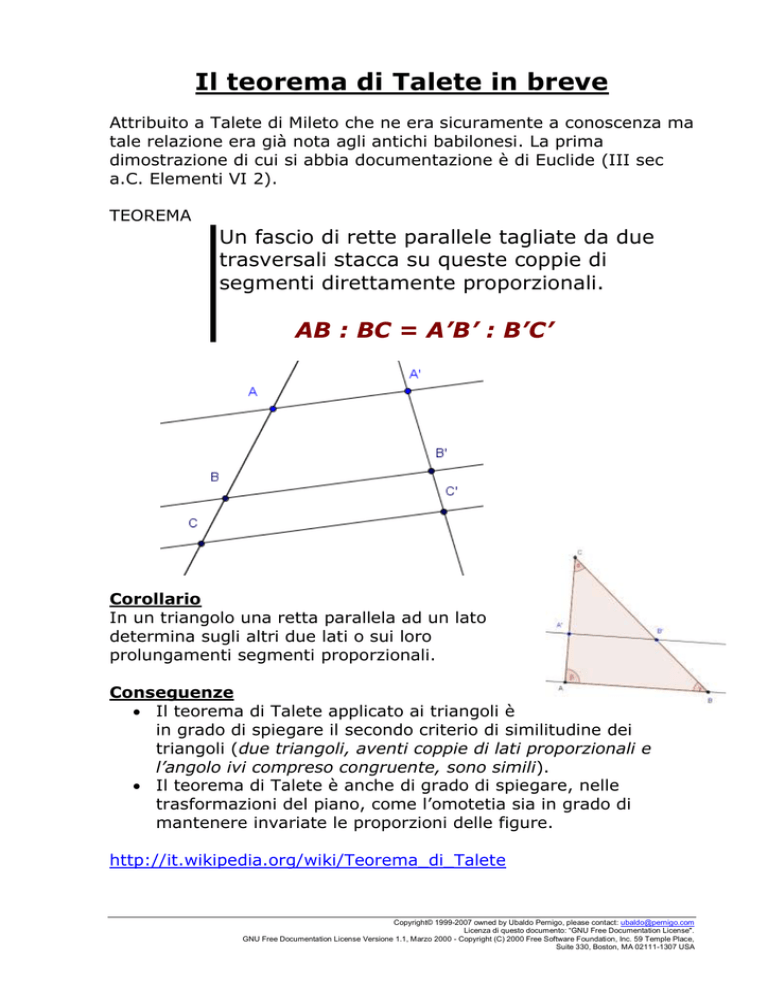
Un fascio di rette parallele tagliate da due
trasversali stacca su queste coppie di
segmenti direttamente proporzionali.
AB : BC = A’B’ : B’C’
Corollario
In un triangolo una retta parallela ad un lato
determina sugli altri due lati o sui loro
prolungamenti segmenti proporzionali.
Conseguenze
Il teorema di Talete applicato ai triangoli è
in grado di spiegare il secondo criterio di similitudine dei
triangoli (due triangoli, aventi coppie di lati proporzionali e
l’angolo ivi compreso congruente, sono simili).
Il teorema di Talete è anche di grado di spiegare, nelle
trasformazioni del piano, come l’omotetia sia in grado di
mantenere invariate le proporzioni delle figure.
http://it.wikipedia.org/wiki/Teorema_di_Talete
Copyright© 1999-2007 owned by Ubaldo Pernigo, please contact: [email protected]
Licenza di questo documento: “GNU Free Documentation License".
GNU Free Documentation License Versione 1.1, Marzo 2000 - Copyright (C) 2000 Free Software Foundation, Inc. 59 Temple Place,
Suite 330, Boston, MA 02111-1307 USA












