Principi di Economia – Microeconomia
Esercitazione 2 – Elasticità
Soluzioni
Novembre 2016
1. Considerate il mercato della carne di maiale negli Stati Uniti. La tabella
seguente mostra le quantità di carne di maiale acquistate ogni anno in
corrispondenza dei diversi prezzi.
Prezzo
Quantità
(€ al kg) (milioni di kg)
14,3
0
10,3
80
4,3
200
3,3
220
2,3
240
0
286
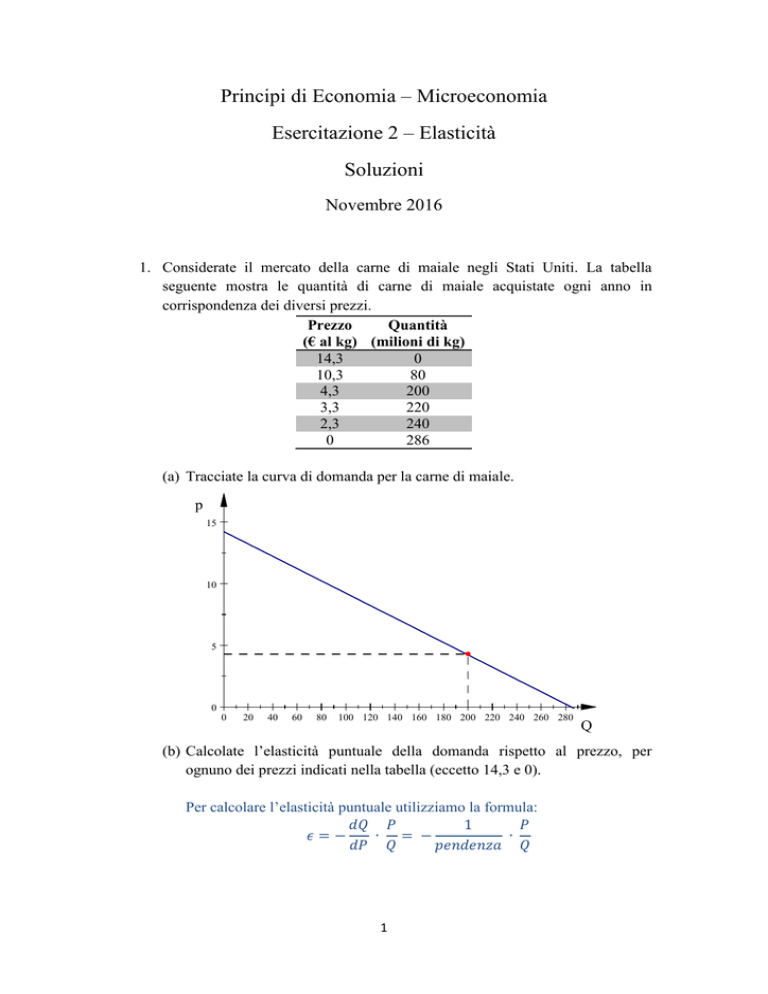
(a) Tracciate la curva di domanda per la carne di maiale.
p
15
10
5
0
0
20
40
60
80
100 120 140 160 180 200 220 240 260 280
Q
(b) Calcolate l’elasticità puntuale della domanda rispetto al prezzo, per
ognuno dei prezzi indicati nella tabella (eccetto 14,3 e 0).
Per calcolare l’elasticità puntuale utilizziamo la formula:
1
∙ ∙
1
Se la funzione di domanda fosse esplicitata, nel nostro caso sarebbe Q(p) =
286 – 20p. In tal caso utilizzeremmo la formula canonica per il calcolo
dell’elasticità, ovvero ∙ .
Innanzitutto calcoliamo la pendenza della curva di domanda, pari al
rapporto fra l’intercetta verticale e l’intercetta orizzontale cambiato di
segno: ,
0,05 . Questa misura ci dice che, per vendere
un milione di kg di carne in più all’anno, il prezzo al kg dovrà diminuire di
5 centesimi di euro. Possiamo quindi calcolare l’elasticità per ogni valore
del prezzo, utilizzando la formula di cui sopra:
-
Per p = 10,3:
-
Per p = 4,3:
-
Per p = 3,3:
-
Per p = 2,3:
∙
,
,
2,575
∙ 0,43
,
∙ 0,3
∙
,
≃ 0,2
(c) Supponete che il prezzo passi da 10,3 € a 11,3 €. Siete in grado di dire,
senza fare ulteriori calcoli, come varieranno i ricavi per i produttori di
carne?
Poiché l’elasticità della domanda in corrispondenza del prezzo p=10,3 è
maggiore dell’unità (domanda elastica), un aumento del prezzo farà
diminuire i ricavi.
Richiamando la formula che lega la derivata della funzione dei ricavi
all’elasticità:
#
# #
"
# $ # ∙
# %1 $
∙ & '1 (#
#
# #
#
Possiamo notare che in corrispondenza di p=10,3, la derivata della
funzione dei ricavi è negativa:
"
"
'1 2,575( ∙ 80 80 206 126 ⇒
,0
,
,
(d) Calcolate la variazione dei ricavi dei produttori di carne se il prezzo passa
da 3,3 € a 4,3 €.
A 3,3€ al kg vengono venduti 220 milioni di kg di carne, realizzando un
ricavo pari a: " # ∙ # 3,3 ∙ 220 726 (milioni di euro).
Se il prezzo sale a 4,3€, la quantità venduta scende a 200 milioni di kg e i
ricavi saranno 4,3 ∙ 200 = 860 milioni di euro.
I ricavi sonno aumentati; in corrispondenza del tratto inelastico della curva
di domanda, un aumento del prezzo si traduce in un aumento dei ricavi (la
riduzione della quantità venduta è più che compensata dall’aumento dei
prezzi).
2
2. Considerate due mercati: il mercato dei farmaci e quello dei computer. Il
primo mercato presenta una curva di domanda rigida (il consumo di farmaci
reagisce poco alle variazioni di prezzo), mentre la domanda di computer è
elastica. Supponete che un’innovazione tecnologica faccia raddoppiare
l’offerta di entrambi.
(a) Cosa accade al prezzo di equilibrio e alla quantità scambiata in ciascun
mercato?
In entrambi i mercati l’aumento dell’offerta fa diminuire i prezzi ed
aumentare le quantità scambiate.
(b) Quale dei due beni subisce la variazione più rilevante di prezzo? E di
quantità?
Il prezzo diminuisce maggiormente nel mercato dei farmaci dove, essendo
la domanda inelastica, si assiste ad un modesto incremento della quantità.
Nel mercato dei computer, l’elevata elasticità comporta un sensibile
aumento della quantità scambiata ed una più contenuta variazione dei
prezzi.
(c) Cosa accade alla spesa totale dei consumatori in ciascun mercato?
La spesa totale dei consumatori coincide con il ricavo totale dell’industria
in ciascun mercato.
Nel mercato dei farmaci il ricavo totale diminuisce: in un mercato
caratterizzato da domanda rigida, una diminuzione del prezzo produce un
aumento meno che proporzionale della quantità domandata.
Nel mercato dei computer, invece, il ricavo totale aumenta: in un mercato
caratterizzato da domanda elastica, una diminuzione del prezzo produce un
aumento più che proporzionale della quantità domandata.
3. Considerate un consumatore con la seguente funzione di domanda per il bene
x:
- = 80 – 1,2px + 2py + 0,03Y
dove px e il prezzo del bene in questione, py e il prezzo di un altro bene e Y il
suo reddito.
(a) Assumendo che px = 20, py = 2 e Y = 90000, calcolate la quantità di bene x
domandata dal consumatore, - .
- 80 1,2 ∙ 20 $ 2 ∙ 2 $ 0,03 ∙ 90000 2760
3
(b) Qual è l’elasticità della domanda di x rispetto al suo prezzo?
L’elasticità è data da:
1 20
∙ 1,2 ∙
≃ 0,008
1
- 2760
Nota bene: Nel mercato la maggior parte dei beni scambiati sono beni
ordinari (i.e. all’aumentare del loro prezzo la domanda di tali beni si
riduce), per questo la formula per calcolare l’elasticità di domanda viene
scritta con un meno davanti.
/-0 (c) E l’elasticità della domanda di x rispetto al reddito?
L’elasticità di domanda rispetto al reddito e data da:
1 3
90000
2- ∙ 0,03 ∙
≃ 0,978
13 2760
(d) Qual è l’elasticità incrociata, ovvero l’elasticità della domanda del bene x
rispetto al prezzo del bene y?
L’elasticità incrociata è pari a:
1 5
2
/-4 ∙
2∙
6 0,001
1
5 2760
(e) Sulla base dei risultati del punto precedente, argomentando le vostre
conclusioni, dite se:
• i beni x e y sono, per questo consumatore, complementi o sostituti;
Sono beni sostituiti: /-4 7 0, ovvero al crescere del prezzo di y la
quantità domandata di x aumenta.
Soluzione alternativa:
80
8/4
7 0. Ovvero, al crescere del prezzo di y
aumenta la quantità acquistata di x. Un esempio di beni sostituiti: il
bene x è il caffe e il bene y è il te.
•
se il bene x è inferiore o normale (ed eventualmente se è necessario o
di lusso).
Il bene x è normale, dato che l’elasticità della sua domanda rispetto al
reddito è positiva: 2- 7 0.
In particolare, il bene x è un bene necessario, poiché l’elasticità al
reddito e inferiore all’unita: 2- ∈ '0, 1(.
4












