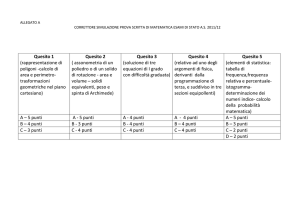
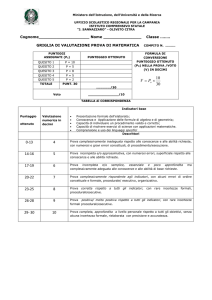
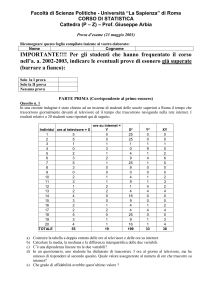
Proposta di soluzione della prova di matematica
Liceo scientifico di Ordinamento - 2014
Problema 1
Punto a) Osserviamo che g ′ (x) = f (x) e pertanto g ′ (0) = f (0) = 0
in quanto Γ è tangente all’asse delle ascisse, mentre g ′ (k) = f (k) = 0
in quanto x = k è punto di massimo.
Inoltre f passa per i punti (0, 0), (k, 0) ed avendosi f ′ (x) = g ′′ (x) e
g ′′ (h) = 0 a causa della presenza del flesso e che
g ′′ (x) < 0 x ∈ (h, w),
g ′′ (x) > 0, x ∈ (0, h)
segue che
f cresce su (0, h)
f decresce su (h, w)
f ha un massimo in x = h
Avendosi pure
f (x) > 0 ⇔ x ∈ (0, k)
f (x) < 0 ⇔ x ∈ (k, w)
il grafico della funzione f è il seguente:
Punto b) Poniamo g(x) = ax3 + bx2 + cx + d da cui
g ′ (x) = 3ax2 + 2bx + c, g ′′ (x) = 6ax + 2b
1
2
Abbiamo
g(0) = 0 ⇒ d = 0
g(w) = 0 ⇒ aw2 + bw + c = 0
g ′ (0) = 0 ⇒ c = 0
g ′ (k) = 0 ⇒ 3ak + 2b = 0
g ′′ (h) = 0 ⇒ 6ah + 2b = 0
e quindi
aw + b = 0
3ak + 2b = 0
6ah + 2b = 0
Sottraendo la terza dalla seconda si ha 3ak − 6ah = 0 ⇒ k = 2h,
mentre, poiché dalla prima si ha b = −aw, sostituendo nella terza
6ah − 2aw = 0 ⇒ w = 3h. Ciò mostra che l’intervallo [0, w] è
suddiviso nei tre intervalli di uguale ampiezza [0, h], [h, 2h], [2h, 3h].
Punto c) Se w = 3 allora h = 1. Inoltre abbiamo, da quanto visto
in precedenza, g(x) = ax3 + bx2 . Ne segue che
2
g(3) = 0 = 27a + 9b
=a+b
3
e quindi dalla seconda b = −3a che sostituito nella prima porta
a = − 31 . In definitiva
g(1) =
1
g(x) = − x3 + x2
3
Poiché la funzione assume il valore cercato in x = 1 abbiamo
−x3 + 3x2 = 2 ⇒ x3 − 3x2 + 2 = 0
e potendo scomporre
x3 − 3x2 + 2 = (x − 1)(x2 − 2x − 2)
√
si ricavano le ulteriori soluzioni x = 1 ± 3, delle quali risulta accettabile solo quella col segno positivo. I due punti sono allora
√
H(1, 2/3), P (1 + 3, 2/3)
Poiché g ′ (x) = −x2 +2x segue che i coefficienti angolari delle tangenti
nei due punti sono rispettivamente
√
√
g ′ (1) = 1,
g ′ (1 + 3) = 6 + 4 3
da cui le equazioni delle normali
3
y−
√
2
2
1
√ (x − 1 − 3)
= −(x − 1)y − = −
3
3
6+4 3
Punto d) Il volume del solido di rotazione intorno all’asse y può
essere visto come la somma infinita delle superfici laterali dei cilindri
di raggio x e altezza g(x) al variare di x tra a e b, per cui si può
esprimere il volume come
∫
b
(2π)x g(x) dx
a
Abbiamo allora
(
)
)
∫ 3
∫ 3( 4
1 3
x
2
3
(2πx) − x + x
− +x
dx = 2π
dx =
3
3
0
0
]3
[ 5
81π
x4
81π
x
dm3 =
dm3 =
litri
2π − +
15
4 0
10
10
Problema 2
Punto a) Abbiamo
√
−2x
4 − x2 − x2
4 − 2x2
2
√
√
√
f (x) = 4 − x + x ·
=
=
=0
2 4 − x2
4 − x2
4 − x2
√
√
da cui i √
punti stazionari x = ± 2 e quindi il massimo ( 2, 4) e il
minimo (− 2, 4)
′
Punto b) Poiché
√
f (−x) = −x 4 − x2 = −f (x)
la funzione risulta simmetrica rispetto all’origine. Inoltre f ′ (0) = 2
e quindi l’angolo che la retta tangente forma con l’asse delle ascisse
risulta pari a
α = arctan(2) ≈ 63, 43◦ ≈ 63◦ 26′
4
Punto c) La curva in questione è composta dai due rami della curva
y = ±f (x) i quali coincidono con il grafico dato e con il suo simmetrico
rispetto all’asse delle ascisse. L’area racchiusa da tale curva vale, pertanto, 4 volte l’area compresa sotto il grafico dato sull’intervallo [0, 2]
e quindi
∫
∫
2
A=4
f (x) dx = 4
0
∫
−2
0
2
∫
√
2
x 4 − x dx = 4
0
2
0
2
√
1
− ·(−2x) 4 − x2 dx =
2
√
]2 32
2[
4 − x2 d(4 − x2 ) = −2 · (4 − x2 )3/2 0 =
3
3
Punto d) Osserviamo che la funzione assume il valore 1 solo quando
f (x) = π/2 + kπ, k ∈ Z. Tuttavia, poiché f ([0, 2]) = [0, 4], l’unico
valore accettabile si ha per f (x) = π/2 che ricade nell’immagine della
funzione. Ne segue che
√
π
x 4 − x2 =
2
2
2
4x (4 − x ) = π 2
4x4 − 16x2 + π 2 = 0
Risolvendo si trovano le soluzioni
√
16 − π 2
=
2
entrambe positive e quindi le soluzioni accettabli
√
√
4 ± 16 − π 2
x=
2
I punti in cui h = 1 sono massimi assoluti, mentre è facile vedere che
non vi sono punti per cui h = −1 in quanto dovrebbe aversi f (x) =
3π/2 che non appartiene all’immagine di cui√sopra. Tuttavia h′ (x) =
cos(f (x)) · f ′ (x) e si annulla o quando x = 2 o quando f (x) = π/2.
Questi ultimi due punti sono quelli appena
calcolati in cui si ha massimo
√
assoluto,
√ mentre per
√ il punto x = 2 abiamo un minimo relativo pari
a h( 2) = sin(f ( 2)) = sin(2) > 0. Inoltre nei punti x0, x = 2 si
hanno i minimi assoluti pari a zero.
Osservando il grafico della funzione h, si osserva che i valori di k per
i quali si hanno 4 intersezioni sono quelli nell’intervallo (sin(2), 1)
x21,2
4±
5
Quesito 1
Sappiamo che in un triangolo qualunque vale la seguente relazione
tra lati e angoli:
a
b
c
=
=
sin α
sin β
sin γ
Nel nostro caso abbiamo:
4
3
=
sin α
sin 30◦
⇒ sin α =
4
2
2
sin 30◦ =
⇒ α = arcsin ≈ 41◦ 48′
3
3
3
Quesito 2
6
Esiste un teorema che assicura che la somma degli angoli che formano
le facce di un angolo solido è minore di un angolo giro.
• Notiamo che ad ogni vertice concorrono almeno 3 facce, e che la
somma delle ampiezze degli angoli che concorrono in quel vertice deve
essere minore di 360◦
Esistono quindi solo 5 poliedri regolari:
A) Tre hanno come facce triangoli rettangoli.
• 3 · 60◦ = 180◦ TETRAEDRO REGOLARE
• 4 · 60◦ = 240◦ OTTAEDRO REGOLARE
• 5 · 60 = 300◦ ICOSAEDRO REGOLARE
B) Uno ha come facce quadrati:
• 3 · 90 = 180◦ CUBO
C) Uno ha come facce pentagoni regolari:
• 3 · 108◦ = 270◦ DODECAEDRO REGOLARE
D) Non esistono poliedri regolari che hanno come facce esagoni regolari: infatti si avrebbe
3 · 120◦ = 360◦ [IMPOSSIBILE]
Quesito 3
(2a2 − 3b3 )n
Sviluppando compare il termine −1080a4 b9
Vogliamo determinare il valore di n
Lo sviluppo della(potenza
) di un binomio qualsiasi è dato da:
∑
n
n
(a + b)n = k=0
an−k bk
k
Quindi otteniamo −1080a4 b9 quando dovremo moltiplicare il quadrato
di 2a2 col cubo di −3b3 . Ciò implica che la somma degli esponenti dei
termini (che è pari al valore cercato) risulta n = 2 + 3 = 5
Quesito 4
Osserviamo che possiamo calcolare il volume attraverso la formula
∫
−1
V =
A(x) dx
−2
dove A(x) è l’area delle sezioni verticali del solido per ogni x fissato.
Per calcolare tale area, è sufficiente notare che le sezioni risultano dei
rettangoli di altezza h(x) e base f (x) e pertanto
7
∫
∫
−1
V =
−2
−2
posto t = 1/x dt = −1/x dx,
−1/2
2
∫
V =
−1
A(x) dx =
1 1/x
e dx =
x2
x = −1 → t = −1, x = −2 → t =
[
]−1
1
1
−et dt = −et −1/2 = −e−1 + e−1/2 = √ −
e e
−1/2
−1
Quesito 5
Vogliamo calcolare quanti sono i numeri tra 1 e 6000 non divisibili
né per 2, né per 3, né per 5. Tra 1 e 6000 ci sono 3000 numeri divisibili
per 2. A questi ne dobbiamo aggiungere 1000 divisibili per 3 (ma non
anche per 2). Poi dobbiamo considerare quelli divisibili per 5 (ma non
anche per 2 o per 3), che risultano essere 400. Quindi i numeri tra 1 e
6000 non divisibili né per 2, né per 3, né per 5 sono
6000 − (3000 + 1000 + 400) = 6000 − 4400 = 1600
Quesito 6
Abbiamo un parallelepipedo a base quadrata di volume pari a 5 litri.
Vogliamo minimizzare la superficie totale del solido sapendo che l2 h = 5
litri = 5dm3 , dove l è il lato del quadrato di base e h l’altezza del solido.
Da: l2 h = 5 ricaviamo h = l52
La funzione da minimizzare è f (l) = 2l2 + 4(l · h) = 2l2 + 20l
4l3 −20
f ′ (l) = 4l − 20
=0
2 =
l
l3
√
3
da cui l = 5 che rappresenta il valore per cui si ha il minimo.
Quesito 7
Il valore medio di f (x) = x nell’intervallo chiuso [0, k] è 9. Cerco k:
Per definizione di valor
abbiamo:
[ medio
]k
√
∫
3
1 k 3
1 x4
3
x
dx
=
=
36 = 3, 3019
9
⇒
9
⇒
k
=
36
⇒
k
=
k 0
k
4
3
0
Quesito 8
8
Sappiamo che un polinomio generico di quarto grado è della forma:
P (x) = a4 x4 + a3 x3 + a2 x2 + a1 x + a0
Per ipotesi sappiamo che
P (1) = 0 ⇔ a4 + a3 + a2 + a1 + a0 = 0
P (2) = 3 ⇔ 16a4 + 8a3 + 4a2 + 2a1 + a0 = 3
P (3) = 3 ⇔ 81a4 + 27a3 + 9a2 + 3a1 + a0 = 3
P ′ (2) = 0 ⇔ 32a4 + 12a3 + 4a2 + a1 = 0
P ′ (3) = 0 ⇔ 108a4 + 27a3 + 6a2 + a1 = 0
Le ultime due le abbiamo perché per x=2 e x=3 P(x) ha il suo valore
massimo. Ora risolvendo il sistema nelle sue 5 inncognite otteniamo i
coefficienti:
a4 = − 34 ; a3 = 15
; a2 = − 111
; a1 = 45; a0 = −24
2
4
Dunque possiamo calcolare: P (4) = −192 + 480 − 444 + 180 − 24 = 0
Quesito 9
√
f (x) = 3 − log2 (x + 5)
Cerco
il dominio di f (x), cioè risolvo il seguente sistema:
{
3 − log2 (x + 5) ≥ 0
x+5>0
Dalla prima otteniamo che 8 ≥ x + 5 ⇒ x ≤ 3.
Dalla seconda otteniamo che x > −5.
La soluzione è pertanto −5 < x ≤ 3 ⇒ x ∈ (−5, 3].
Quesito 10
Cerco: valori reali di x tali che
2
( 51 (x2 − 10x + 26))x −6x+1 = 1
Affinché quest’espressione sia 1 deve accadere, o che la base sia 1 o
che l’esponente sia zero, e cioè che:
A : x2 − 10x + 26 = 5
B : x2 − 6x + 1 = 0
Risolvo dunque queste due equazioni:
A : √ x2 − 10x + 26 = 5 ⇒ x2 − 10x + 21 = 0
x = 5± 25−21
= 5 ± 2 ⇒ x = 3, x =
7
1
√
√
6±
36−4
B : x2 − 6x + 1 = 0 ⇒ x =
3
±
2
=
2
2