TERMODINAMICA DI UNA REAZIONE DI CELLA
INTRODUZIONE
Lo scopo dell’esperienza è ricavare le grandezze termodinamiche per la reazione che avviene in una
cella galvanica, attraverso misure di f.e.m. effettuate a diverse T. La pila in esame è la pila a secco
Ag2O – Zn , utilizzata per alimentare moltissime apparecchiature elettroniche miniaturizzate.
TEORIA
Quando una cella galvanica lavora reversibilmente ad una P e ad una T costanti, senza effettuare
alcun lavoro eccetto quello elettrico, la variazione di energia libera, che accompagna la reazione di
cella, è data
Lavoro elettrico = w = G = -E z F
( Joule)
dove
E = forza elettromotrice (volt)
F = Faraday = carica trasportata da una mole di elettroni = 96484.6 Coulomb/mole
z = n. di cariche elementari messe in gioco
In realtà una cella, per essere in condizioni di reversibilità, deve avere le seguenti caratteristiche:
1) Se è connessa con una f.e.m. esterna esattamente uguale, ma in opposizione, nella cella non
ha luogo alcun processo;
2) se la f.em. esterna viene diminuita di una quantità infinitesima, la corrente è erogata dalla
cella; se invece la f.e.m. esterna viene aumentata, la corrente attraversa la cella in direzione
opposta. Il processo che si svolge nella cella quando essa stessa eroga corrente, è l’inverso
di quello che si svolge quando assorbe corrente.
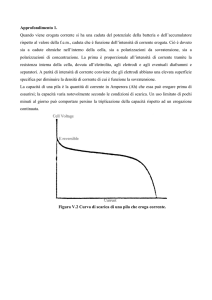
Se riportiamo l’andamento dell’intensità di corrente in funzione della differenza di
potenziale applicata dall’esterno, abbiamo 2 casi possibili:
Osserviamo che sia nel punto A che in quello B, i=0 ( cioè Eesterna = f.e.m. pila), quindi vale la
condizione 1); inoltre in a), se ci spostiamo dalla posizione di equilibrio, verso destra o sinistra,
anche solo di un infinitesimo, osserviamo passaggio di corrente ed in direzioni rispettivamente
opposte (è rispettata la condizione 2). Ciò non accade in b), per cui in questo caso non siamo in
condizioni di reversibilità. Tale condizione si controlla con un potenziometro a compensazione,
denominato potenziometro di Poggendorf, che può essere schematizzato nel seguente modo:
Poiché la f.e.m. Ex da misurarsi è inserita in opposizione alla f.e.m. di alimentazione
(commutatore C in d ), si può trovare, muovendo opportunamente il contatto mobile, un punto
X di AB per il quale non fluisce corrente attraverso il galvanometro G (se spostandoci da X, la
corrente passa in un verso o in un altro, abbiamo trovato la posizione di equilibrio). Per tale
posizione dovrà essere verificata la condizione che la differenza di potenziale fra i punti A e X,
EAX, sia uguale a EX; se i è l’intensità di corrente che percorre il tratto AX ed RAX la resistenza di
tale tratto, avremo che:
EAX =EX = RAX i
Se ora, al posto di EX, si introduce una pila campione la cui f.e.m. è nota ed è uguale a EC, si
ottiene che il galvanometro non segna passaggio di corrente per una posizione X’ tale che:
EAX’ = EC = RAX’ i
Dal rapporto delle 2 relazioni si ottiene:
E X EC
R AX
R AX '
Per cui è sufficiente conoscere Ec e misurare RAX e RAX’ per ricavare la f.em. incognita della pila.
In laboratorio si misura direttamente la f.e.m. della pila utilizzando la seguente tecnica:
1. Nel potenziometro classico di Poggendorf il filo calibrato AB ha una scala tarata in volt.
Dopo aver inserito la pila campione, si sposta il cursore di X sulla tacca corrispondente alla
tensione della pila campione (es. 1.084V), poi si agisce sul cursore di R sino a che il
galvanometro G non segna più passaggio di corrente. In queste condizioni il potenziometro è
tarato per cui, una volta inserita la pila incognita, basterà leggere direttamente la tensione
sulla scala del filo calibrato AB, dopo aver spostato il suo cursore sino a non osservare alcun
passaggio di corrente.
In mancanza di un potenziometro di Poggendorf, è possibile eseguire lo stesso la misura di f.em.
utilizzando un multimetro elettronico ad elevatissima impedenza di ingresso (> di 10 Gohm).
Pur non operando strettamente in condizioni di reversibilità, in quanto il multimetro, pur avendo
una resistenza di ingresso estremamente elevata, quando è connesso, fa passare nella cella una
corrente infinitesimamente piccola, tuttavia il valore misurato è ugualmente preciso.
Una volta ricavata la f.e.m. della pila alle varie temperature, è possibile ricavare le grandezze
termodinamiche G, S e H tramite le seguenti relazioni:
G = - z E F
G
S
T P
E
S zF
T P
H G TS
E
Quindi, per poter ricavare S e H, è necessario conoscere il termine
, denominato
T P
coefficiente termico della pila. Per poter ricavare tale termine, è necessario riportare in un
diagramma la f.e.m E in funzione di T , ottenendo o un andamento di tipo lineare oppure di tipo
parabolico . Nel primo caso basterà applicare la regressione lineare e il coefficiente termico della
pila corrisponderà con la pendenza della retta , b. Nel secondo caso, sarà necessario applicare la
regressione supponendo che l’equazione che soddisfa i dati sia di tipo parabolico
E = a + bT + cT2
E
e il coefficiente termico della pila sarà dato da
=b+2cT.
T P
In questa esperienza viene studiata la termodinamica della pila a bottone ad argento.
E’ un tipo di pila a secco, cioè priva di elementi liquidi, costituita da un anodo formato da una pasta
gelatinosa contenente della polvere di Zn mescolata assieme all’elettrolita KOH e da un catodo
formato da Ag2O mescolato con del carbone, per aumentarne la conduttività.
Il contatto elettrico al catodo viene assicurato utilizzando una lamina metallica di acciaio contenente
del nichel, mentre all’anodo viene usata una lamina di acciaio contenente rame e stagno.
Le reazioni che avvengono agli elettrodi sono le seguenti:
Anodo (-)
Zn(s) + 2 OH-(aq) -> ZnO(s) + H2O(l) + 2e-
Catodo (+)
Ag2O(s) + H2O(l) + 2 e- -> 2 Ag(s) + 2 OH-(aq)
Il processo elettromotore totale risulta pertanto
Zn(s) + Ag2O(s) -> ZnO(s) + 2 Ag(s)
e la f.e.m. dipenderà dalla attività delle specie partecipanti alla reazione mediante la seguente
equazione di Nernst:
RT a ZnO( s ) a Ag ( s )
E E0
ln
zF a Zn ( s ) a Ag 2O ( s )
Essendo tutte le attività unitarie, avremo che E=E°, per cui sarà possibile misurare direttamente
come varia la f.e.m. standard della pila in funzione della temperatura.
Tale pila si presta assai bene a studi termodinamici, in quanto gli elettrodi si comportano in maniera
reversibile (vedi comportamento a) figura precedente) ed inoltre il suo potenziale non dipende
dall’attività delle specie partecipanti alla reazione essendo queste tutte unitarie.
PARTE SPERIMENTALE
APPARECCHIATURA
- 1 pila Zn- Ag2O
- 1 termostato
- 1 multimetro digitale HP34401
- 1 cella per pila Zn-Ag2O
DESCRIZIONE
1. Controllare sul termometro immerso nella vasca che la temperatura del bagno termostatico
sia costante e di circa 25.
2. Inserire la pila nel portacella ed immetterla in un provettone; dopodichè immergere il
provettone nel bagno termostatico e attendere almeno 5 minuti affinché la pila sia ben
termostatata.
3. Connettere il multimetro alla pila assicurandosi che sia stato impostato con una impedenza
di ingresso maggiore di 10 Gohm , in modo da operare in condizioni di corrente pressoché
nulla per leggere correttamente la f.e.m. della pila. Inoltre impostare il n. di cifre a 6.
4. Monitorare la variazione della tensione letta nell’arco di 10 minuti assicurandosi che la
variazione della tensione letta sia inferiore a 2 mV /min. Se è così, annotare il valore della
f.em.
5. Ripetere tutto il processo di misura, dopo aver aumentato la temperatura di 1 grado, sino ad
arrivare a 35°C.
ELABORAZIONE DATI
1) Quantificare l’incertezza sulle misure di f.e.m tenendo presente che l’accuratezza del multimetro
digitale HP34401, utilizzato con un fondo scala di 10V, può essere ricavata mediante la seguente
relazione :
0.004
0.0015
accuratezz a
valore _ letto
10 V
100
100
e l’incertezza tipo, associata a ciascun valore, viene ricavata utilizzando una distribuzione
rettangolare.
2) Applicare la regressione lineare per ricavare la dipendenza da T della f.e.m. e il coefficiente
termico della pila. Quantificare l’incertezza sull’intercetta e sul coefficiente angolare, assumendo un
livello di fiducia del 95%.
3) Ricavare G, S e H a 250C e la relativa incertezza (con un livello di fiducia del 95%).
4) Confrontare i valori ottenuti con quelli tabulati in letteratura.