caricato da
tedescodiego.97
Note per il Corolo Differenziale I per Informatica

Note per il Corso di Calcolo Differenziale I per Informatica
Ernesto De Vito
Dipartimento di Matematica, Università di Genova
Marzo 2018
Avvertenza. Queste note devono servire come guida per lo studio: non sono un libro
di testo (ve ne sono di ottimi da consultare in biblioteca), non sono una trascrizione di
quanto detto a lezione (gli appunti sono essenziali), mancano i commenti ed i disegni
(indispensabili per la comprensione), vi sono alcuni argomenti che non sono stati trattati
a lezione (ma che possono servire di approfondimento). Il simbolo indica punti che
richiedono particolare attenzione.
1. Numeri reali e funzioni
Richiamiamo brevemente alcune notazioni della teoria degli insiemi.
∅
N
Z
Q
R
∈
6∈
⊂
∪
∩
c
\
|
⇒
⇐⇒
∀
∃
6∃
(a, b)
×
insieme vuoto
insieme dei numeri naturali
insieme dei numeri relativi
insieme dei numeri razionali
insieme dei numeri reali
appartiene
non appartiene
inclusione insiemistica
unione insiemistica
intersezione insiemistica
complemento insiemistico
differenza insiemistica
tale che
implica che
se e solo se, equivale
per ogni
esiste
non esiste
coppia ordinata
prodotto cartesiano
Richiamiamo inoltre la definizione di intervallo. Siano a, b ∈ R con a < b.
intervallo limitato aperto
(a, b) = {x ∈ R | a < x < b}
intervallo limitato chiuso
[a, b] = {x ∈ R | a ≤ x ≤ b}
intervallo limitato aperto a destra [a, b) = {x ∈ R | a ≤ x < b}
intervallo limitato aperto a sinistra (a, b] = {x ∈ R | a < x ≤ b}
intervallo illimitato aperto a destra (−∞, b) = {x ∈ R | x < b}
intervallo illimitato chiuso a destra
(−∞, b] = {x ∈ R | x ≤ b}
intervallo illimitato aperto a sinistra (a, +∞) = {x ∈ R | x > a}
intervallo illimitato chiuso a sinistra [a, +∞) = {x ∈ R | x ≥ a}
.
La stessa notazione (a, b) è usata per indicare sia la coppia ordinata sia l’intervallo
aperto di estremi a e b.
1
2
2. I numeri
I numeri naturali. L’insieme dei numeri naturali N è formato da tutti i numeri interi
positivi, compreso lo 0,
N = {0, 1, 2, . . .},
con una relazione d’ordine
⇐⇒
n<m
n è più piccolo di m.
Tra due numeri naturali sono definite due operazioni:
a) la somma +
∀n, m ∈ N
⇒
n + m = m + n ∈ N,
rispetto cui 0 è l’elemento neutro
∀n ∈ N
⇒
n + 0 = n,
b) il prodotto ·
∀n, m ∈ N
⇒
n · m = m · n ∈ N,
rispetto cui 1 è l’elemento neutro
∀n ∈ N
⇒
n · 1 = n.
Il prodotto di un numero n per se stesso, ripetuto m volte, si indica con
nm = n
· . . . · n}
| · n {z
con la convenzione che
n0 = 1,
m volte
e si legge n elevato ad m (n è la base ed m l’esponente).
I numeri relativi. L’insieme dei numeri relativi è formato dai numeri interi positivi, nulli
o negativi
Z = {0, ±1, ±2, . . . , }.
Anche in Z sono definite una relazione d’ordine (<) e le operazione di somma (+) e prodotto
(·). Per la somma vale la seguente proprietà (esistenza dell’opposto)
∀n ∈ Z ∃ unico m ∈ Z tale che n + m = 0,
il numero m è detto opposto e si denota con −n.
I numeri razionali. L’insiemi dei numeri razionali è definito come
n
Q = { | n ∈ Z, m ∈ N, m 6= 0},
m
0
n
n
0
0
dove due frazioni m
e m
0 identificano lo stesso numero razionale se n · m = n · m. Anche
in Q sono definite una relazione d’ordine (<) e le operazione di somma (+) e prodotto (·).
Per il prodotto vale la seguente proprietà (esistenza del reciproco)
∀q ∈ Q, q 6= 0 ∃ unico t ∈ Q tale che q · t = 1,
il numero t è detto reciproco e si denota con
1
q
oppure q −1 .
Numeri reali. L’insieme dei numerali reali si identifica con i punti di una retta orientata
in cui è stata scelta un’origine (identificata con 0) ed un’unità di misura in modo tale che il
punto della semiretta di destra che dista 1 dall’origine è identificato con il punto 1. Inoltre
vale che
N ⊂ Z ⊂ Q ⊂ R.
In R sono definite le usuali operazioni di somma e prodotto ed una relazione d’ordine
(x < y se il punto x è a sinistra di y).
3
3. Le funzioni
La definizione di funzione è uno dei concetti fondamentali della matematica. In particolare
saranno studiate le funzioni reali di variabile reale.
Definizione 1. Una funzione (reale di variabile reale) f : A → R con A ⊂ R è una legge
che assegna ad ogni elemento x ∈ A un unico valore y = f (x) ∈ R. L’insieme A è detto
dominio di f e denotato anche con dom f .
Si chiama grafico di f il sottoinsieme del piano cartesiano definito dall’equazione y = f (x)
{(x, y) ∈ R2 | y = f (x), x ∈ A}.
Si chiama immagine di f l’insieme di valori effettivamente presi dalla funzione e si denota
con Im f
Im f = {f (x) ∈ R | x ∈ A}.
Le precedenti definizioni hanno la seguente interpretazione geometrica. Ricordiamo che le
rette parallele all’asse delle ascisse (asse x) hanno equazione y = y0 , mentre quelle parallele
all’asse delle ordinate (asse y) hanno equazione x = x0 .
a) Il grafico di f è una curva nel piano caratterizzata dal fatto che, dato x0 ∈ A, la retta
x = x0 , parallela all’asse delle ordinate, interseca il grafico di f in un solo punto P0 le
cui coordinate sono P0 = (x0 , f (x0 )).
Vi sono curve del piano che non sono il grafico di alcuna funzione.
b) Un punto P0 = (x0 , y0 ) sta sul grafico di f se e solo se x0 ∈ A e y0 = f (x0 ).
c) Il dominio A della funzione è un sottoinsieme dell’asse delle ascisse ed è la proiezione
del grafico della funzione su tale asse.
d) L’immagine Im f è un sottoinsieme dell’asse delle ordinate, costituito da tutti i valori
y0 ∈ R per cui la retta y = y0 , parallela all’asse delle ascisse, interseca il grafico di f
in almeno un punto, cioé Im f è la proiezione del grafico della funzione sull’asse delle
ordinate.
Definizione 2. Una funzione f : A → R, y = f (x), è detta
a) iniettiva se per ogni y0 ∈ R l’equazione y0 = f (x) ammette al più una soluzione;
b) surgettiva se per ogni y0 ∈ R l’equazione y0 = f (x) ammette almeno una soluzione;
c) bigettiva se per ogni y0 ∈ R l’equazione y0 = f (x) ammette una ed una sola soluzione.
Dal punto di vista geometrico l’equazione y0 = f (x) equivale a trovare le intersezioni tra
il grafico y = f (x) e la retta y = y0 parallela all’asse delle ascisse
(
y = f (x)
y0 = f (x)
⇐⇒
.
y = y0
Ne segue che
a) Una funzione è iniettiva se ogni retta y = y0 , parallela all’asse delle ascisse, interseca il
grafico di f in al più un punto;
b) una funzione è surgettiva se ogni retta y = y0 , parallela all’asse delle ascisse, interseca
il grafico di f in almeno un punto;
c) una funzione è bigettiva se ogni retta y = y0 , parallela all’asse delle ascisse, interseca il
grafico di f in esattamente un punto.
Valgono, inoltre, le seguenti condizioni equivalenti.
a)
b)
c)
d)
f
f
f
f
è
è
è
è
iniettiva se e solo se dati x1 , x2 ∈ A tali che f (x1 ) = f (x2 ), allora allora x1 = x2 ;
iniettiva se e solo se dati x1 , x2 ∈ A tali che x1 6= x2 allora f (x1 ) 6= f (x2 );
surgettiva se e solo se l’immagine di f è tutto R, cioè Im f = R;
bigettiva se e solo se f è sia iniettiva sia surgettiva.
4
Definizione 3. Una funzione f : A → R è detta
a) crescente se per ogni x1 , x2 ∈ A tali che x1 ≤ x2 , allora
f (x1 ) ≤ f (x2 );
b) decrescente se per ogni x1 , x2 ∈ A tali che x1 ≤ x2 , allora
f (x1 ) ≥ f (x2 );
c) strettamente crescente se per ogni x1 , x2 ∈ A tali che x1 < x2 , allora
f (x1 ) < f (x2 );
d) decrescente se per ogni x1 , x2 ∈ A tali che x1 < x2 , allora
f (x1 ) > f (x2 ).
Una funzione crescente o decrescente è detta monotona.
Definizione 4. Una funzione f : A → R è detta
a) pari se per ogni x ∈ A, allora −x ∈ A e f (−x) = f (x);
b) dispari se per ogni x ∈ A, allora −x ∈ A e f (−x) = −f (x).
Una funzione è pari se il suo grafico è simmetrico rispetto all’asse delle ordinate, mentre è
dispari se il suo grafico è simmetrico rispetto all’origine.
I seguenti esempi illustrano le precedenti definizioni.
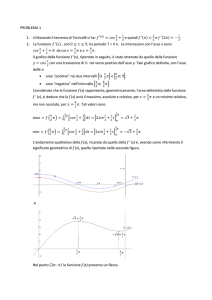
Esempio 1. Sia f (x) = (x − 1)2 . Il suo dominio è R ed il suo grafico è
{(x, y) ∈ R2 | y = (x − 1)2 },
cioé la parabola di vertice (1, 0) ed asse parallelo all’asse delle ordinate (curva blu in
Figura 1). Proiettando la parabola su tale asse si vede che l’immagine di f è l’insieme
[0, +∞). La funzione non è iniettiva (ad esempio la retta y = 1 interseca il grafico in due
punti), né surgettiva (ad esempio la retta y = −1 non interseca il grafico di f ). La funzione
non è né pari né dispari.
Esempio 2. Sia f (x) = x1 . Il suo dominio è
dom f = {x ∈ R | x 6= 0} = (−∞, 0) ∪ (0, +∞) = R \ {0}.
Il grafico di f è
1
e x 6= 0} = {(x, y) ∈ R2 | xy = 1},
x
cioé l’iperbole equilatera, i cui asintoti sono gli assi cartesiani (curva verde in Figura 1).
Proiettando tale iperbole sull’asse delle ordinate si vede che l’immagine di f è l’insieme
(−∞, 0) ∪ (0, +∞). La funzione è iniettiva, ma non surgettiva (tutte le rette parallele
all’asse delle ascisse intersecano il grafico in un solo punto, tranne la retta y = 0 che non
ha intersezione). La funzione è dispari, poiché il grafico è simmetrico rispetto all’origine.
√
Esempio 3. Sia f (x) = 1 − x2 . Il suo dominio è
{(x, y) ∈ R2 | y =
dom f = {x ∈ R | 1 − x2 ≥ 0} = [−1, 1].
Il grafico di f è
{(x, y) ∈ R2 | y =
p
1 − x2 } = {(x, y) ∈ R2 | y ≥ 0 e x2 + y 2 = 1},
cioé la semi-circonferenza di centro (0, 0), raggio 1, che sta nel piano positivo delle y (curva
rossa in Figura 1). Proiettando tale semi-circonferenza sull’asse delle ordinate si vede che
l’immagine di f è l’intervallo [0, 1]. La funzione non è iniettiva (infatti la retta y = 0
interseca il grafico in due punti) e non è surgettiva (la retta y = 2 non interseca mai il
grafico). La funzione è pari, poiché il grafico è simmetrico rispetto all’asse delle ordinate.
5
Figura 1. Grafici relativi
agli Esempi 1,2,3.
Figura 2. Grafico relativo
all’Esempio 4.
Il seguente esempio mostra come si possano definire funzioni combinando insieme diverse
leggi.
Esempio 4. Sia f : R → R la funzione definita da
(
f (x) =
1
x
(x −
1)2
x<0
.
x≥0
Il dominio di f è tutto R, il grafico di f è l’unione di due archi di curve: l’arco di iperbole
equilatera nel semi-piano negativo delle ascisse e l’arco di parabola nel semi-piano positivo
delle ascisse1 (curva blu in Figura 2)
{(x, y) ∈ R2 | x < 0 e xy = 1} ∪ {(x, y) ∈ R2 | x ≥ 0 e y = (x − 1)2 }.
Proiettando il grafico sull’asse delle ordinate, si vede che Im f = R, per cui la funzione è
surgettiva, ma non è iniettiva (la retta y = 1 interseca il grafico in due punti). La funzione
non è né pari né dispari.
3.1. Operazioni tra funzioni. Tra le funzioni, sono definite alcune operazioni che permettono di costruire nuove funzioni. Richiamo le principali.
1L’unione dell’intera iperbole e dell’intera parabola non è il grafico di alcuna funzione, poiché ad esempio
la retta x = 1 interseca l’insieme cosí ottenuto in due punti.
6
Definizione 5 (Funzione composta). Date due funzione f : A → R, y = f (x), e g : B → R,
z = g(y) tali che
per ogni x ∈ A allora f (x) ∈ B
⇐⇒
Im f ⊂ dom g
la funzione
g◦f :A→R
(g ◦ f )(x) = g(f (x)) x ∈ A,
si chiama funzione composta di f con g.
La condizione che l’immagine di f sia contenuta nel dominio di g è necessaria affinché si
posso calcolare il valore di g(y) nel punto y = f (x). Il risultato della composizione di due
funzioni dipende dall’ordine, per cui in generale g(f (x)) 6= f (g(x)).
√
Esempio 5. Siano f (x) = x e g(x) = x + 1, allora
√
g(f (x)) = x + 1
dom g ◦ f = [0, +∞)
f (g(x)) =
Siano f (x) =
√
√
dom f ◦ g = [−1, +∞).
x+1
x e g(x) = x2 , allora
dom g ◦ f = [0, +∞)
g(f (x)) = x
(
x
x≥0
f (g(x)) =
−x x < 0
dom f ◦ g = R.
Definizione 6 (Funzione inversa). Data una funzione f : A → R, y = f (x) iniettiva, la
funzione che assegna ad ogni y ∈ Im f l’unico x ∈ A tale che f (x) = y. si chiama funzione
inversa e si denota con
f −1 : B → R
x = f −1 (y)
dove B = Im f .
Il dominio della funzione inversa è precisamente l’immagine di f , poiché se y 6∈ Im f
l’equazione y = f (x) non ha soluzione. La condizione che la funzione f sia iniettiva è
necessaria per assicurare che, dato y ∈ Im f , l’equazione y = f (x) ammetta un’unica
soluzione. Ne segue che l’immagine di f −1 è il dominio di f . Riassumendo
dom f −1 = Im f
e
Im f −1 = dom f
f −1 (f (x)) = x
e
f (f −1 (y)) = y.
Nel definire la funzione inversa è utile usare la lettera y per indicare la variabile indipendente, x = f −1 (y), tuttavia quando si vuole disegnare il grafico di f −1 occorre scambiare
la x con la y (per convenzione la variabile indipendente corrisponde ai punti dell’asse delle
ascisse). Ne segue che il grafico della funzione inversa f −1 è il simmetrico del grafico di f
rispetto alla bisettrice del primo e terzo quadrante, la retta y = x.
.
Data una funzione f : A → R
f (x)−1 =
1
f (x)
denota il reciproco purché x ∈ A e f (x) 6= 0, mentre
f −1 (x)
denota il valore della funzione inversa purché f sia iniettiva e x ∈ dom f −1 = Im f .
Osserviamo che
f (x)f (x)−1 = 1
f (f (x)−1 ) = x.
7
Figura 3. Grafici delle funzioni dell’Esempio 6.
√
2x − 1 con dom f = [1/2, +∞). Dato y ∈ R studio l’equazione
√
1
y = f (x)
⇐⇒
y = 2x − 1 con x ≥ .
2
Se y < 0 l’equazione non ha alcuna soluzione (la retta parallela all’asse delle y non ha
2
intersezione con il grafico di f ), se y ≥ 0, l’equazione ha un’unica soluzione x = y 2+1 .
Per cui l’immagine di f è [0, +∞) e la funzione è iniettiva. È quindi possibile definire la
funzione inversa, che è data da2
Esempio 6. Sia f (x) =
x2 + 1
x ∈ [0, ∞) = dom f −1 ,
2
il cui grafico è l’arco di parabola con asse l’asse delle ordinate, vertice (0, 21 ) e che giace nel
piano positivo delle x. Il grafico di f si ottiene facendo il simmetrico rispetto alla bisettrice
y = x (vedi Figura 3).
f −1 (x) =
Definizione 7 (Traslazioni
della funzione
y = f (x + a)
y = f (x − a)
y = f (x) + a
y = f (x) − a
e dilatazioni). Data una funzione y = f (x) ed a > 0, il grafico
si
si
si
si
y = f (ax)
si
y = af (x)
si
y = f (−x)
y = −f (x)
y = −f (−x)
si
si
si
ottiene traslando a sinistra
ottiene traslando a destra
ottiene traslando in alto
ottiene (
traslando in basso
contraendo lungo l’asse x se a > 1
ottiene
dilatando lungo l’asse x
se 0 < a < 1
(
contraendo lungo l’asse y se 0 < a < 1
ottiene
dilatando lungo l’asse y
se a > 1
ottiene riflettendo rispetto all’asse y
ottiene riflettendo rispetto all’asse x
ottiene riflettendo rispetto all’origine
il grafico di f .
Nel seguito richiamo le principali proprietà di alcune funzioni di uso frequente.
2La x e la y sono state scambiate.
8
Figura 4. Grafici di alcune potenze.
3.2. Potenze. Richiamo brevemente le principali proprietà delle funzioni potenze.
x0 = 1
x∈R
(
−xn
(−x)n =
xn
x−n = x1n
√
1
xn = n x
√
xq = ( m x)n
n = 1, 3, 5, . . .
n = 2, 4, 6, . . .
x
( 6= 0 n ∈ N
x∈R
n dispari
x ∈ [0, +∞) n pari
n
q=m
∈ Q con m > 0, x > 0
Con la convenzione che x0 = 1 per ogni x ∈ R, vale l’uguaglianza 00 = 0. Questa è
una convenzione che non è adottata in tutti i libri.
.
Richiamiamo alcune proprietà delle potenze.
xa+b = xa xb
(xa )b = xab
xa1 < xa2
xa1 < xa2
x > 0 e a, b ∈ R
x > 0 e a, b ∈ R
0 < x1 < x2 e a > 0
0 < x1 < x2 e a < 0
Nella Figura 4 sono riportati i grafici di y = xa con a = 1, 2, 3, −1, −2, 1/2 ed 1/3.
3.3. Funzione esponenziale. Richiamiamo brevemente le principali proprietà della funzione esponenziale. La base a è un numero reale strettamente positivo con a 6= 1. Il
9
Figura 5. Grafici di alcuni esponenziali.
dominio della funzione esponenziale è R e la sua immagine è (0, +∞).
a0 = 1
ax1 +x2 = ax1 ax2
x
a−x = a1
(ax )b = abx
(
ax1 < ax2
ax1 > ax2
x1 , x2 ∈ R
x∈R
x, b ∈ R
0 < x1 < x2 e a > 1
0 < x1 < x2 e 0 < a < 1
Se si sceglie come base il numero di Nepero e, la funzione esponenziale si denota anche con
exp x. Nella Figura 5 sono riportati i grafici di y = ax con a = 2, e, 3, 1/2, 1/e ed 1/3.
3.4. Funzione logaritmo. Richiamiamo brevemente le principali proprietà della funzione
logaritmo. Ricordo che loga x è la funzione inversa della funzione esponenziale ax , dove
la base a è un numero reale strettamente positivo con a 6= 1. Il dominio del logaritmo è
l’intervallo (0, +∞) e la sua immagine è R.
loga ax = x
aloga x = x
loga 1 = 0
x∈R
x>0
loga (x1 x2 ) = loga x1 + loga x2
loga xb = b loga x
x > 0, b ∈ R
loga x
logb x =
x > 0 e b > 0 b 6= 1
loga b
(
loga x1 < loga x2
se 0 < x1 < x2 e a > 1
loga x1 > loga x2
se 0 < x1 < x2 e 0 < a < 1
Se si sceglie come base il numero di Nepero e, il logaritmo si denota semplice con log x
oppure ln x. Nella Figura 6 sono riportati i grafici di y = loga x con a = 2, e, 3, 1/2, 1/e ed
1/3.
10
Figura 6. Grafici di alcuni logaritmi.
3.5. Funzioni trigonometriche. Richiamiamo brevemente le principali proprietà delle
funzioni trigonometriche (gli angoli sono espressi in radianti).
sin(x + 2π) = sin x
sin(−x) = − sin x
cos(x + 2π) = cos x
cos(−x) = cos x
tan(x + π) = tan x
tan(−x) = − tan x
x 6=
π
+ kπ k ∈ Z
2
π
π
≤ x1 < x2 ≤
2
2
cos x1 > cos x2
0 ≤ x1 < x2 ≤ π
π
π
tan x1 < tan x2
− < x1 < x2 <
2
2
2
2
1 = sin x + cos x
teorema di Pitagora
sin x
π
tan x =
x 6= + kπ k ∈ Z
cosx
2
π
π
−x
sin x = cos
−x
cos x = sin
2
2
sin(x1 + x2 ) = sin x1 cos x2 + cos x1 sin x2
formula di somma
sin x1 < sin x2
−
cos(x1 + x2 ) = cos x1 cos x2 − sin x1 sin x2
sin(2x) = 2 sin x cos x
2
formula di somma
formula di duplicazione
2
cos(2x) = cos x − sin x
formula di duplicazione
r
x
1 − cos x
sin =
0 ≤ x ≤ 2π
formula di bisezione
2
2
r
x
1 + cos x
−π ≤x≤π
formula di bisezione
cos =
2
2
Nella Figura 7 sono riportati i grafici dell tre funzioni trigonometriche.
3.6. Funzioni trigonometriche inverse. Richiamo brevemente le principali proprietà
delle funzioni trigonometriche inverse. Ricordo che arcsin x è la funzione inversa della
funzione sin x ristretta all’intervallo [−π/2, π/2], mentre arccos x è la funzione inversa della
11
Figura 7. Grafici delle funzioni trigonometriche.
funzione cos x ristretta all’intervallo [0, π]. In entrambi i casi il dominio è l’intervallo [−1, 1],
mentre l’immagine di arcsin x è [−π/2, π/2], mentre quella di arccos x è [0, π]. Infine,
arctan x è la funzione inversa della funzione tan x ristretta all’intervallo (−π/2, π/2), il
dominio è l’intervallo R e l’immagine è l’intervallo (−π/2, π/2).
sin(arcsin x) = x
π
π
≤x≤
2
2
−1≤x≤1
arccos(cos x) = x
0 ≤ x1 ≤ π
cos(arccos x) = x
−1≤x≤1
π
π
− <x<
2
2
x∈R
arcsin(sin x) = x
arctan(tan x) = x
tan(arctan x) = x
−
arcsin(−x) = − arcsin x
−1≤x≤1
arctan(−x) = − arctan x
x∈R
arcsin x1 < arcsin x2
− 1 ≤ x1 < x2 ≤ 1
arccos x1 > arccos x2
− 1 ≤ x1 < x2 ≤ 1
arctan x1 < arctan x2
x1 < x2
Nella Figure 8 e 9 sono riportati i grafici delle funzioni trigonometriche inverse.
3.7. Modulo. La funzione modulo o valore assoluto è definita da
(
x
se x ≥ 0
|x| =
x ∈ R,
−x se x < 0
12
Figura 8. Grafici dell’arcoseno e arcocoseno.
Figura 9. Grafico dell’arcotangente.
il dominio è R, l’immagine è l’intervallo [0, +∞) e il suo grafico è rappresentato in Figura 10.
Nella tabella 1 sono riassunti il dominio e l’immagine delle funzioni appena introdotte.
13
Figura 10. Grafici della funzione modulo.
dom f = R
dom f = R
dom f = {x ∈ R | x 6= π/2 + kπ | k ∈ Z}
dom f = [−1, 1]
dom f = [−1, 1]
dom f = R
dom f = R
y = sin x
y = cos x
y = tan x
y = arcsin x
y = arccos x
y = arctan x
y = |x|
dom f = R
dom f = (0, +∞)
con a > 0, a 6= 1
a = 1, 2, 3, . . .
a = −1, −2, −3, . . .
a = n1 n = 1, 3, 5, . . .
a = n1 n = 2, 4, 6, . . .
altri casi
y = loga x con a > 0, a 6= 1
y=
ax
y = xa
R
R \ {0}
R
[0, +∞)
(0, +∞)
dom f
Im f = R
Im f = (0, ∞)
Im f
a = 1, 3, 5, . . .
a = 2, 4, 6, . . .
a = −1, −3, −5, . . .
a = −2, −4, −6, . . .
a = n1 n = 1, 3, 5, . . .
a = n1 n = 2, 4, 6, . . .
altri casi
Im f = [−1, 1]
Im f = [−1, 1]
Im f = R
Im f = [−π/2, π/2]
Im f = [0, π]
Im f = (−π/2, π/2)
Im f = [0, +∞)
R
[0, +∞]
R \ {0}
(0, +∞)
R
[0, +∞)
(0, +∞)
(
abA1
base a
EXP(A1) base e
base e
LN(A1)
LOG10(A1) base 10
LOG(A1; a) base a
SEN(A1)
COS(A1)
TAN(A1)
ARCSEN(A1)
ARCCOS(A1)
ARCTAN(A1)
ASS(A1)
A1ba
COMANDO EXCEL
Tabella 1. Alcune funzioni elementari. Per le funzioni trigonometriche gli angoli sono espressi in radianti. Per i comandi Excel si
suppone che il valore della x sia memorizzato nella cella A1
seno
coseno
tangente
arcoseno
arcocoseno
arcotangente
modulo
logaritmo
esponenziale
potenze
y = f (x)
14
15
E-mail address: [email protected]