PROBLEMA 1
1. Utilizzando il teorema di Torricelli si ha:
2. La funzione
, con
da cui
e quindi
e
.
, ha periodo T = 4 . Le intersezioni con l’asse x sono:
e
.
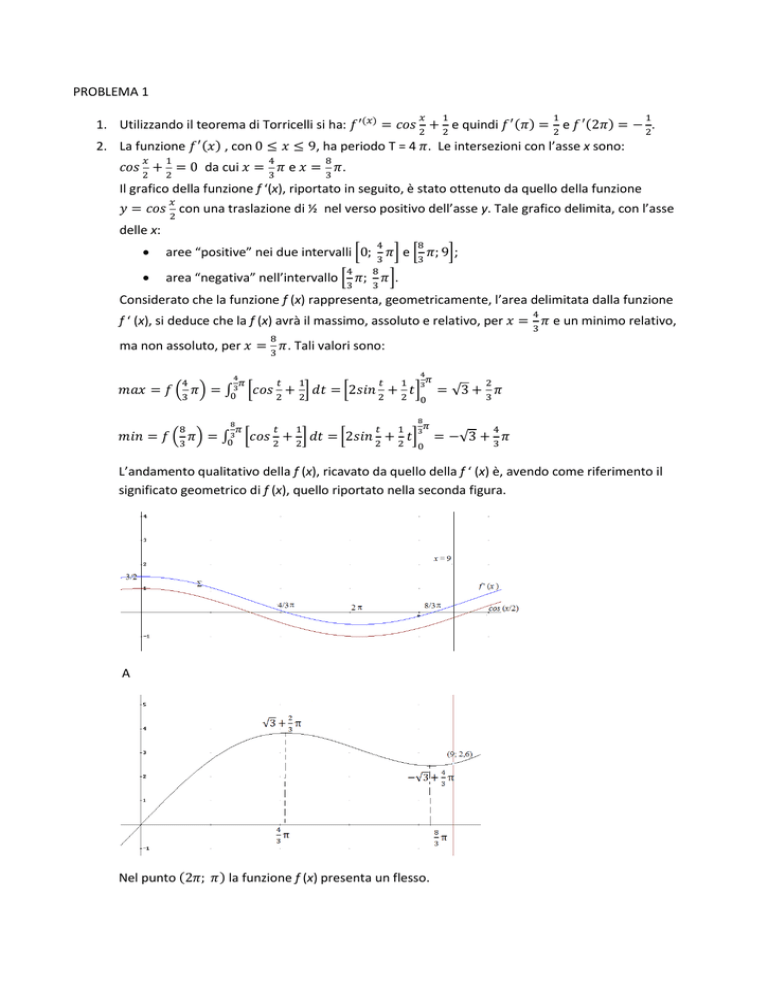
Il grafico della funzione f ‘(x), riportato in seguito, è stato ottenuto da quello della funzione
con una traslazione di ½ nel verso positivo dell’asse y. Tale grafico delimita, con l’asse
delle x:
aree “positive” nei due intervalli
area “negativa” nell’intervallo
e
;
.
Considerato che la funzione f (x) rappresenta, geometricamente, l’area delimitata dalla funzione
f ‘ (x), si deduce che la f (x) avrà il massimo, assoluto e relativo, per
ma non assoluto, per
e un minimo relativo,
. Tali valori sono:
L’andamento qualitativo della f (x), ricavato da quello della f ‘ (x) è, avendo come riferimento il
significato geometrico di f (x), quello riportato nella seconda figura.
A
Nel punto
la funzione f (x) presenta un flesso.
Nella costruzione del secondo grafico si è tenuto conto dei valori assunti dalla funzione f(x) in
che valgono, rispettivamente,
3. Il valore medio richiesto vale:
4. Il volume richiesto è:
.PROBLEMA 2
1. La funzione f(x) è definita su tutto l’asse reale e risulta ovunque positiva (tali sono, per ogni x, il
numeratore e il denominatore.
Poiché risulta
, essa ha per asintoto orizzontale l’asse delle ascisse y = 0 e non
ha altri asintoti.
E’ una funzione pari e, pertanto,simmetrica rispetto all’asse y.
Dallo studio del segno della derivata prima si ha:
e, pertanto, la funzione ha un massimo nel punto R (0; 2).
Dallo studio del segno della derivata seconda si ha:
e, pertanto, si hanno due flessi nei punti
Si ha il seguente grafico
,
.
Poiché si ha f’(-2)=1/2 e f ‘(2)= -1/2, le tangenti nei punti P e Q hanno, rispettivamente, equazioni
y=(1/2)x+2 e y=(-1/2)x+2. Tali rette si intersecano in R=(0; 2).
Dalle coordinate dei punti si evince che le diagonali del quadrilatero OPQR sono perpendicolari e e
si bisecano nel punto H=(0; 1). Ciò è sufficiente per concludere che PQRS è un rombo.
Con riferimento al grafico si ha
, pertanto
Gli altri due angoli hanno misure supplementari a quella di
.
.
2. Ricaviamo i punti A e B risolvendo i sistemi:
le cui soluzioni sono
Affinché il punto
,
appartenga al grafico , le sue coordinate devono soddisfare
l’equazione della funzione f. Infatti risulta
.
3. Si ha:
Tale valore è anche l’area di
un cerchio di raggio 1.
Indicata con T la regione di cui si chiede l’area, si ha, per simmetria,
.
4. Dovendo integrare rispetto alla variabile y occorrerà invertire la funzione f ottenendo,
limitatamente al ramo x>0, la funzione
all’integrale
. Il volume W si ottiene sommando
il volume del cilindro di altezza OH e raggio di base OK.
QUESTIONARIO
1. Indicata con
la misura del terzo lato, e con
il semiperimetro per la formula di Erone si ha:
e, sostituendo in
le misure 2, 3 degli altri due lati, si ottiene
, da cui l’equazione risolvente
della condizione
, ovvero
, il terzo lato misura
. Tendo conto
.
2. Le condizioni di realtà impongono:
Tale sistema è equivalente alle seguenti condizioni:
a sua volta equivalente a
3. Si tratta della retta passante per
e perpendicolare alla retta
assegnate, il coefficiente angolare della retta
ha equazione
. Si ha infine
, ovvero
.
. Tenendo conto delle coordinate
è
e, pertanto, la retta richiesta
.
4. Il tronco di piramide ABCDSPQR appartiene alla piramide ABCDV. Intersecando la piramide con il
piano per V e per i punti medi MN di due lati opposti della base si ha il triangolo isoscele VMN,
simile e complanare al triangolo VFG, i cui vertici F, G sono i punti medi dei due lati della base
minore del tronco di piramide, corrispondenti ai punti medi M, N.
Con riferimento alla figura si ha PQ=h, AB=a, FG=b.
Sfruttando la similitudine fra i triangoli VMN e VFG si ha: VO: VP = MN : FG, cioè (VP+h) : VP = a :
b , da cui segue, per la proprietà dello scomporre, h : VP = (a-b) : b e, infine
.
Il tronco di piramide è dato dalla differenza delle due piramidi di rispettive altezze VO=VP+h e VP, il
suo volume è pertanto ottenuto come segue:
5. Indicate con a, b, c le tre dimensioni della valigia più piccola, avente quindi volume
tre dimensioni vengono aumentate del:
10% il nuovo volume sarà
;
20% il nuovo volume sarà
;
25% il nuovo volume sarà
.
, se le
Pertanto gli aumenti percentuali dei volumi saranno rispettivamente 33,1%, 72,8% e 95,3%.
6. Il più piccolo numero ottenibile è 1234567. I sei numeri più piccoli si ottengono dal più piccolo
permutando le ultime tre cifre, 5, 6, 7, essendo 6 le permutazioni di tre oggetti. Pertanto il settimo
numero in ordine crescente si ottiene dal più piccolo scambiando di posto le cifre 4 e 5, cioè
1235467.
I 720 numeri più piccoli si ottengono dal primo permutando le ultime 6 cifre 2, 3, 4, 5, 6, 7, essendo
proprio 720 il delle permutazioni di 6 oggetti. Pertanto il 721 numero più piccolo si otterrà dal più
piccolo scambiando di posto le cifre 1 e 2, cioè 2134567.
7. La similitudine tra il rettangolo intero e la sua metà impone:
ovvero
La condizione sull’area del rettangolo impone
da cui risulta
e
.
8. L’area del triangolo situato nel semipiano positivo delle y vale 2, mentre quella del triangolo
situato nel semipiano negativo delle y vale 1. Pertanto la funzione area g (x) avrà andamento
crescente, dal valore 0 al valore massimo 2, quando x varia tra 0 e 2 e andamento decrescente, dal
valore 2 al valore 1, quando x varia tra 2 e 4. Dopo 4 la funzione riprende a crescere, pertanto nel
valore x = 4 si ha un minimo per la g (x).
9. Si ha:
, utilizzando il limite notevole
.
10. Il grafico di f ‘(x) è il grafico A). Infatti la funzione data, crescente all’esterno dell’intervallo (-2; 2) e
crescente al suo interno, deve avere derivata positiva all’esterno del suddetto intervallo, negativi al
suo interno, nulli agli estremi -2 e 2 , valori per i quali la funzione assegnata presenta,
rispettivamente, massimo e minimo. L’unica funzione f ‘ (x) che rispetta le suddette condizioni e
quella corrispondente al primo grafico.
GIANFRANCO PISTONI ROHR FERRUCCIO