Limiti: Caso 1

Limiti: Caso 1
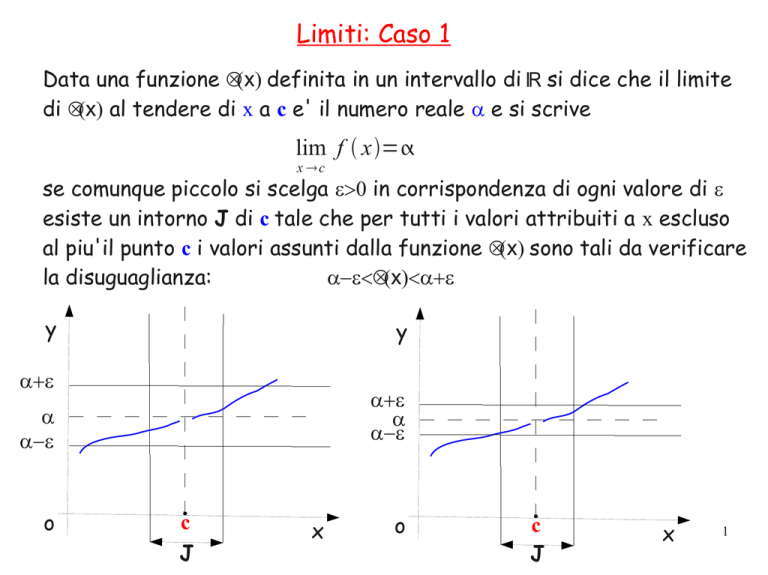
Data una funzione ƒ(x) definita in un intervallo di ℝ si dice che il limite
di ƒ(x) al tendere di x a c e' il numero reale α e si scrive
lim f  x=
x c
se comunque piccolo si scelga ε>0 in corrispondenza di ogni valore di ε
esiste un intorno J di c tale che per tutti i valori attribuiti a x escluso
al piu'il punto c i valori assunti dalla funzione ƒ(x) sono tali da verificare
la disuguaglianza:
α−ε<ƒ(x)<α+ε
y
y
α+ε
α+ε
α
α−ε
α
α−ε
o
c
J
x
o
c
J
x
1
Limite di una funzione continua:
Se abbiamo una funzione continua: lim f  x = f c
xc
cioe' il limite per x che tende al valore c della funzione ƒ(x) e' il
valore ƒ(c) che la funzione assume in c
Esempi:
lim e x =e0 =1
x 0
lim 3x−1=3⋅1−1=2
x 1
Se la funzione non e' continua caso per caso si deve calcolare il limite
se esiste.
2
Limiti: Caso 2
Una funzione ƒ(x) definita in un intervallo di ℝ ha per limite infinito
positivo o l'infinito negativo per x che tende c e si scrive
lim f  x =∞
lim f  x =−∞
xc
xc
se scelto M arbitrariamente grande esiste un intorno di c, J tale che
per tutti i valori attribuiti a x escluso al piu'il punto c la funzione
assuma valori: ƒ(x)>M o rispettivamente ƒ(x)<−M
y
M
o
/\/\
/\/\
y
c
J
x
-M
o
c
J
x
3
Esempi:
x
lim
=∞
x 1 x−1
lim tan  x=∞
x  /2
In particolare per la tangente di un angolo dobbiamo specificare se
tende a π/2 da sinistra o da destra. Infatti:
lim tan  x =∞
x / 2-
lim tan  x =−∞
x / 2+
4
Limiti: Caso 3
Una funzione ƒ(x) definita in un campo di esistenza ℝ illimitato a
destra o sinistra ha per limite un numero reale α per x che tende a ±∞
e si scrive
lim f  x=
lim f  x= e/o
x −∞
x ∞
se comunque piccolo si scelga ε>0 in corrispondenza di ogni valore di ε
esiste un numero reale K tale che attribuendo a x valori x>K o x<-K
i valori assunti dalla funzione ƒ(x) sono tali da verificare la
disuguaglianza:
α−ε<ƒ(x)<α+ε
y
y
α+ε
α+ε
α
α−ε
α
α−ε
o
/\/\
K
x
o
-K
/\/\
x
5
Esempi:
2x−1 2x
lim
= =2
x
x ∞ x1
lim e x =0
x −∞
1 1
lim e = lim x = =0
∞
x ∞
x ∞ e
−x
6
Limiti: Caso 4
Una funzione ƒ(x) definita in un campo di esistenza ℝ illimitato a
destra o sinistra si dice che per x che tende a ±∞ ha per limite infinito
positivo o negativo e si scrive
lim f  x=±∞ lim f  x=±∞
x ∞
x −∞
se in corrispondenza di un numero M arbitrariamente grande esiste un
numero reale K tale che attribuendo a x valori x>K o x<-K
la funzione assume valori ƒ(x)>M o rispettivamente ƒ(x)<−M
y
/\/\
/\/\
/\/\
-M
K
x
/\/\
-K
o
/\/\
o
M
/\/\
M
y
x
-M
7
Esempi:
+∞
y
+∞
lim x=∞
x ∞
lim x=−∞
x
x −∞
-∞
-∞
lim −x=−∞
x ∞
lim x=∞
-∞
+∞
y
x −∞
x
-∞
+∞
8
Esempi di calcolo di limiti:
1) Funzione che si dimostra essere continua
x 2−9
f  x =
x−3
x 2 −9
lim
x 3 x−3
Definita su ℝ eccetto x=3. Cosa possiamo dire
Per x=3?
Se si sostituisce x=3 otteniamo 0/0 forma indeterminata
Per studiare il comportamento delle funzione in 3 osserviamo che:
x 2 −9  x −3 x3
=
=x3 si considera questa come nuova funzione
x−3
x−3
che approssima la nostra funzione in x=3
x 2 −9
lim
=lim  x3=6
x 3 x−3
x 3
Quindi la funzione per x=3 e' continua e il suo valore e' 6
9
Esempi di calcolo di limiti:
2) Calcolo degli asintoti
x 2 1
f  x =
2x−1
Definita su ℝ eccetto x=1/2. Cosa possiamo dire
per x=1/2?
x 2 1
lim
=∞ In questo caso il limite destro e sinistro non sono uguali
x 1/ 2 2x−1
x 21
lim
=−∞
x 1/2- 2x−1
Se mi avvicino a ½ da sinistra ho valori inferiori a
½ quindi χ≤1 che significa “0 negativo”
x 21
lim
=∞
x 1/2+2x−1
Se mi avvicino a ½ da destra ho valori superiori a
½ quindi χ≥1 che significa “0 positivo”
Quindi x=1/2 e' un asintoto verticale
y
o
x
10
Esercizi
1) Calcolare il limite per x->0, 2, ∞ delle funzioni:
3x 2−5x
x 3 −64
f  x =
f  x =
2
32  x−2
4− x
2) Calcolare il limite per x->-1, 0, 1, ∞ della funzione
2x 3 x 2 −x
f  x =
x 3 1
3) Calcolare il limite per x->-2, 0, 2, ∞ della funzione
f  x =  x 2 5− x
11
Studio di funzioni
Usiamo come esempio la funzione:
f  x =
axb ℝ
cxd
1) Determinare il campo di esistenza
Nel nostro caso: ℝ escluso x=-d/c
2) Determinare il comportamento all'infinito:
a
lim f  x =
c
x ∞
3) Determinare i possibili asintoti verticali (o orizzontali)
lim f  x=∞
x
−d
c
4) Intersezioni con gli assi
- Si pone x=0 f(x)=b/d e' l'ordinata del punto di intersezione con
Asse y, se b=0 l'intersezione e' l'origine.
- Si pone f(x)=0 x=-b/a, ascissa del punto di intersezione con
l'asse x
12
5) Determinare di massimi e/o minimi
Questo lo faremo studiando la derivata della funzione
6) Disegnare il grafico della funzione
x=-d/c
y=b/d
Asintoto
orizzontale
y=a/c
x=-b/a
Asintoto
verticale
13