ALMA MATER STUDIORUM – UNIVERSITÀ DEGLI STUDI DI BOLOGNA
FACOLTÀ DI ECONOMIA – CORSO DI LAUREA IN ECONOMIA E MARKETING
INSEGNAMENTO DI ANALISI DI MERCATO – A.A. 2009-2010
ESEMPIO DI PROVA D’ESAME
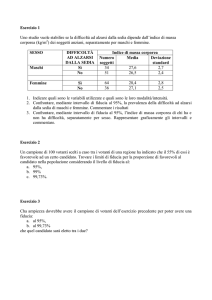
ESERCIZIO 9
Un’indagine sulla customer satisfaction ha prodotto il
seguente intervallo di confidenza al 99% per la stima della
frequenza di clienti soddisfatti di un servizio:
[64% ; 76%]
Di quanti clienti era costituito il campione, sapendo che è
stato estratto con criterio casuale semplice con ripetizione
da una popolazione molto numerosa? (6pt.).
Soluzione
p* = 70%
θ = 6%
z/2 = 2,58
Formula da usare
n = [p*(1-p)*(z/2)2]/(θ)2
((0,70 x 0,30) x (2,58) 2)/ (0,06) 2 = 388
ESERCIZIO 2
L’Agenzia delle Entrate della Provincia di Bologna vuole
stimare l’ammontare medio delle detrazioni per
ristrutturazioni edilizie dichiarate dai contribuenti residenti
a Bologna nel 2008.
Le dichiarazioni presentate nel 2008 sono state 115.000.
L’Agenzia vuole ottenere una stima con = 0,95 e con una
precisione pari a 200 euro.
Da un’analisi preliminare lo scarto quadratico medio nella
popolazione è circa pari a 800 euro.
Soluzione
= 800
θ = 100
z/2 = 1,96
Formula da usare
n = [ (z/2)2]/(θ)2
n = [800 (1,96)2]/(100)2
n = 246
ESERCIZIO 3
L’Ufficio scolastico di Bologna intende compiere
un’indagine per accertare quale è la percentuale di studenti
iscritti alle scuole superiori della provincia che ha nella
propria abitazione una connessione a banda larga.
Gli iscritti a tutti i cinue anni di corso sono
complessivamente nella provincia 35.000.
Si decide di segmentare la popolazione in tre strati (licei,
istituti tecnici, istituti professionali) e di eseguire un
campione stratificato. Determinate la numerosità
campionaria e la numerosità in ciascun strato.
Soluzione
Si decide di ottenere una precisione complessiva della
stima, (con = 0,95) pari allo 0,03%.
Poiché siamo in condizioni di completa ignoranza sulle
diverse percentuali all’interno dei tre strati, assumiamo he
siano uguali e pari a = 0,50.
Pesi
Strato 1 (licei) = 0,45
Strato 2 (ist, tecnici) = 0,35
Strato 3 (ist. professionali) = 0,20
Riepilogando:
p1 = p2 = p3 = p = 0,50
z /2 = 1,96
1 = 2 = 3 = = (0,5 x 0,5)1/2 = 0,5
θ = 0,03
W1 = 0,45 ; W2 = 0,35 ; W3 = 0,20
Formula da usare
W
s
h h
h 1
z 2 2
L
n
2
L
1
W s
h 1
2
h h
N z 2
2
Quindi:
numeratore =
(( 0,5 x 0,45 + 0,5 x 0,35 + 0,5 x 0,20)2 / (0,03/1,96) 2 ) =
0,25 /0,00023409 = 1068
denominatore =
1 + (0,45 x 0,25 +
0,25)/35.000(0,03/1,96) 2 =
1 + 0,5 /8,19=1,061
n = 1068/1,061 = 1007.
0,35
x
0,25
+
0,20
x
Se avessimo eseguito un campione casuale semplice la
numerosità campionaria sarebbe stata data dalla formula:
n
z2 2 p(1 p)
2
n =((1,96)2 x 0,25)/ (0,03)2= 1067.
Il guadagno in numerosità derivante dall’impiego del
campionamento stratificato in questo caso è nullo. La
riduzione della numerosità campionaria è dovuta
all’impiego della formula per il campionamento in
blocco.
Si immagini ora che da informazioni a priori sia posibile
ipotizzare che le percentuali siano diverse in ciascun strato.
E precisamente:
p1 = 0,8
1=(0,8x0,2)1/2=0,4
p2 = 0,5
2=(0,5x=0,5) 1/2=0,5
p3 = 0,4
3=(0,6x0,4) 1/2=0,49
Procediamo ora al calcolo della numerosità campionaria.
numeratore =
(( 0,4 x 0,45 + 0,5 x 0,35 + 0,49 x 0,20)2 / (0,03/1,96) 2 ) =
(0,18+0,175+0,098) 2/0,00023409 = 877
denominatore =
1 + (0,45 x 0,16 +
0,24)/35.000(0,03/1,96) 2 =
0,35
x
0,25
+
0,20
x
1 + (0,2075 /8,19)=1,025
n = 877/1,025 = 856
In questo secondo caso la riduzione della numerosità
campionaria, a parità di precisione e d a, è di circa il
20%.
La allocazione del campione tra i tre strati, in questo
secondo caso, può essere fatta sia con lo schema di tipo
proporzionale che con quello di tipo ottimale.