STATISTICA corso di Laurea L-36 prof. P. Giacomello
Esempio di Compito sulla parte inferenziale (dalle probabilità in poi)
Riportare la risposta esatta sul retro del foglio
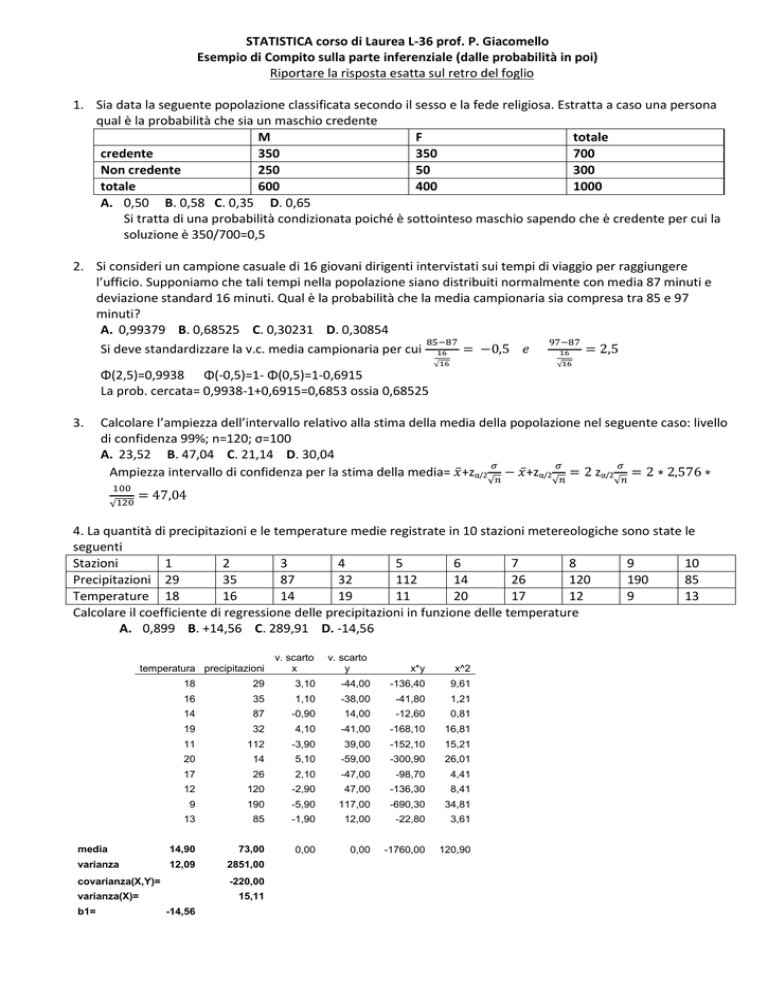
1. Sia data la seguente popolazione classificata secondo il sesso e la fede religiosa. Estratta a caso una persona
qual è la probabilità che sia un maschio credente
M
F
totale
credente
350
350
700
Non credente
250
50
300
totale
600
400
1000
A. 0,50 B. 0,58 C. 0,35 D. 0,65
Si tratta di una probabilità condizionata poiché è sottointeso maschio sapendo che è credente per cui la
soluzione è 350/700=0,5
2. Si consideri un campione casuale di 16 giovani dirigenti intervistati sui tempi di viaggio per raggiungere
l’ufficio. Supponiamo che tali tempi nella popolazione siano distribuiti normalmente con media 87 minuti e
deviazione standard 16 minuti. Qual è la probabilità che la media campionaria sia compresa tra 85 e 97
minuti?
A. 0,99379 B. 0,68525 C. 0,30231 D. 0,30854
85−87
97−87
Si deve standardizzare la v.c. media campionaria per cui 16 = −0,5 𝑒
= 2,5
16
√16
√16
Φ(2,5)=0,9938 Φ(-0,5)=1- Φ(0,5)=1-0,6915
La prob. cercata= 0,9938-1+0,6915=0,6853 ossia 0,68525
3.
Calcolare l’ampiezza dell’intervallo relativo alla stima della media della popolazione nel seguente caso: livello
di confidenza 99%; n=120; σ=100
A. 23,52 B. 47,04 C. 21,14 D. 30,04
𝜎
𝜎
𝜎
Ampiezza intervallo di confidenza per la stima della media= 𝑥̅ +zα/2 𝑛 − 𝑥̅ +zα/2 𝑛 = 2 zα/2 𝑛 = 2 ∗ 2,576 ∗
100
√120
√
√
√
= 47,04
4. La quantità di precipitazioni e le temperature medie registrate in 10 stazioni metereologiche sono state le
seguenti
Stazioni
1
2
3
4
5
6
7
8
9
10
Precipitazioni 29
35
87
32
112
14
26
120
190
85
Temperature 18
16
14
19
11
20
17
12
9
13
Calcolare il coefficiente di regressione delle precipitazioni in funzione delle temperature
A. 0,899 B. +14,56 C. 289,91 D. -14,56
temperatura precipitazioni
v. scarto
y
x*y
x^2
3,10
-44,00
-136,40
9,61
35
1,10
-38,00
-41,80
1,21
87
-0,90
14,00
-12,60
0,81
18
29
16
14
19
32
4,10
-41,00
-168,10
16,81
11
112
-3,90
39,00
-152,10
15,21
20
14
5,10
-59,00
-300,90
26,01
17
26
2,10
-47,00
-98,70
4,41
12
120
-2,90
47,00
-136,30
8,41
9
190
-5,90
117,00
-690,30
34,81
13
85
-1,90
12,00
-22,80
3,61
0,00
0,00
-1760,00
120,90
media
14,90
73,00
varianza
12,09
2851,00
covarianza(X,Y)=
-220,00
varianza(X)=
b1=
v. scarto
x
15,11
-14,56
5. Si supponga che i dati relativi alle precipitazioni dell’esercizio 4 derivino da un campione, stimare la varianza
della popolazione
A. 4150,33 B. 2851,00 C. 3167,78 D. 56,28
La stima della varianza differisce dalla varianza della popolazione per il fattore n/n-1 per la stima=
2851,00*10/9=3167,78
6. La distribuzione dello stimatore media campionaria è normale se:
A. la numerosità del campione è < 30 B. la popolazione si distribuisce normalmente
C. sempre indipendentemente da qualsiasi condizione D. mai nonostante qualsiasi condizione
7. Se lo stimatore A corretto ha varianza maggiore dello stimatore B corretto si avrà che
A. Lo stimatore A è più efficiente dello stimatore B B. Lo stimatore A è efficiente quanto lo stimatore B
C. Lo stimatore A è meno efficiente dello stimatore B D. L’efficienza degli stimatori si basa sul
confronto delle medie e non delle varianze.
8. La probabilità che una variabile casuale continua X assuma un singolo valore x0 è sempre uguale a 1 quando
A. La variabile è una Normale B la media della variabile è pari a 0 C. mai, la probabilità di una v.c.
continua in un punto non si può calcolare D. nessuna delle precedenti affermazioni
9. Il livello di confidenza nella stima intervallare è dato dalla semiampiezza dell’intervallo
A. sì se la popolazione si distribuisce normalmente B. sì se la variabile è standardizzata
C. no, viene fissato a priori D. no è dato dall’ampiezza dell’intervallo
10. Due eventi A e B sono indipendenti quando
A. la probabilità di A viene modificata dal verificarsi dell’evento B B. la probabilità di A non viene
modificata dal verificarsi dell’evento B C. l’unione dei due eventi si traduce nella somma delle
probabilità dei due eventi D. l’unione dei due eventi si trasforma nel prodotto dei due eventi












